在数值求解计算中，常常会遇到非线性方程。与线性方程相比，非线性有限元方程的建立和求解困难较大。下面结合对流扩散方程的求解，讨论非线性有限元方程的建立及其求解。

考虑一维定常的对流扩散方程

方程左端第二项反映流体的对流效应，是非线性项。

对非线性方程（3.10.1）可写出其伽辽金积分表达式

作分部积分，可得

其中，D为求解域，Γ₂为自然边界，对于一维问题D是线段，Γ₂是自然边界点。上式中用D，Γ₂表示，使表达式更具有一般性。

对求解区域D进行剖分，剖分后的单元区域为D^（e），取单元的近似解为

u（e）=N_i^（e）u_i^（e） （3.10.3）

用式（3.10.3）所表示的近似函数来代替式（3.10.2）中的u，并令

δu=N^（e）_i(www.daowen.com)

得到单元的有限元列式

A_ij^（e）u_j+B_ijk^（e）u_ju_k=f_i^（e） （3.10.4）

式中，

其中，Γ₂^（e）是e单元属于Γ₂的边界。若没有与Γ₂相联的单元，则关于这项的积分不出现，而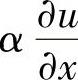由自然边界条件给出。

总体合成时，将单元结点序号的下标值转换到总体结点序号，然后将所有单元的有限元列式的各个系数按转换后的下标进行累加，即得到总体有限元方程

A_nmu_m+B_nmlu_mu_l=fn（n=1，2，…，N） （3.10.5）

其中，系数矩阵A_nm，B_nml和右端项f_n由各单元系数矩阵A_ij，B_ijk和右端项f_i按结点序号转换汇集而成。

式（3.10.5）所表示的总体有限元方程，与线性问题相比较的显著区别是出现非线性项。在进行强加边界条件处理时，一般不宜采用消行的处理方法，可采用对角线扩大法。如在第r结点上给定强加边界条件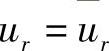，可将系数矩阵A_nm中的对角线元素A_rr乘以一个足够大的数G，如乘以G=10²⁰，使该元素成为GA_rr，同时对右端项的元素f_n乘以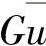，使该元素成为GuF_n，非线性项的系数矩阵B_nml仍保持不变。应用这样的方法可逐个结点处理所有强加边界条件。

经过边界条件处理之后的非线性有限元方程组，求解之后，便可以得到问题的有限元解，但求解非线性方程的主要困难是求解非线性代数方程组，非线性代数方程组的求解方法主要有两类，即线性化的方法，如牛顿法，以及求极小值的方法，如下降法。