单元分析中已经建立了单元有限元特征式，而且{A_ij^（e）}和{f_i^（e）}的各个元素的表达式也是已知的，同时，在区域剖分时已经给出了单元结点序号与总体结点序号的对应关系，每个单元的布尔矩阵{Δ_in^（e）}原则上是已知的，那么总体系数矩阵及右端项向量可以通过布尔矩阵的运算获得

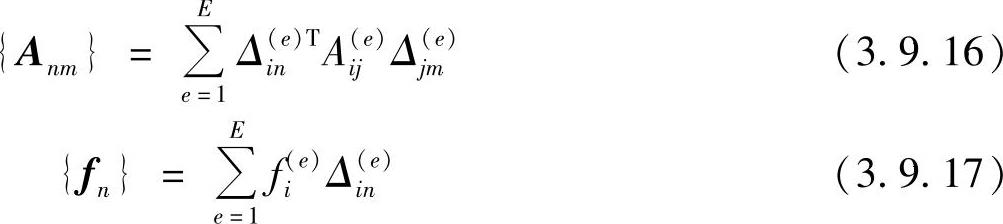
为了对上述的总体合成的过程有一个具体了解，下面以只有两个单元的简单问题加以说明。两单元问题的区域剖分如图3.9.5所示，单元结点号与总体结点号的对应关系已在图中表示清楚。

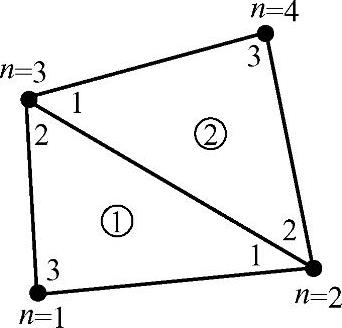
图3.9.5 两个单元的计算域

由图上结点序号的对应关系，不难获得这两个单元的布尔矩阵为

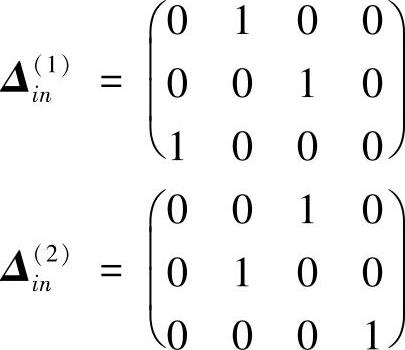(www.daowen.com)

于是可对式（3.9.16）进行具体的运算

从上述运算过程可以看出，单元有限元列式中的系数矩阵的元素下标值对应于单元结点序号，总体合成就是将这些序号转换为总体结点序号，然后把这个元素加到总体系数矩阵某个位置上去，这个位置的行列序号，正是相应的总体结点序号。例如，第一单元中的A₁₃（¹），它的下标值1和3对应于单元结点号1和3，而相应的总体结点号为2和3，因此就将A₁₃（¹）加到总体系数矩阵第2行，第3列的位置上去，即累加到A₂₃中去。当一个结点同属于两个单元时，不同单元对这个结点的相应元素都会有贡献，例如，A₂₂（¹）和A₁₁（²）按转换关系都应加到A₃₃所在的位置上去。

应当指出，在实际计算时，由于单元数量大，若要写出每一个布尔矩阵，并进行运算，将会占去大量计算机内存，耗费很多计算时间。事实上，这是完全没必要的，我们只需要将表示单元结点号与总体结点号之间关系的数据输入计算机，在进行总体合成时，由计算程序控制，逐个单元地把{A_ij（e）}中的i，j转换为相应的总体结点序号，然后再把A_ij（e）累加到总体系数矩阵相应的位置上去。