三结点三角形单元，单元基函数共有三个，可选拉格朗日线性多项式

N_i^（e）=a_i^（e）+b_i^（e）x+c_i^（e）y（i=1，2，3） （3.9.4）

若记e单元的三角形的三个顶点的坐标为（x_i^（e），y_i^（e）），（i=1，2，3），则式（3.9.3）所满足的插值条件为

φ_i^（e）（x_j^（e），y_j^（e））=δ_ij

将上式中的j分别取i，j，k，则式（3.9.4）为

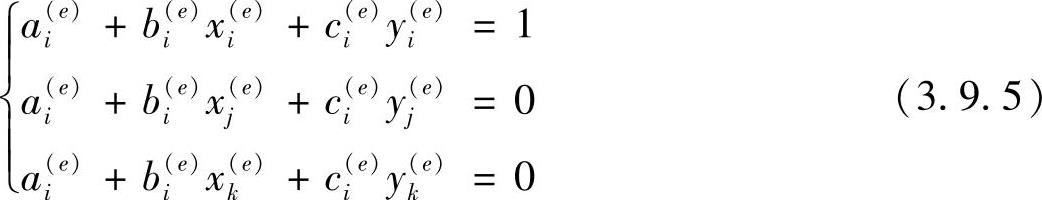
其中，下标i，j，k为单元结点号，按1，2，3的顺序循环取值。式（3.9.5）共有9个代数方程，可唯一确定a_i^（e），b_i^（e），c_i^（e），（i=1，2，3），共9个系数。求解式（3.9.5），可得

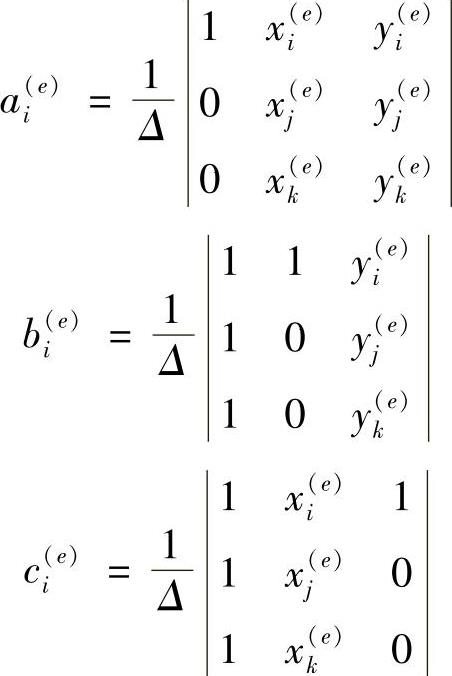
其中，

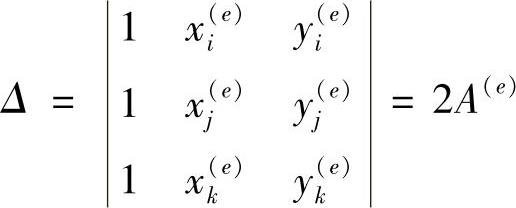
A^（e）是e单元三角形的面积，表达式为(www.daowen.com)

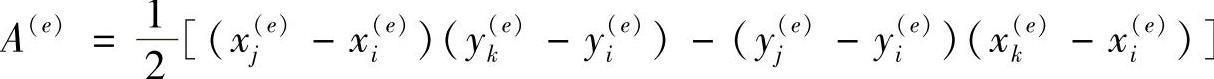
上述各式中的下标i，j，k为单元结点号，均按1，2，3的顺序循环取值。于是，得e单元中的近似函数为

u^（e）=u_i^（e）N_i^（e） （3.9.6）

将式（3.9.5）代入式（3.9.6），得

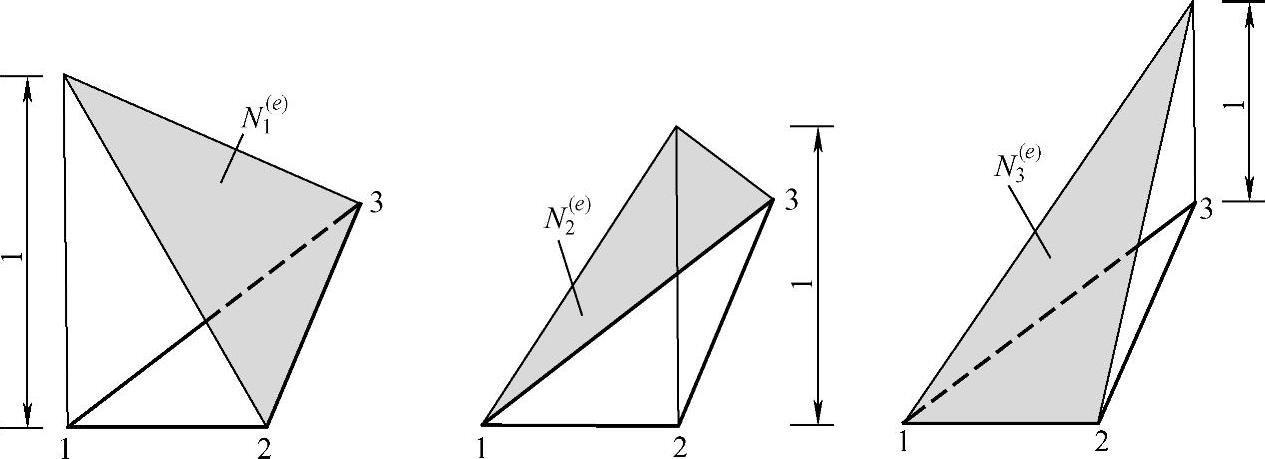
图3.9.2 三角形单元的线性基函数

三角形单元的线性基函数N_i^（e）（x，y）如图3.9.2所示，其形状是一个直角四面体的三角形斜面，单元的结点i处的函数值为1，其余两个结点j和k处的函数值为零。

全区域的基函数，可由各个基函数叠加组成。不难看出，对于区域内结点所对应的基函数是一个由若干三角形斜面所组成的尖顶形多面体的侧表面，如图3.9.3所示。