将区域D划分成E个三角形单元，并选三角形的顶点为结点。物理量变化剧烈的地方，单元划分得细一些。边界Γ₁和Γ₂可用三角形的直线边近似代替，如图3.9.1所示。单元区域记为D^（e）（e=1，2，…，E）。设全区域共有N个结点，位于强加边界Γ₁上的结点共有r个，序号为n₁，n₂，…，n_r，位于自然边界Γ₂上的结点共有s个，序号为m₁，m₂，…，m_s。总体结点序号的起点可以任意取，结点序号的排列顺序原则上没有限制，不过为了使最后总有限元方程的系数矩阵的带宽较小，一般应尽量使单元中的结点序号相差小一些。每个单元中的结点号统一按照逆时针方向排列。

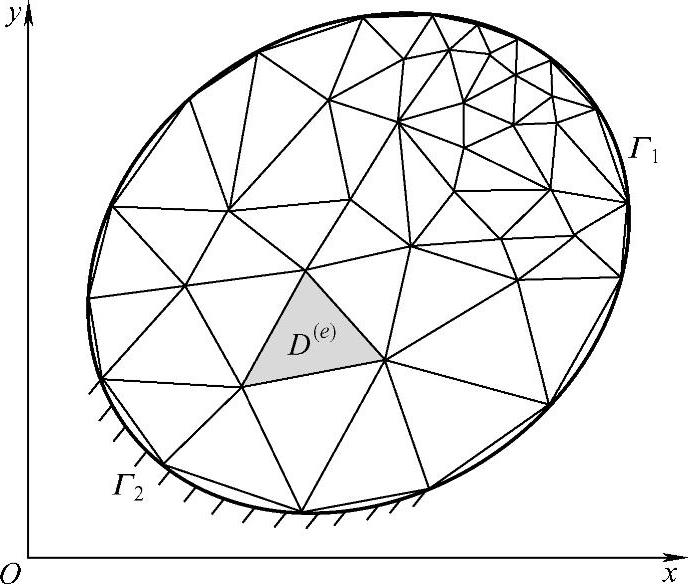
图3.9.1 二维有限元区域剖分

各个单元中的单元结点号与总体结点号的关系可先在剖分图上标清楚，然后以表格列出，同时还应分别列出所有结点坐标值的数据表、强加边界结点的函数值数据表、自然边界结点的边界值的数据表，这些工作必不可少。

采用有限元方法求解偏微分方程近似解还离不开网格生成技术。有限元单元网格的质量将直接影响计算结果的稳定性与精度，拓扑结构简单且能使定解问题的边界条件得以简单实现是对单元网格的基本要求。我们知道，有限元法需要输入大量的数据，包括结点坐标、单元联结信息和边界条件等。对于一个实际问题而言，离散模型的数据文件十分庞大，数据输入工作必然要耗费很多时间，并且非常容易出错，输入数据的精度也不足。采用网格生成技术可以避免人工逐点输入结点坐标和单元联结信息，而只需要给出少量的几何计算域及网格数据就可以得到它们。(www.daowen.com)

有限元网格生成的方法主要有合成函数法和等参变换法。采用等参变换法需要进行坐标变换，坐标变换公式为

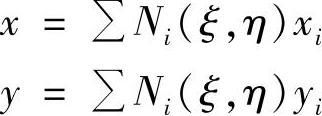
母单元中划分等间距或非等间距的网格，在子单元中就可以生成有限单元计算网格。对于平面问题，一般采用8结点等参单元进行坐标变换，对于空间问题，需采用20结点等参单元进行坐标变换。在网格生成过程中，第一步是采用高次等参单元将整个计算域划分成一些互不重叠的子区域，每个子区域看成是一个高阶等参单元，这样可以减少曲边边界的离散误差；第二步是通过线性插值，对每个子区域进行网格加密，得到大小不同的等参单元。子区域是非常粗糙和非结构化的，这样仅需要输入很少的数据信息来概略地描述整个计算域，同时这种方法可任意地控制网格结点的疏密分布。特别指出，在区域网格加密过程中应尽可能做到平滑过渡，因为随意突变的网格间距会影响计算精度和稳定性。单元网格自动生成，虽然减少了大量的数据准备时间并降低了出错几率，但网格自动生成所得到的是结点坐标和单元联结的数字信息，对它们仍然需要进行检查，核实无误后方可执行后续计算，这部分工作较繁琐和费时。