有限元法的边界条件处理极其重要，对于总体有限元方程式（3.8.13）来说，若不引进边界条件，则所得的解完全没有意义。自然边界条件一般已在积分表达式中得到满足，而强加边界条件在区域剖分时，已经标出所有位于强加边界上的结点序号以及相应的函数值或其导数值。我们可根据这些数据，对总体有限元方程进行修正，使得经修正后的总体有限元方程所获得的解满足强加边界条件。下面介绍针对强加边界条件对总体有限元方程进行修正的一般方法，然后进行具体的说明。

假定第r号结点是强加边界上的结点，边界值为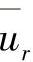。对总体有限元方程式（3.8.12）中的{A_nm}及{f_n}修正方法如下：将系数矩阵{A_nm}中相应r的对角线元素A_rr用1来代替，并将它所在的行与列，即第r行与第r列中的其余所有元素置于零，记这样的矩阵为{A_n∗_m}，称为修正的系数矩阵。同时将{f_n}中的第r行元素，改写为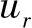，其余的各个元素f_n均减去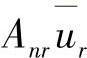，即把f_n改写为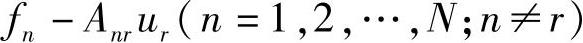。修正后的系数矩阵及右端项向量分别为

若强加边界上有两个以上的结点，则按上述方法逐个进行修正，这个方法称为消行修正法。消行修正法实质上是强制给定边界上的函数值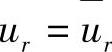，之后对方程中进行移项处理，它的正确性是十分明显的。按此想法，还有另外一种处理方法，就是将已给出了的强加边界值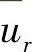的所在行、列的全部元素去掉，形成下列系数矩阵与右端项向量(www.daowen.com)

如有两个以上的强加边界结点，则按上述规则进行逐个进行修正。这个方法可使矩阵的阶数减小，尤其在强加边界结点数量较大时，对于计算内存的节省是很明显的。当然，缩减后的矩阵，原先的下标序号已经打乱，应重新编号，这在计算程序上将增加复杂性，此方法一般称为消行重新编号修正法。下面采用这种消行修正法，对式（3.8.13）中的系数矩阵及右端项向量进行修正。由边界条件可知，u₁=u₅=0，于是

修正后的总体有限元方程为