任取e单元作为讨论基函数选取的典型单元。记e单元中的基函数为

{N_i^（e）}

记单元中的近似函数为

u^（e）=u_i^（e）N_i^（e）（u_i^（e）是待定系数）

构造单元基函数{N_i^（e）}应使u_i^（e）正好是相应结点上的函数值，且每个结点分别对应一个基函数。若单元e中有I个结点，则应有I个单元基函数N_i^（e）（i=1，2，…，I）。本例题中，线段单元有两个结点，单元e有两个自由度，基函数有两个，即

N_i^（e） （i=1，2）

根据拉格朗日基函数需满足的条件

N_i^（e）（p_j）=δ_ij（i，j=1，2）

其中，p_j是单元结点序号为j的结点。于是得到本例中，基函数的插值条件为

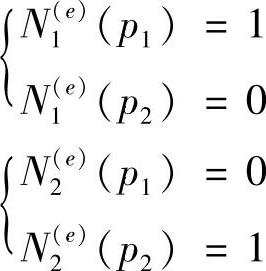
按上述原则构造的基函数，保证了近似函数中的待定系数正好是函数在结点上的值。我们根据单元中的结点数目、结点坐标以及插值条件，并假定基函数是多项式函数，就可完全确定N_i（^e）。本例中，单元中有2个结点，将选取2个基函数N₁^（e）和N₂^（e），假定基函数是多项式函数，则根据插值的条件，它必定是线性多项式

N_i^（e）=a_i^（e）+b_i^（e）x（i=1，2）

应满足

N_i^（e）（x_j^（e））=a_i^（e）+b_i^（e）x_j^（e）=δ_ij（i，j=1，2）

其中，x_j^（e）是单元e中第j号结点的坐标。不难解得

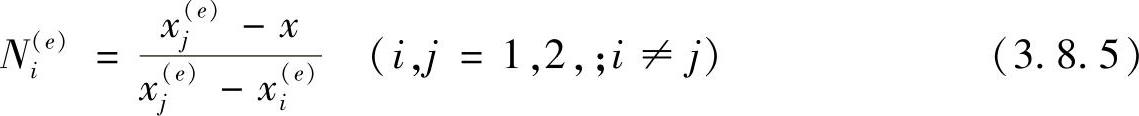
于是得单元e中近似函数的表达式为

其中，Δh=x₂^（e）-x₁^（e）。(www.daowen.com)

引进无量纲自然坐标

则有

在自然坐标中，单元中序号为1，2的结点的坐标值分别为ξ=0，ξ=1，将其代入式（3.8.6）中，可以看到，单元基函数的函数值在相应结点上的值为1，其余结点0，单元中近似函数的系数正是相应结点上的函数值。

全域的基函数可看做所有单元基函数的总和，每个结点相应有一个基函数。由于一个结点可能分属于若干单元，因此这个结点的基函数将是它所分属的单元中相应基函数的叠加。若全区域中的基函数记为

{N_n}（n=1，2，…，N）

则根据u_n=Δ_in^（e）u_i^（e）的表示方法，有

全域的近似函数可以表示为

又根据u_i^（e）=Δ_in^（e）u_n的转换关系，上式可写成

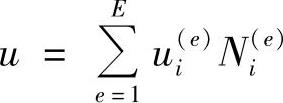
可见，全区域的近似函数是各个单元中的近似函数的叠加。在本例题中，将式（3.8.5）进行叠加求和，即可获得总体基函数。相应结点序号为n的总体基函数可表示为

上述表达式适用于n=2，3，4的内部结点所对应的基函数。当n=1，5时，边界结点所对应的基函数只需将无定义的边界外区域去掉即可。内部结点所对应的基函数如图3.8.2所示。它是“尖顶形”的函数，在相应结点上的值为1，其他结点的值都为0，相邻结点间呈线性变化。

图3.8.2 一维线性基函数