1.协调问题和拟协调单元

等参单元只能保证单元之间插值函数本身的连续性，它只适用于只含待定函数及其一阶导数的变分问题。为了满足近似函数的协调条件，一般要采用埃尔米特插值多项式。埃尔米特插值多项式按结点导数的最高阶次，分为一阶插值，二阶插值，……对于含有高阶导数的变分问题，按照问题的协调条件，对插值函数往往要求在整个区域内有一阶的连续性，这就要求单元结点参数值包含待定函数的有关导数，这一类含有导数参数值的单元称为拟协调单元。对于拟协调单元，设单元内的结点参数包含有待定函数u=u（x，y，z）及其有关导数

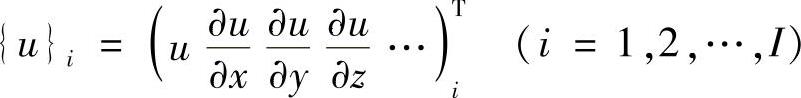
其中，I为单元的结点数。若结点参数值只取到一阶导数，则对于三维问题，每个单元有4I个结点参数值，对于二维和一维的问题，每个单元的分别有3I和2I个结点参数值。

2.二结点单元

对于零阶插值，因不含结点的导数值，埃尔米特插值多项式与拉格朗日插值多项式完全等价，这里不再赘述。

对于一阶插值，每个结点具有2个自由度，单元的自由度为4，埃尔米特插值多项式应为三次多项式

H_ki=a_ki+a_kiξ+a_kiξ²+a_kiξ³ （3.6.1）

其中，结点序号指标i=1，2；导数阶次指标k=1，2；ξ为无量纲局部坐标。

根据埃尔米特插值多项式插值条件，有

其中，j=1，2，对每一个H_ki（k，i=1，2）都有4个插值条件。将式（3.6.1）所表示的含有4个未知数的三次多项式H₀₁，H₀₂代入式（3.6.2），H₁₁、H₁₂代入式（3.6.3）时，即分别形成4个封闭的代数方程组，求解该方程组，就可获得各个埃尔米特插值多项式

这些插值多项式如图3.6.1所示。

可以看到，采用一阶埃尔米特插值多项式作为单元基函数时，每个结点对应有两个基函数，二结点的单元中共有四个基函数，这是与拉格朗日插值多项式作为基函数时的一个重要不同点。

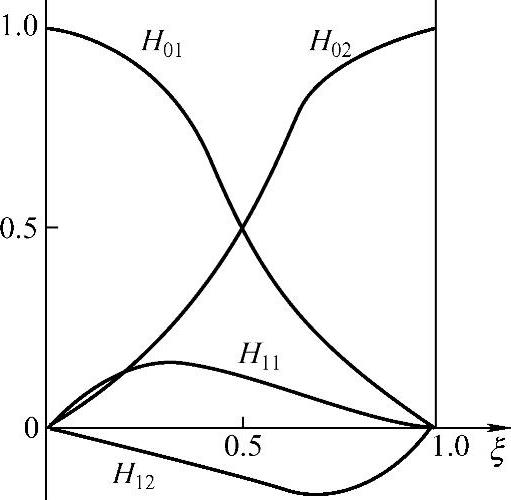
图3.6.1 两点一阶埃尔来特插值多项式

当采用二阶埃尔米特插值多项式作为基函数时，每个结点具有3个自由度，单元的自由度为6，埃尔米特插值多项式应为五次多项式，根据埃尔米特插值多项式插值条件，有

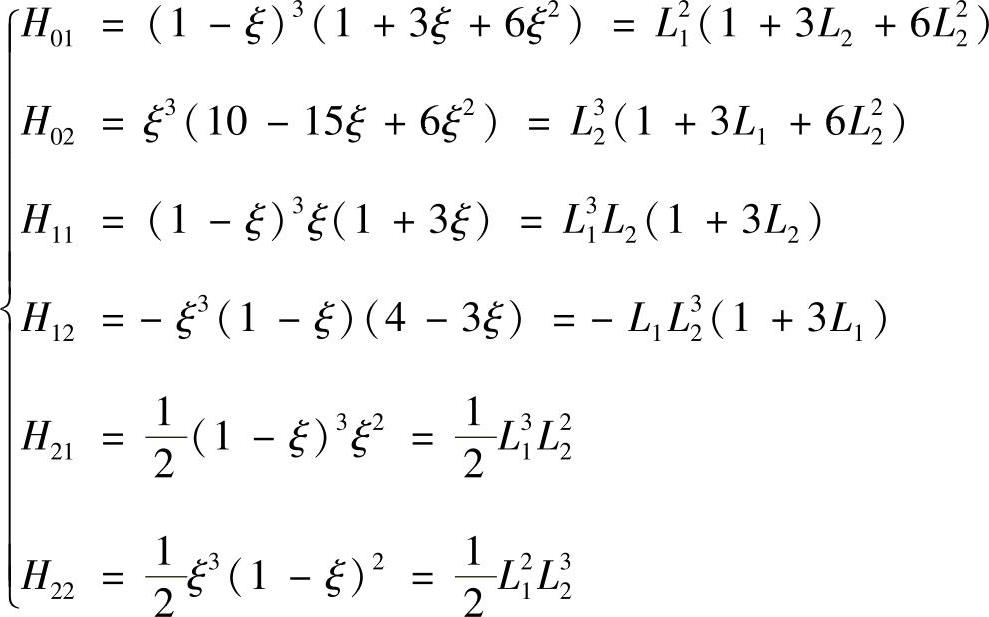
近似函数表达式为

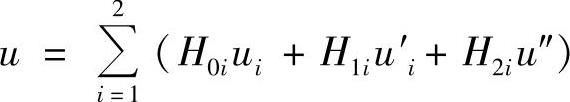
广义坐标不仅有结点的函数值，而且有结点上函数的一阶和二阶导数值。对于更高阶次的插值，或多结点的埃尔米特多项式，也可完全仿照上述方法确定，一般地，对于高次插值多项式，单元中的结点应尽量减少。

3.三角形单元的埃尔米特插值函数

当结点函数值及其一阶导数被作为结点参数值时，每个结点具有3个自由度，三结点三角形单元具有9个自由度，而根据帕斯卡三角形，完整的三次多项式总共有10项，为了使单元的自由度个数与多项式项数一致，有两条途径，一是在三次多项式中减少一项，但这样将破坏多项式的完整性和对称性，应尽力避免；二是在单元中增加一个自由度。我们选择后一条途径，为此，在三角形的形心上增加一个结点，这个结点只取函数值作为结点参考值，具有一个自由度。三角形的结点序号与面积坐标值如图3.6.2所示。

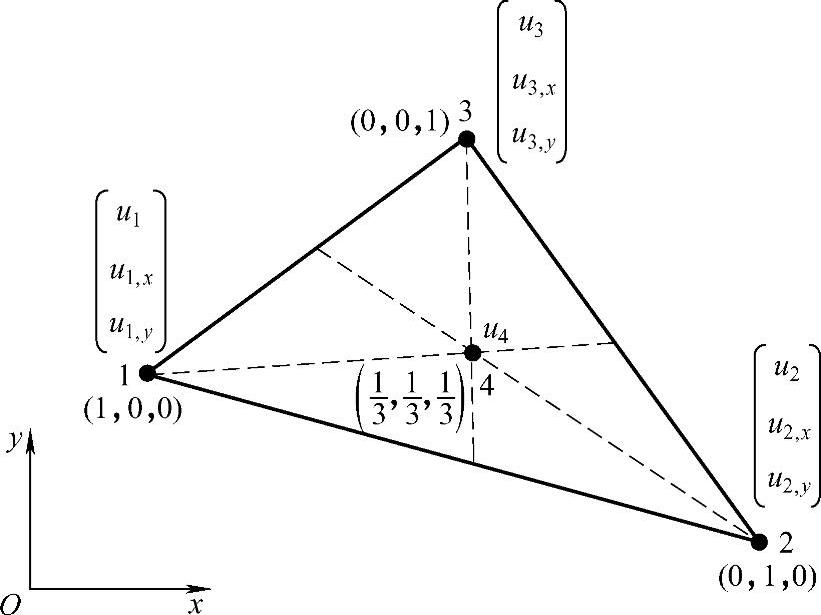
图3.6.2 以函数及其导数为结点参数的三角形单元

完整的三次多项式含有10个系数，一般可表示为

H_i=α_1i+α_2iL₁+α_3iL₂+α_4iL²₁+α_5iL₁L₂+α_6iL²₂+α_7iL₁L²₂+α_8iL²₁L₂+α_9iL³₁+α_10iL₂³ （3.6.4）

近似函数的表达式为

u=H₁u₁+H₂u_1，x+H₃u_1，y+H₄u₂+H₅u_2，x+H₆u_2，y+H₇u₃+H₈u_3，x+H₉u_3，y+H₁₀u₄

其中，待定系数u_i是序号为i的结点上的近似函数值，u_i，x和u_i，y是近似函数在序号为i的结点上的偏导数值

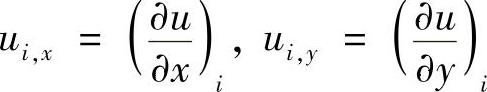
于是，各个插值函数H_i=H_i（x，y）应满足的插值条件为

当i=1，4，7，10时，有

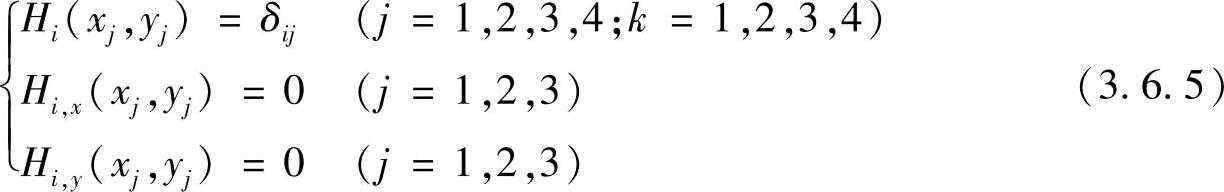
当i=2，5，8时，有(www.daowen.com)

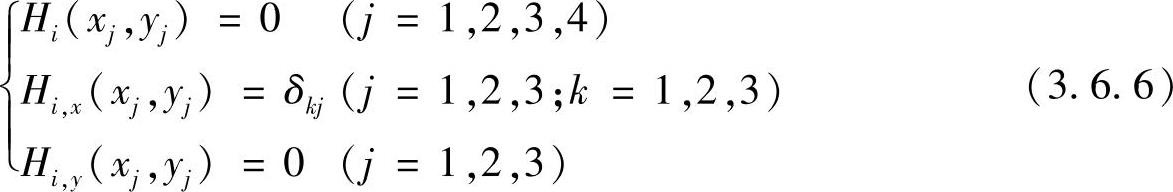
当i=3，6，9时，有

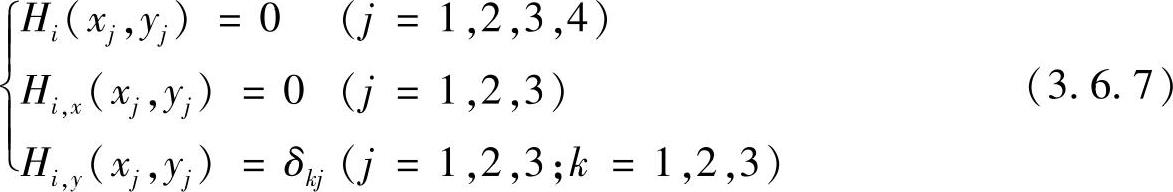
式中，

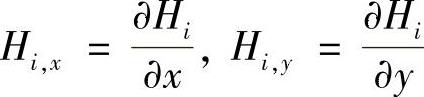
按照上述各个插值条件，每个插值函数都应有10个插值条件，因此，只要将式（3.6.4）代入相应的插值表达式（3.6.5），式（3.6.6）和式（3.6.7）中，并注意到下列直角坐标系与面积坐标系取导数的关系

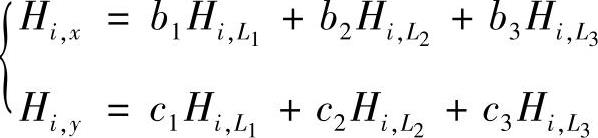
其中，b_k，c_k（k=1，2，3）按照式（3.3.14）计算。

这样就可以建立10组含有α_1i，α_2i，…，α_10i（i=1，2，…，10）的线性代数方程组，解出各组系数，代回式（3.6.4），即可得到下列三角形单元的埃尔米特插值函数

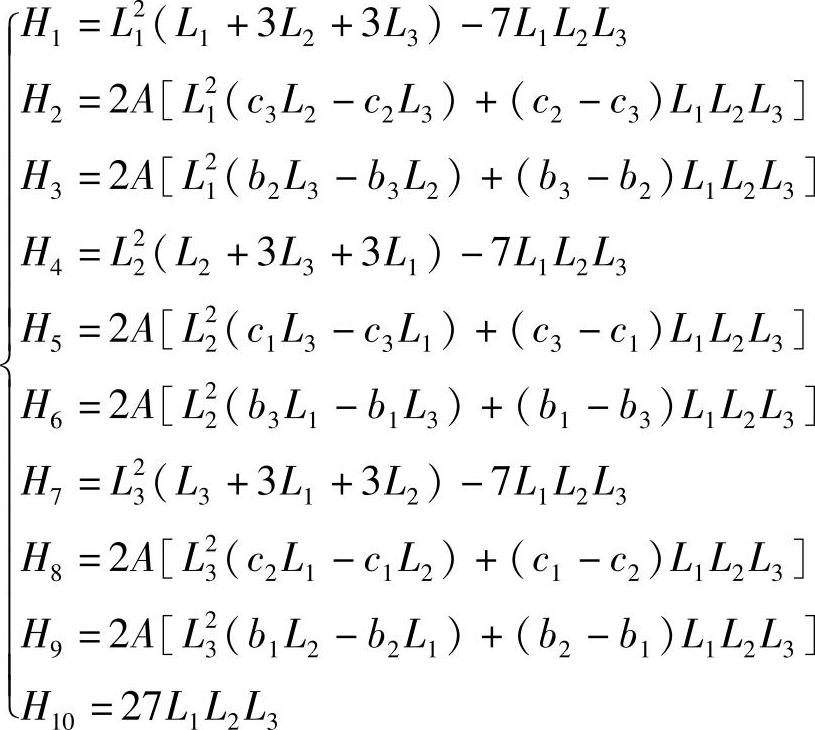
其中，A为三角形面积，由式（3.3.15），可得

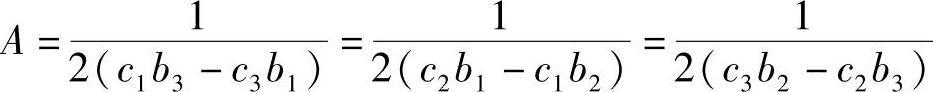
4.矩形单元的埃尔米特插值函数

四结点矩形单元中，当结点参数取函数值及其导数值时，将具有12个自由度，此时单元中的近似函数为

u=H₁u₁+H₂u_1，x+H₃u_1，y+H₄u₂+H₅u_2，x+H₆u_2，y+H₇u₃+H₈u_3，x+H₉u_3，y+H₁₀u₄+H₁₁u_4，x+H₁₂u_4，y

下面给出各个基函数应该满足的插值条件。

当i=1，4，7，10时，有

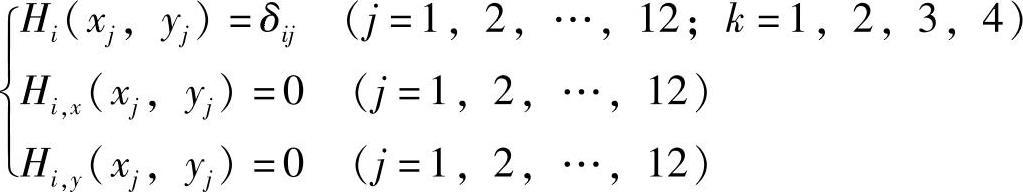
当i=2，5，8时，有

当i=3，6，9时，有

由于单元有12个自由度，因此埃尔米特插值多项式有12项，这可以在完整的三次多项式中再增加2个对称项来构成

H_i=α_1i+α_2iξ+α_3iη+α_4iξ²+α_5iξη+α_6iη²+α_7iξη²+α_8iξ²η+α_9iξ³+α_10iη³+α_11iξ³η+α_12iξη³ （3.6.8）

式中的无量纲局部坐标ξ，η和直角坐标x，y的关系为

式中，（x₁，y₁）是结点1的坐标，a和b分别为矩形的宽和高。各结点的位置与序号如图3.6.3所示。

根据式（3.6.9），有导数间的关系

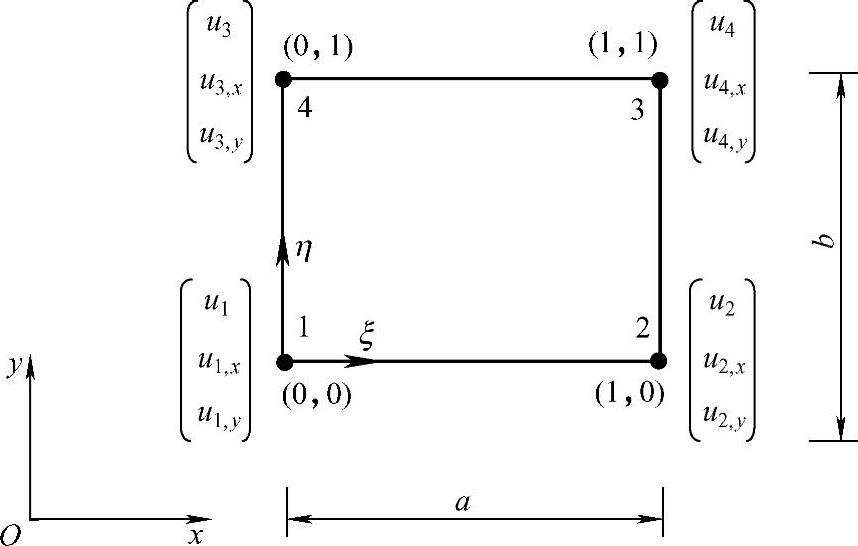
图3.6.3 函数及其导数为结点参数的矩形单元

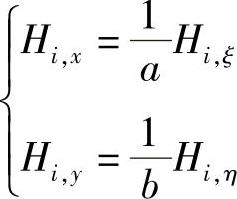
将式（3.6.8）所表示的插值函数，按其结点序号下标i，分别代入各个相应的插值条件式，并利用两坐标系下导数间关系，则可分别建立以α_1i，α_2i，…，α_12i诸系数为未知量的线性代数方程组，解出各系数后，即可获得下列所示的四结点矩形单元埃尔米特插值多项式

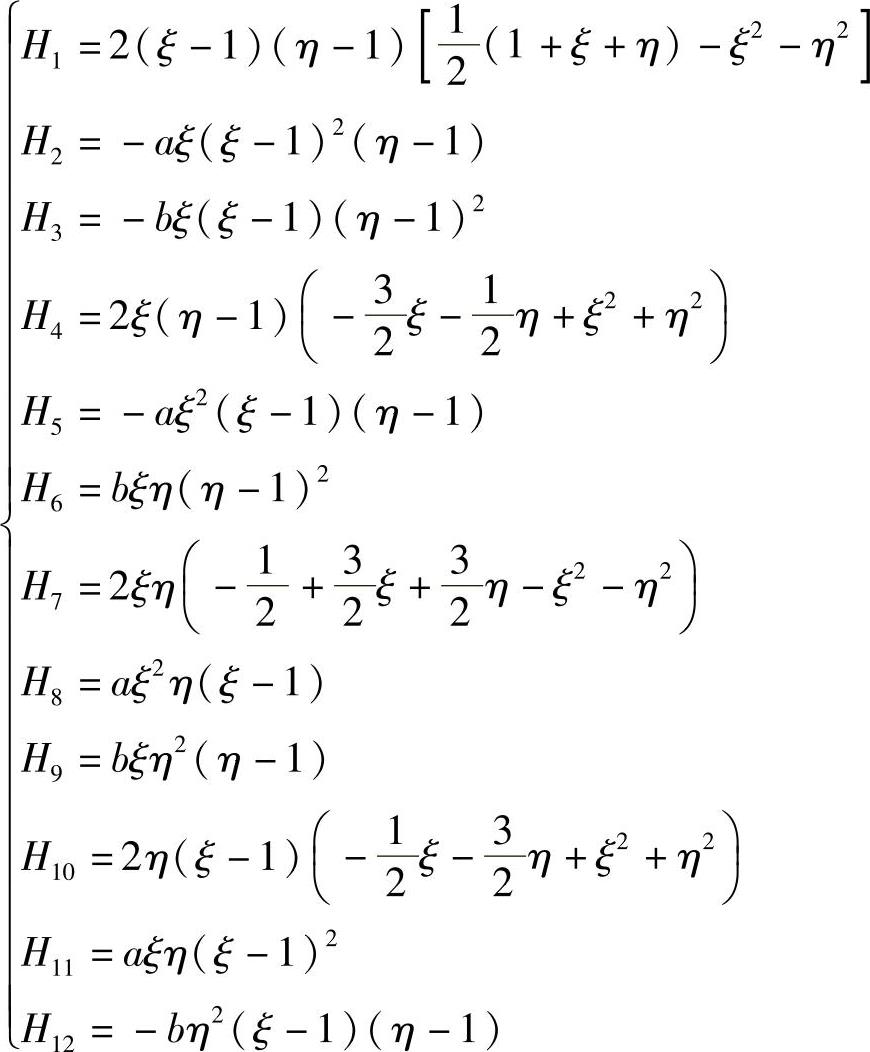
前面讨论了拉格朗日插值和埃尔米特插值，我们只要采用结点坐标插值形式的坐标变换，就可以把xOy平面上的单元映射为局部坐标系中的规则单元，函数u的插值可以与坐标变换的插值函数相同，即构成所谓等参单元，也可以完全不同，取高阶或低阶次的插值函数，甚至是埃尔米特插值函数。事实上，等参单元只是曲边单元中的一种特殊情况，且只能用于拉格朗日插值，仅从提高单元的几何表现能力而言，也不必一定用等参单元。

一般讲，采用基本单元与线性插值具有计算简便等优点，但其计算精度较差。为了满足计算精度的要求，常要加密单元的划分，这样将增加计算的工作量。如采用高次插值单元，其计算精度较髙，但计算较复杂，计算所需机时较多。二次单元是经常采用的计算单元，因其计算工作量增加不多，还可满足较高计算精度的要求。