以上介绍了二维问题中的三角形单元和矩形单元，三角形单元剖分简便灵活，是常用的方法，但是如果只是作线性插值，对于需要计算导数的问题其精确度较差。用矩形单元作剖分，如果要计算导数，它的效果比三角形单元剖分要好些，但若对任意区域作矩形剖分，显然适应性要差些，因此可以考虑把两者结合起来，希望具有两者的优点。此外，对于任意区域来说，不论是三角形剖分还是矩形剖分，都需要用直线段代替曲线边界来得到近似区域，有时人们会不满意这种近似，如果采用曲线边界的单元则会得到更好的近似区域，基于以上考虑，引入等参单元的概念。

对于二维问题来说，通常的曲线单元有曲线三角形单元和曲线四边形单元，而任意直边三角形和任意直边四边形单元可作为曲线单元的特例。事实上，只要采用插值函数展开形式的坐标变换关系，就可以把xOy平面上的曲边单元映射成局部坐标系中的直边单元。在曲边单元内，近似解u的插值函数展开可用拉格朗日插值，也可用埃尔米特插值，可用线性插值，也可用高次插值，一般来说，并不要求函数的插值形式与坐标变换的插值形式相同。

1.等参单元及其应用特点

等参数单元具有两个特性：

一是每个待定的函数u在每个结点i上只有一个参数值u_i。如将结点坐标值x_i看做坐标变量x在结点上的参数值，则单元上每个待定函数和坐标变量的结点参数值个数相同，且等于单元的结点数。

二是单元内的变点P的坐标与近似函数各分量同结点参数值具有统一的线性关系，即

式中，N_i为以局部坐标为变量的形函数；Q表示P的整体坐标或近似函数各分量；Q_i为对应的结点参数值。

上一节所讨论的基本单元就是一类最简单的等参单元，式（3.5.1）就是式（3.4.6）和式（3.4.7）两式的统一形式。

为了提高计算精度，需要对待定函数作高次插值，这就需要在基本单元的基础上增加单元的结点，等参单元适合高次插值，单元又可以是曲边形的，因而在有限元分析中常被采用。等参单元具有下面的应用特点：

第一，采用等参单元可以增加插值的次数，提高计算的精度。高次等参单元的边界可取曲线或曲面，因此能适应计算域边界的弯曲特性。等参单元在构造形函数时采用自然坐标，并取局部坐标中母单元统一形式的形函数。对于直角坐标中各任意形状的子单元，通过它和母单元之间的对应关系进行变换计算，在计算过程中不必考虑单元边界的形状。等参单元的边界是由不同阶次的曲线或两族曲线组成的曲面所构成，单元的形状完全由结点的数目及其坐标（x_i，y_i，z_i）确定。因此，在划分等参单元时，弯曲边界上的结点可根据边界几何形状来布置，但对内部结点的布置则应尽量平直，以便于计算。

第二，等参单元之间关于坐标变换的相容性和插值函数的连续性是等价的，根据式（3.5.1），若边界上结点参数值个数和插值多项式项数相等，则两相邻单元的插值函数在公共边界上的值由公共结点参数唯一确定，这样就保证了边界的连续性。同时公共边界上坐标的参数表达式也由该公共结点的坐标值确定，也保证了坐标变换在边界上的相容性。

第三，完全的m元或（m+1）元n次多项式的项数为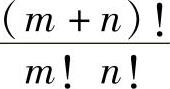，用此式可以判断相容条件是否满足、n次插值是否完全以及边界结点的分布是否合理。不完全的髙次插值对解的收敛性一般是不利的，但九结点三角形单元、二十结点六面体单元的插值只在三次以上作调整，对二次多项式是准确的。

常用的等参单元有一维的多结点线段单元，二维的六结点和九、十结点三角形单元，八、九结点四边形单元，三维的十结点和二十结点四面体单元，二十结点六面体单元等。

2.多结点线段单元

取单元的形函数为二次拉格朗日插值多项式

N_i=a_i+b_ix+c_ix² （3.5.2）

此时，为了唯一确定插值多项式（3.5.2）中的系数，需在线段单元中设置3个结点，一般取单元的中点为第3个结点，如图3.5.1所示。设结点1，2，3的坐标分别为x₁，x₂，x₃，利用插值条件

N_i（x_j）=δ_ij（i，j=1，2，3）

解出式（3.5.2）中的系数

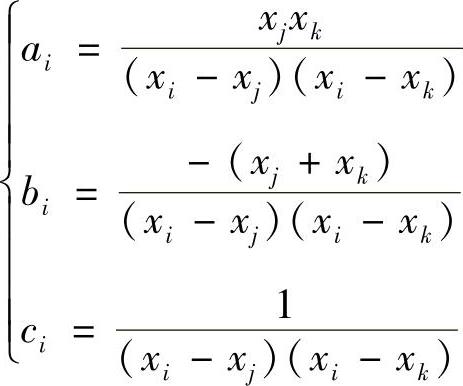
上式中指标i，j，k按1，2，3的顺序循环取值，于是，得

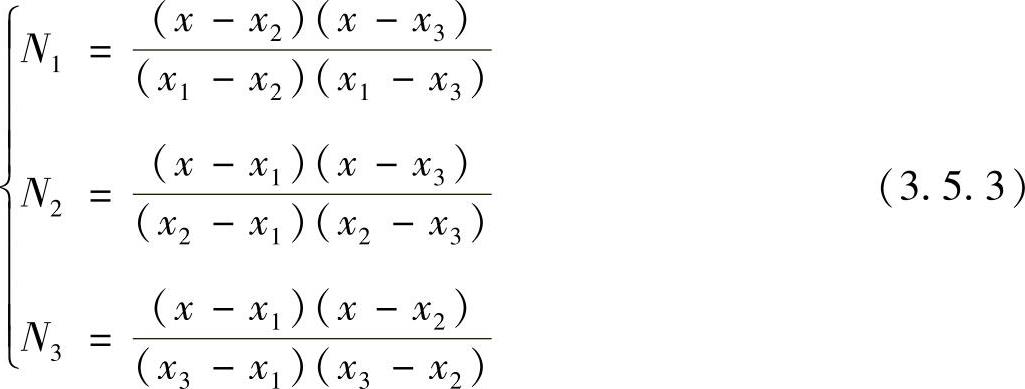
如取长度等于2的直线段母单元，如图3.3.5所示，对无量纲局部坐标作变换

单元三个结点的局部坐标分别为ξ₁=-1，ξ₂=1，ξ₃=0，用局部坐标表示的插值函数为

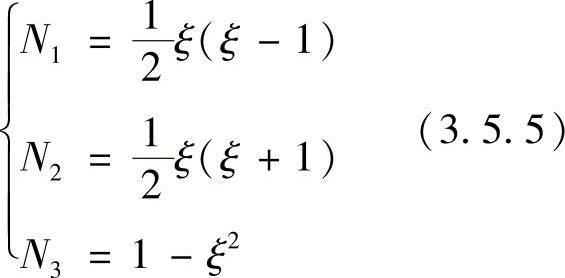
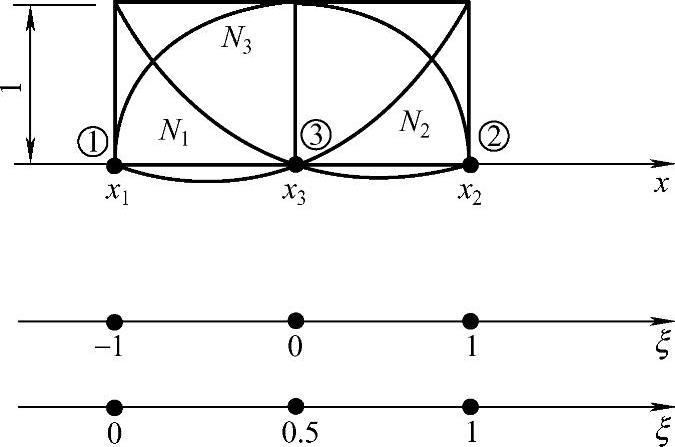
图3.5.1 三结点线段单元二次插值

此时，三结点线段单元的近似函数为

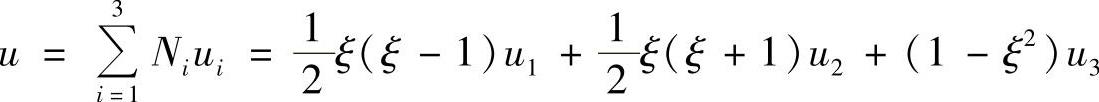
如取长度等于1的直线段母单元，如图3.3.4所示，对无量纲局部坐标作变换

这时单元三个结点的局部坐标分别为ξ₁=0，ξ₂=1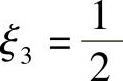，，插值函数为

若采用r次插值多项式作为单元形函数，则在单元中要设置r+1个结点。例如，四结点线段单元取线段的两个三分点为第3、第4结点，单元的自由度为4，采用三次拉格朗日插值多项式。不难推出r次插值多项式的插值函数为

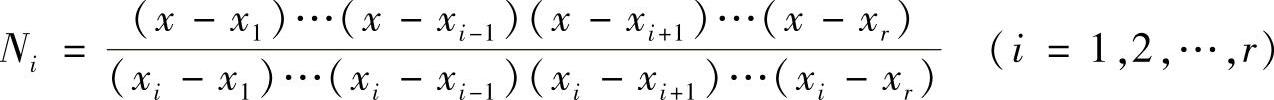
其中，x_i为单元第i个结点坐标。单元的近似函数可按式（3.5.1）给出表达式。

3.六结点以及九结点和十结点三角形单元

为了提高精度，可以增加单元数目，也可以在单元中增加结点，采用高次插值多项式作为基函数。常用的高次插值多项式是二次多项式与三次多项式。六结点三角形单元除三个顶点外，再增设三条边线的中点，它们的序号及面积坐标值如图3.5.2所示。

采用二次拉格朗日插值多项式，完整的二次多项式有6项，有6个系数，由6个结点来确定。在帕斯卡三角形中，取6项的完整二次多项式，其用面积坐标表示为

N_i=a_1i+a_2iL₁+a_3iL₂+a_4iL²₁+a_5iL²₂+a_6iL₁L₂ （3.5.8）

或

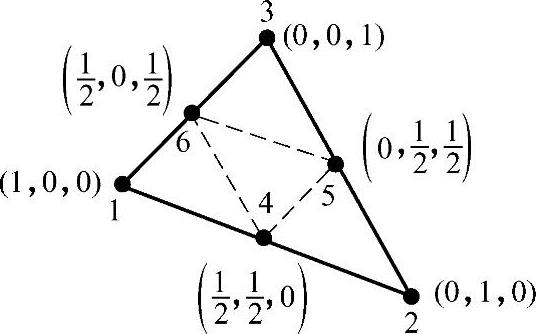
图3.5.2 六结点三角形单元

N_i=a_1i+a_2iL₁+a_3iL₂+a_4iL₁L₂+a_5iL₂L₃+a_6iL₃L₁ （3.5.9）

上述表达式中的各个系数，可以根据插值条件

N_i（L_1，j，L_2，j，L_3，j）=δij（i，j=1，2，…，6） （3.5.10）

确定。只需将三角形单元中的如图3.5.2所示的六个结点的面积坐标值L_1，j，L_2，j，L_3，j（j=1，2，…，6），代入式（3.5.8）或式（3.5.9）中，并按条件式（3.5.10），即可建立6个含有a_1i，a_1i，…，a_6i的线性代数方程组。求出插值多项式的各组系数，则插值函数为

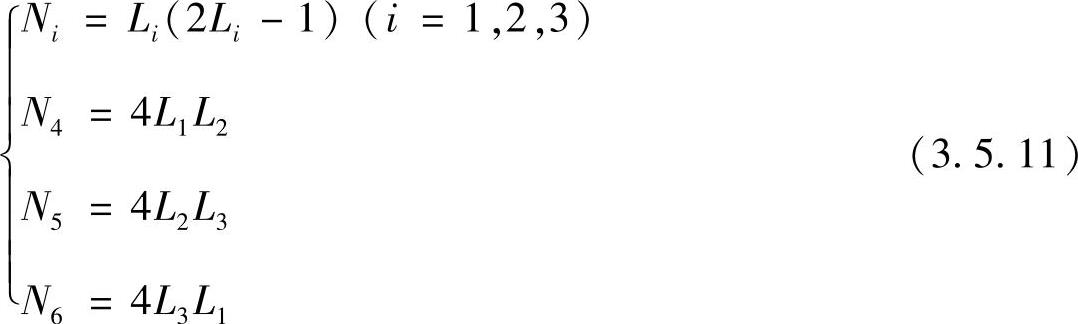
其中，L_i为三角形单元的面积坐标。

九节结三角形单元，其九个结点包括三角形的三个顶点和三条边的三分点。十结点是在九结点的基础上，再补加单元的形心，如图3.5.3所示。完整的三次多项式有10项，10个系数，三角形单元上设置10个结点。

在帕斯卡三角形中，取10项的完整三次多项式，其用面积坐标表示为

N_i=a_1i+a_2iL₁+a_3iL₂+a_4iL²₁+a_5iL²₂+a_6iL₁L₂+a_7iL²₁L₂+a_8iL1L₂²+a_9iL³₁+a_10iL₂³

只需将三角形单元中的如图3.5.2所示的6个结点的面积坐标值L_1，j，L_2，j，L_3，j（j=1，2，…，10），代入上式中，并按条件式

N_i（L_1，j，L_2，j，L_3，j）=δij（i，j=1，2，…，10）

即可建立10个含有a_1i，a_1i，…，a_10i的线性代数方程组。求出插值多项式的各组系数，插值函数为

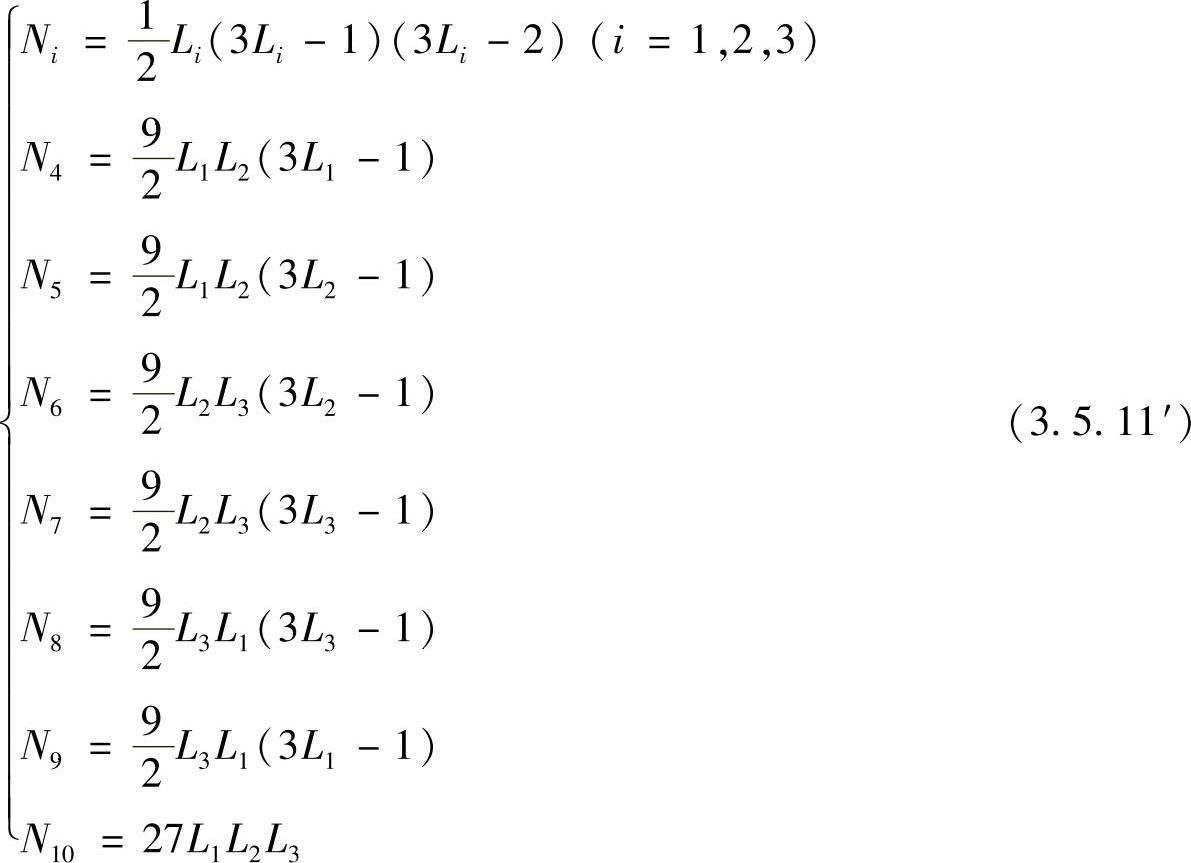(www.daowen.com)

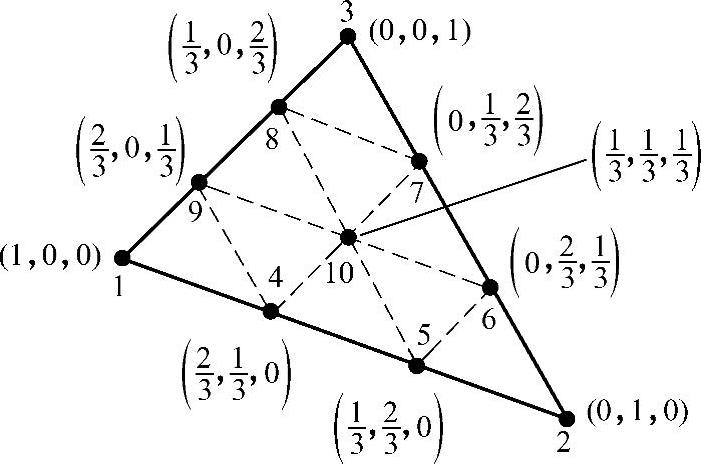
图3.5.3 九结点和十结点三角形单元

九结点三角形单元插值函数的构成并不是唯一的，下面给出的九结点三角形单元形函数相应的插值包含完全的二次多项式

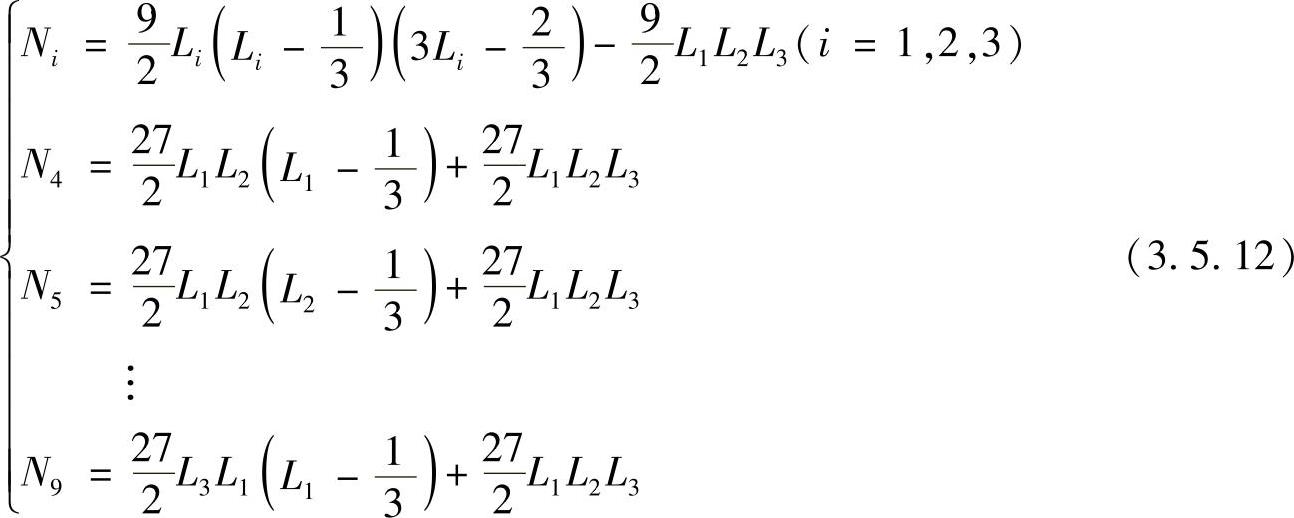
一般说来，若三角形单元中需采用更高次的插值多项式，则必须增加单元中的结点。N次完备的多项式有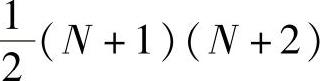项，因此三角形单元中应设置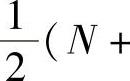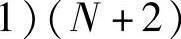个结点。图3.5.4和图3.5.5分别给出了四次和五次多项式的三角形单元的结点位置与序号。

对于高次插值多项式的各个系数，也可以仿照二次和三次的办法定出。当然，求解高阶线性代数方程组，是相当繁琐的，下面给出一种比较简便的确定各个插值多项式的方法。对于N次完备多项式结点共计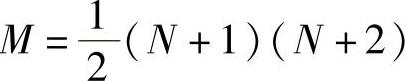个，相应于结点序号i的插值多项式为

N_i=B_i（L₁）B_i（L₂）B_i（L₃） （3.5.13）

其中，B_i（L_l）是如下定义的多项式

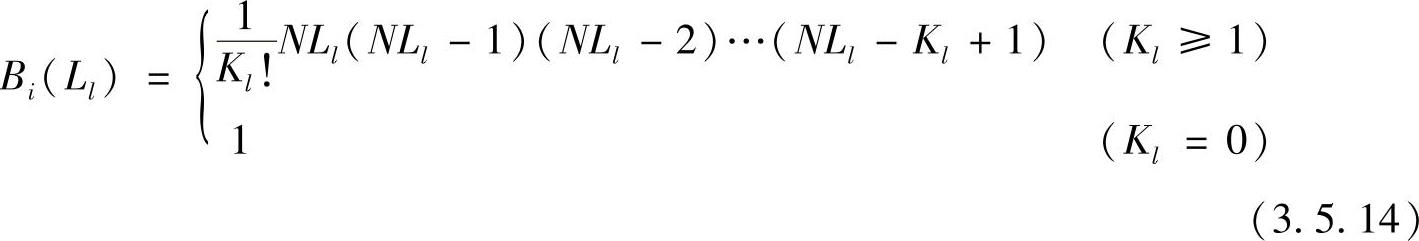
式中，K_l=NL_l^（i），L_l^（i）是面积坐标L_l在i号结点处的值（l=1，2，3；i=1，2，…，M）。若以三次插值多项式为例，按上述方法构造插值函数N₁，此时N=3，i=1，如图3.5.3所示，L₁^（1）=1，L₂^（1）=0，L₃^（1）=0，K₁=3，K₂=0，K₃=0，按式（3.5.14）有

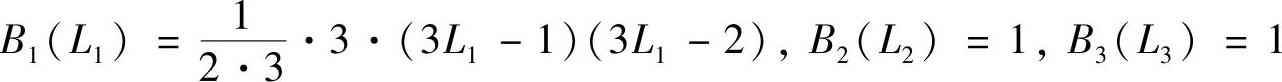
于是，根据式（3.5.13）有

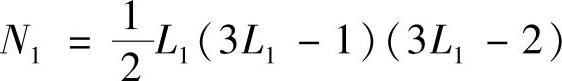
再看N₁₀，此时N=3，i=10，如图3.5.3所示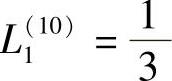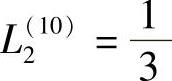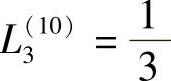，，，，K₁=1，K₂=1，K₃=1，按式（3.5.14）有

B₁（L₁）=3L₁，B₂（L₂）=3L₂，B₃（L₃）=3L₃

于是，根据式（3.5.13）有

N₁₀=27L₁L₂L₃

上述结果与前面采用的插值条件求解线性代数方程组所得出的结果完全一致。按照这个方法，可完全确定图3.5.4和图3.5.5所示的三角单元中，拉格朗日四次插值多项式和五次插值多项式的全部系数。

4.八结点与九结点以及十二结点四边形单元

若曲线四边形单元边线是二次曲线，那么可在单元中布置8个结点，除4个顶点外，每条边线上可以布置一个结点，边线的二次曲线形状完全由这条边线上的三个结点的位置决定。与它对应的基本单元是八结点正方形单元，只要将基本单元中的二次拉格朗日插值函数作为坐标变换关系式中的等参函数，就可以将二次曲线四边形单元和八结点正方形单元一一对应起来。

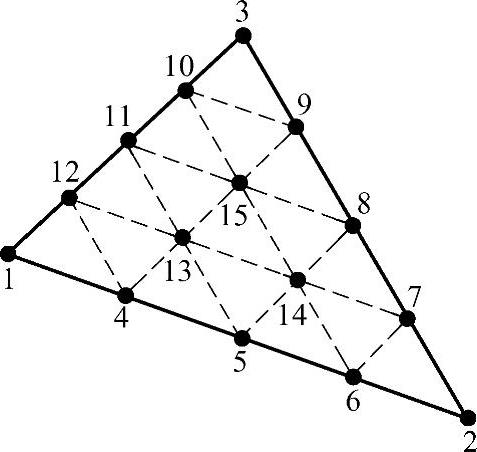
图3.5.4 六结点三角形单元

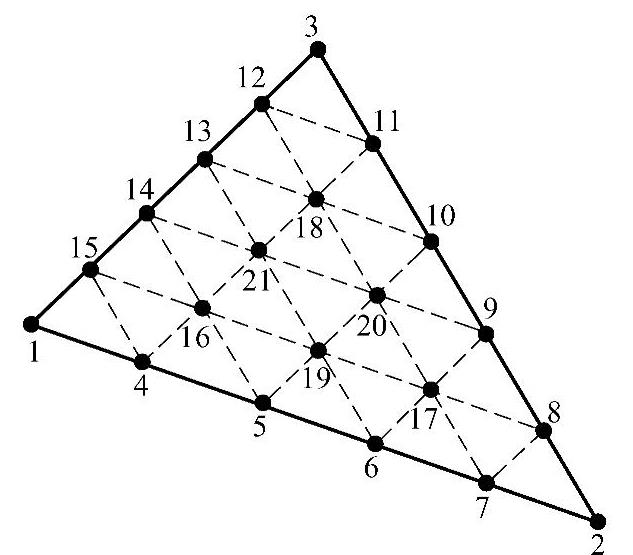
图3.5.5 九结点和十结点三角形单元

在八结点四边形单元的基础上，再加上单元的形心点则为九结点四边形单元，四边形单元的局部坐标为双向长度坐标（ξ，η），如图3.5.6所示。九结点四边形单元的形函数为

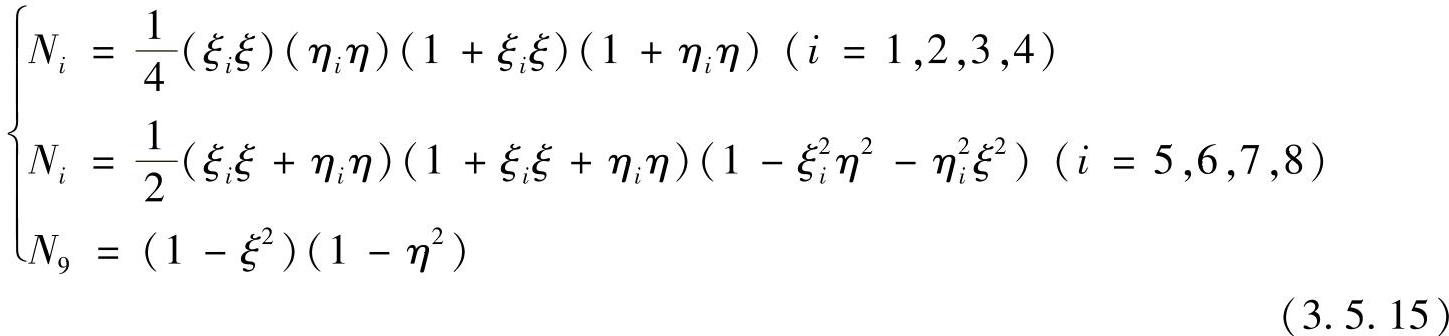
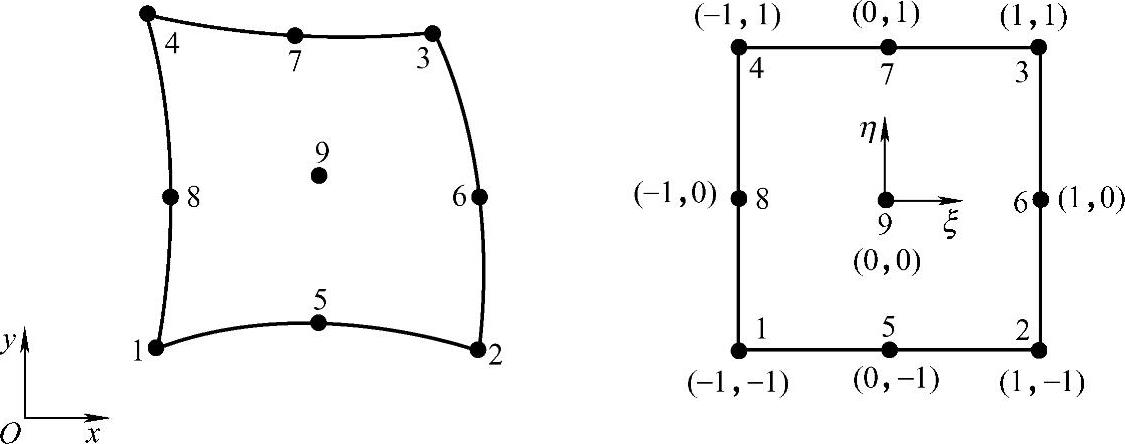
图3.5.6 八结点和九结点四边形单元

八结点四边形单元的形函数为

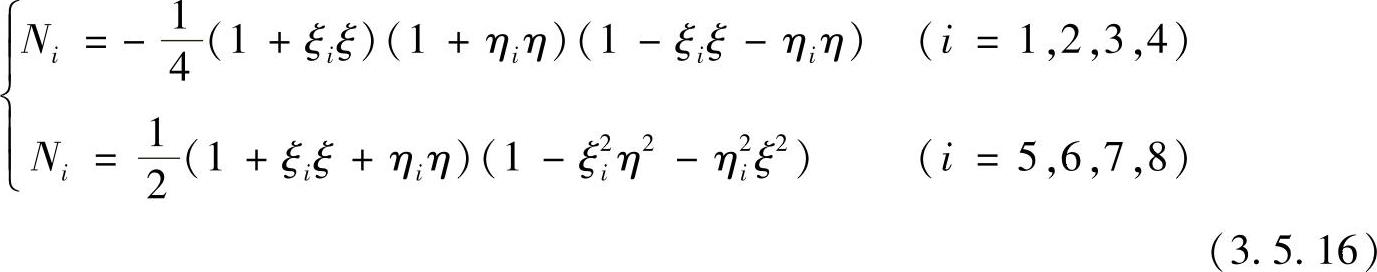
十二结点四边形单元如图3.5.7所示，这种单元的形函数为

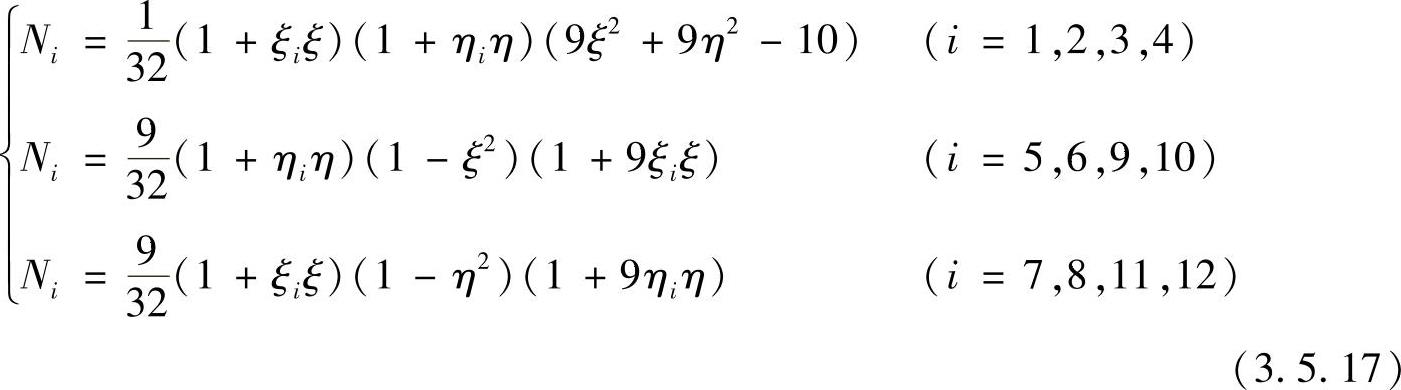
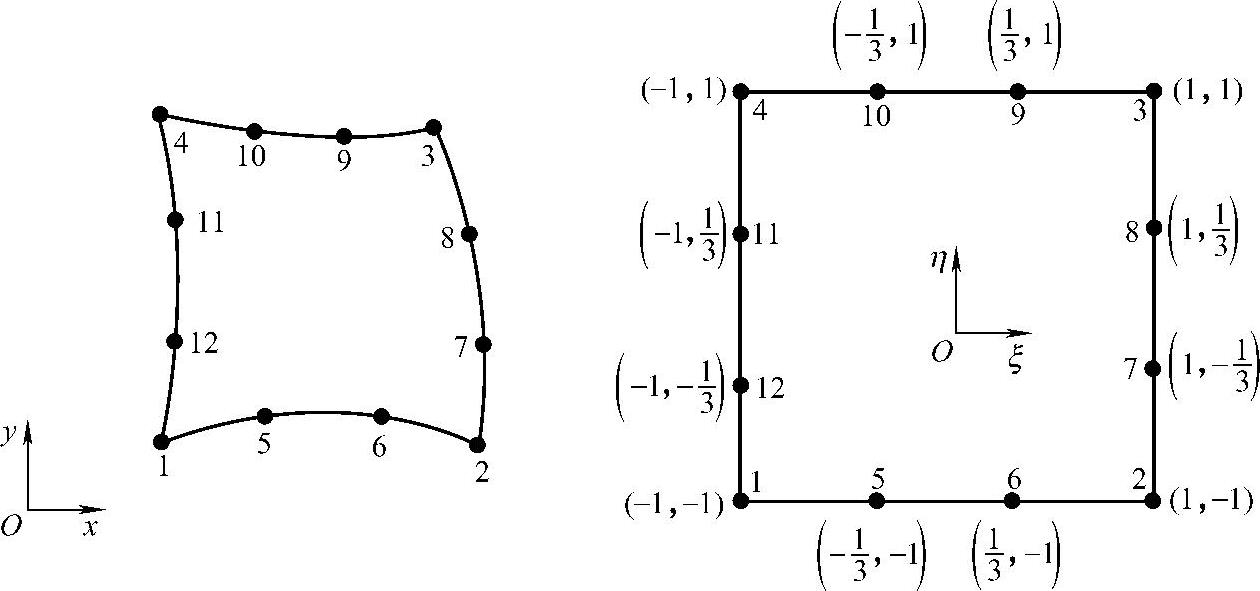
图3.5.7 十二结点四边形单元

5.十结点和二十结点四面体单元

十结点四面体单元如图3.5.8所示，它的10个结点包括4个顶点和6条棱边的中点，选用局部体积坐标，其形函数为

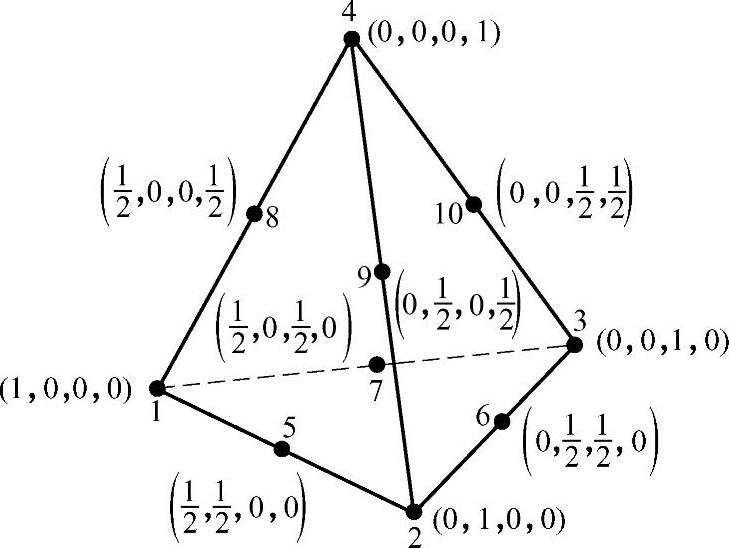
图3.5.8 十结点四面体单元

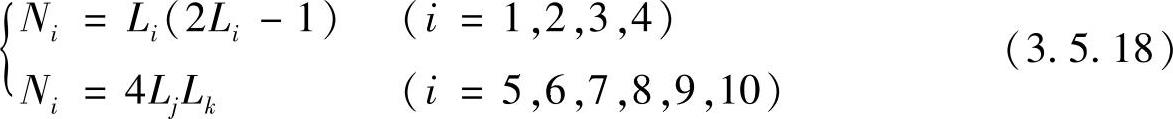
式中，j，k为结点i两侧的顶点编号。

二十结点四面体单元如图3.5.9所示，它的20个结点包括4个顶点，6条棱

边的12个三分点和4个边界面的形心。其形函数用体积坐标表示为

对于顶角结点

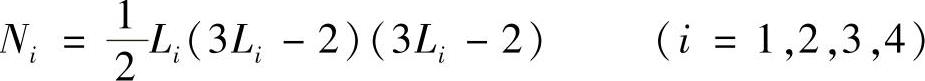
六条棱边上的结点

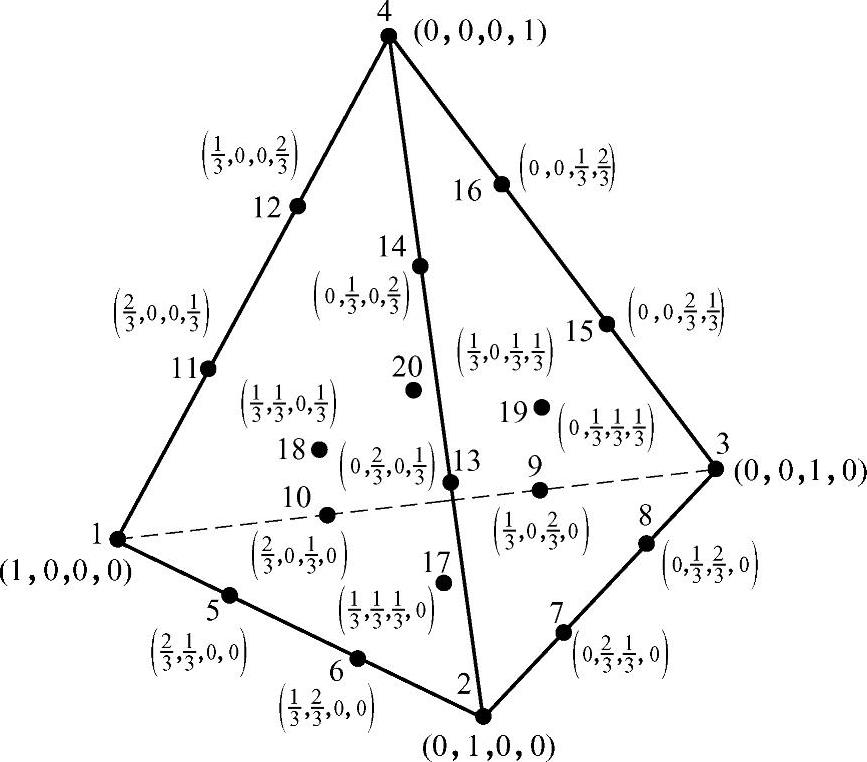
图3.5.9 二十结点四面体单元

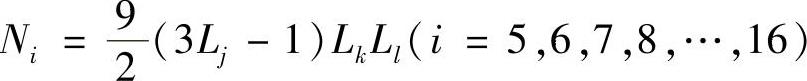
其中，j，k，l按结点i的顺序分别为j=1，2，2，3，3，1，1，4，2，4，3，4；k=1，2，2，3，3，1，1，4，2，4，3，4；l=2，1，3，2，1，3，4，1，4，2，4，3。

各个三角形侧面上形心处的结点

N_i=27L_jL_kL_l（i=17，18，19，20）

其中，j，k，l按结点i的顺序分别为j=1，2，3，4；k=2，3，4，1；l=3，4，1，2。

6.二十结点六面体单元

单元的20个结点包括8个顶点，12条棱边的中点，如图3.5.10所示，单元的形函数为

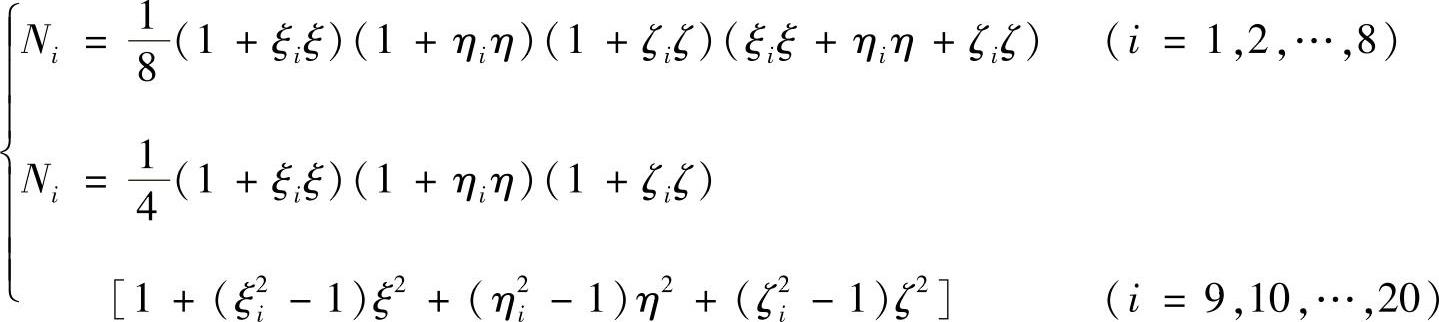
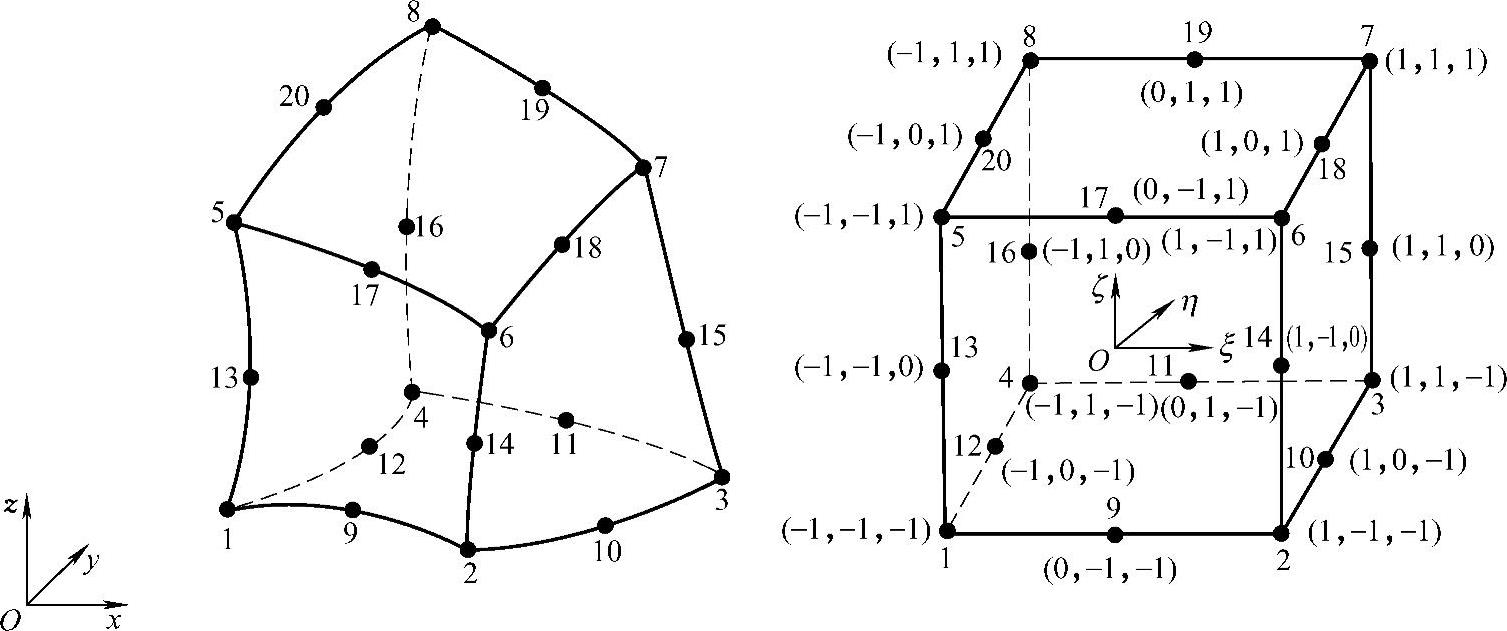
图3.5.10 十二结点六面体单元