1.基本单元及其应用特点
前已述及,基本单元是指边界平直的子区域,只取它的顶点为单元的结点,且只用结点的待定函数作为结点参数值,基本单元内的插值函数是拉格朗日多项式。基本单元的近似函数和坐标的各分量可以表示为

其中,i=1,2,…,r为单元的结点序号,r为单元的结点数。单元结点的整体坐标为(xi,yi,zi)(i=1,2,…,r),局部坐标为(ξi,ηi,ζi)(i=1,2,…,r),插值函数N可写为局部坐标的函数,也可变换为整体坐标的函数。
基本单元具有下面的应用特点:
1)基本单元的形态简洁,应用广泛,坐标变换和插值函数都是线性的,且具有相同的模式,基本单元在相邻公共边界上是相容的,保持函数是连续的。
2)基本单元在单元分析中,对整体坐标的微分和积分运算改用对局部坐标的运算,这需要用到坐标变换。基本单元的局部坐标是无因次的自然坐标,它与直角坐标之间的对应关系可用形函数表示出来。在局部坐标系中单元是规则的,形函数容易构成,故此法还可推广到其他类型的单元。
3)为了提高计算精度,三角形单元和四面体单元不应取得太尖太扁,四边形和六面体单元应取凸形的,且不应太尖太扁。
基本单元常用的单元形状有一维二结点直线段,二维三结点三角形和四结点四边形,三维四结点四面体和八结点六面体等。用在这类单元上的插值函数是线性、双线性或三线性的多项式,下面我们来讨论这些单元的插值函数。
2.二结点直线段单元
这种单元的拉格朗日插值多项式只有两项,取
Ni(x)=ai+bix(i=1,2) (3.4.8)
由插值条件式(3.4.3),有
ai+bixj=δij
单元两个结点的坐标为x1,x2,令上式中的i,j分别取1和2,可解得系数ai,bi,代回式(3.4.8),即得插值形函数

前面已经讨论过,有限元法的单元分析一般采取有普遍意义的无量纲局部坐标,如图3.4.2所示。若原点取在结点1上,作变换
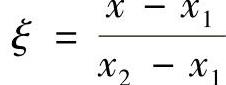
则插值函数式(3.4.9)可改写为

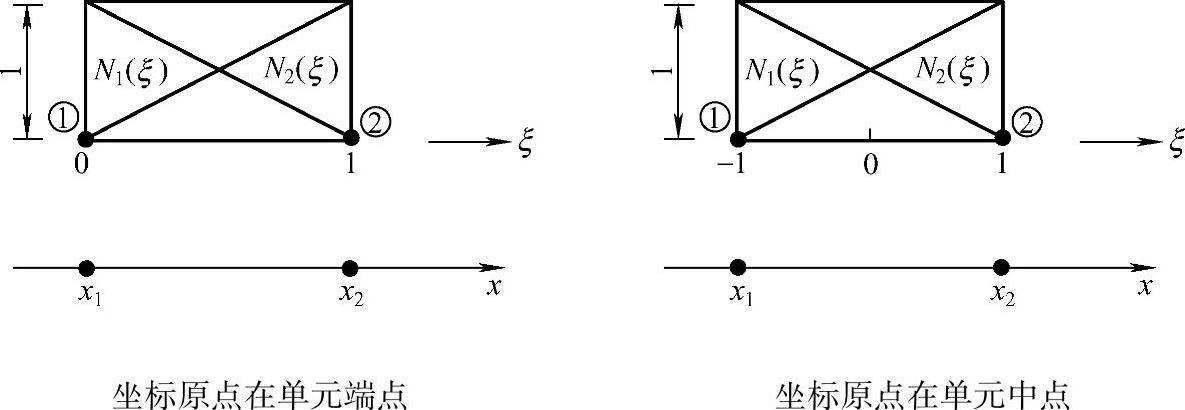
图3.4.2 一维两结点线性插值单元
若原点取在单元的中点,可作变换
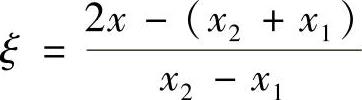
插值函数为
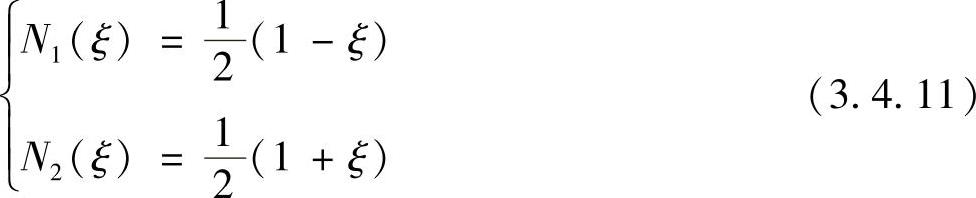 (https://www.daowen.com)
(https://www.daowen.com)
可以看到,插值函数式(3.4.9)和式(3.3.1)中的长度坐标相同,插值函数式(3.4.11)和式(3.3.7)中的长度坐标相同。实际上,可以直接取自然坐标为插值函数。有了插值函数,一维基本单元的近似函数根据式(3.4.6)可写为
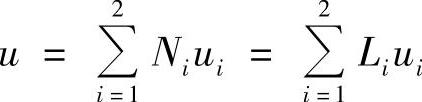
3.三结点直线段单元
这种单元的自由度为3,采用3个系数的拉格朗日线性插值多项式
Ni=ai+bix+ciy(i=1,2,3) (3.4.12)
应用插值条件式(3.4.2),可得
ai+bixj+ciyj=δij
其中,i,j分别取三角形单元的结点序号1,2,3,可求得系数ai,bi,ci,将这些系数代回式(3.4.12),便可得到插值函数,所得的插值函数完全与式(3.3.13)、(3.3.14)的自然坐标相同,这说明三结点三角形单元的插值函数Ni可直接取自式(3.3.14)中的面积坐标Li。根据式(3.4.6),单元的近似函数为
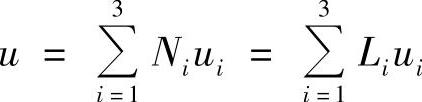
4.四结点四边形单元
四结点四边形单元具有四个自由度,如图3.3.8所示,可取插值函数为
Ni=ai+biξ+ciη+diξη(i=1,2,3,4) (3.4.13)
根据图3.3.8所示的结点序号和局部坐标,将式(3.4.13)在各结点上取值,并按插值条件,得
Ni(ξi,ηi)=δij(i,j=1,2,3,4)
可建立求解ai,bi,ci,di等系数的代数方程组,解出上述系数并代回式(3.4.13),即可得到插值函数,其结果与式(3.3.19)完全相同,这时单元的近似函数为
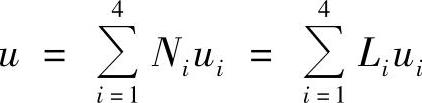
其中,Li按式(3.3.19)取值。
5.四结点四面体单元
四结点四面体单元的结点位置和序号如图3.3.10所示,相应的拉格朗日线性插值函数可取
Ni=Li(i=1,2,3,4)其中,自然坐标Li取式(3.3.24)的体积坐标。
6.八结点六面体单元
八结点六面体单元可以通过式(3.3.27)的变换关系式和自然坐标系中的正立方母单元进行变换,参见图3.3.12。单元的插值函数取式(3.3.28)中的自然坐标
Ni=Li(i=1,2,…,8)
单元中的近似函数为
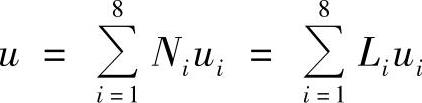
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






