1.单元的近似函数

单元中的近似函数通常都是以结点参数值和单元形函数的线性组合来表示的，可写为

u_i=α_iN_i （3.4.1）

其中，α_i为近似函数的广义坐标；N_i为单元的形函数，或称为基函数。

α_i表示单元中各结点的参数值，一般是结点待求的函数值以及函数的导数值，当形函数N_i选定之后，近似函数就完全由广义坐标α_i的值来确定。由于广义坐标α_i代表结点上的待求参量，于是要求形函数N_i应满足某种插值条件，故通常也称N_i为插值函数。

2.插值函数的构造条件

在有限元法中，当单元划分得越来越密时，则要求近似函数趋近于求解函数。由此，根据数学上的要求，构成近似函数的插值函数应能保证单元之间求解函数及其导数的连续性，即在连续性上必须满足协调条件和完备条件。协调条件也称为相容条件，即要求相邻单元的近似函数或其导数在单元交接边界上是连续的。完备条件是指当单元缩小到一点时，有限元积分表达式中函数的各阶导数都应趋于某一确定值，即要求单元中近似函数的各阶导数不间断。由于近似函数的导数阶次比积分表达式中函数导数低一阶，因此要求近似函数在单元内部与积分表达式中函数的导数同阶，在单元交接边界上可低一阶。

在近似解的基函数展开式中，基函数应选自完备的线性无关序列。一般而言基函数采用不同幂次的单项式，而近似函数则是完整的多项式形式，即应该完整地包括零次幂项（常数项）及由低到高的各个幂次项，其最高的幂次决定了单元插值函数的阶次。这样依照完备序列的定义，当基函数的个数无限增加时，构造的近似解能够充分逼近满足相同容许条件的任意函数。只要适当地选择系数，近似解就可以逼近准确解。另一方面，当单元缩小到一点时，泛函积分表达式中函数的各阶导数都应趋于一个确定的常数，使单元中近似函数的各阶导数不间断。

3.插值函数的类型

在有限元法中，通常插值函数都采用多项式，因多项式便于微分和积分运算。如前文所述，用作插值函数的多项式有两大类，其中一类只要求插值多项式在插值结点上取已知值，即拉格朗日型插值多项式；另一类是要求插值多项式及其导数，包括若干阶导数或法向导数在插值结点上取已知值，即埃尔米特型插值多项式。拉格朗日插值多项式满足插值条件

N_i（x_j）=δ_ij（i，j=1，2，…，r） （3.4.2）

式中，N_i是单元中结点i所对应的插值函数；x_j为j结点的坐标；r为单元结点数。

将拉格朗日插值多项式作为单元基函数，每个结点对应一个基函数，如将单元中的近似函数式（3.4.2）在各结点上取值，即得广义坐标

α_i=u（x_i）（i=1，2，…，r）

于是近似函数的广义坐标就是结点的函数值u_i=u（x_i），则近似函数的表达式为

u=u_iN_i （3.4.3）

应用拉格朗日插值多项式作为基函数，只能保证单元结点上有确定值，使近似函数在单元边界上的连续性，而不能保证其导数的连续性。如要保证导数的连续性，一般要采用埃尔米特插值多项式。在有限元分析中，埃尔米特插值多项式所满足的插值条件为

其中，H_ki为单元中第i个结点所对应的第k阶埃尔米特插值多项式；x_j为第个j结点的坐标；结点序号指标i，j=1，2，…，I；I为单元内部结点总数；函数导数阶次指标l，k=1，2，…，K；K是作为结点参数的函数导数的最高阶次。

应用埃尔米特插值多项式（3.4.4），作为单元的基函数，对应结点i的基函数为H_0i，H_1i，…，Hki共k+1个基函数，近似函数式（3.4.3）成为(www.daowen.com)

u=u_iH_0i+u′_iH_1i+…+u_i（K）H_Ki （3.4.5）

式中，u_i（k）表示第i个结点的k阶导数值，即

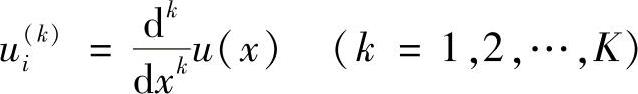
这时，代表结点参数的广义坐标α_i表示结点上的函数值和导数值。

4.单元的自由度与插值多项式的阶次和项数

在有限元分析中，根据求解问题的特性和精度要求，要合理选择单元中结点的参数类型与数目。参数类型是指求解时在结点上取什么样的参数，它反映了求解函数在结点上的特性。通常都将求解问题的函数值及其导数值取作结点参数，一个结点上的参数个数称为这个结点的自由度，单元中所有结点的参数个数称为单元的自由度。例如，对于一维二结点单元，若结点参数为函数值，则结点自由度为1，单元自由度为2，单元自由度和近似函数中的广义坐标个数是相等的，此时近似函数表达式为

u=u₁N₁+u₂N₂

若结点参数除函数值外，还有一阶、二阶导数值，则结点自由度为3，单元的自由度为6，此时近似函数表达式为

u=u₁H₀₁+u₂H₀₂+u′₁H₁₁+u′₂H₁₂+u″₁H₂₁+u″₂H₂₂

同理，对于三角形三结点单元，当结点参数为函数值时，单元的自由度为3。对于三角形六结点单元，当结点参数为函数值时，单元的自由度为6。

单元中插值多项式的项数应当和单元自由度数相等。例如，在三结点三角形单元中采用拉格朗日插值多项式，单元的自由度是3，多项式的项数也应为3，插值函数可写为

N_i=a_i+b_ix+c_iy

对于六结点的三角形单元，自由度为6，插值函数为6个系数的二项多项式

N_i=a_1i+a_2ix+a_3iy+a_4ix²+a_5ixy+a_6iy²

单元中插值多项式的阶次和项数除取决于单元的自由度之外，还应考虑到多项式的完整性和对称性。多项式的完整性是指多项式应完整地包括各个幂次项。当多项式的项数由单元的自由度确定之后，可以由多项式的完整性确定多项式的阶次。反过来，多项式的完整性决定了多项式应有一定的项数，即对于二维的情形，多项式的完整性可按帕斯卡（Pascal）三角形确定其阶次和项数，如图3.4.1所示，完整的多项式具有对于自变量x，y的对称性。

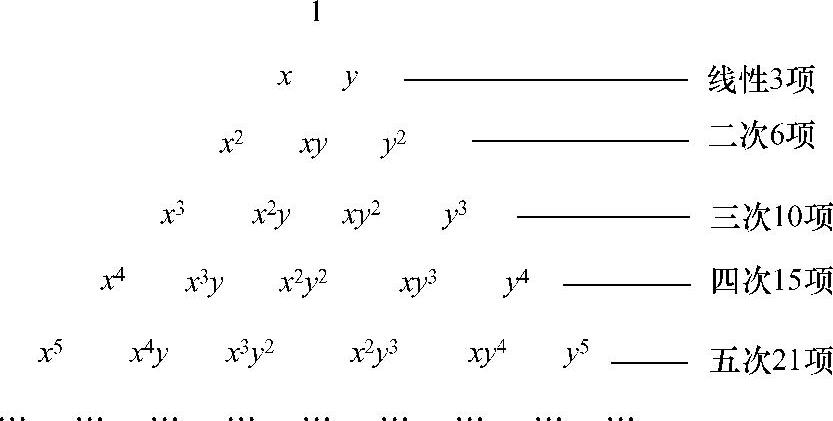
图3.4.1 帕斯卡三角形（杨辉三角形或贾宪三角形）

通常，可按完整多项式的项数在单元中设置结点，有时可减少一些内部结点以简化计算，相应要减少多项式的一些项数，这时要保持多项式的对称性。多项式的完整性和对称性可以保证插值多项式在几何上的各向同性，以便在坐标系作转换时不影响插值多项式的表达形式，保证近似函数在不同的坐标系中有相同的解。