我们知道，在许多实际问题中，函数y=f（x）在某区间[a，b]上存在，但函数关系往往很复杂，甚至没有明显的解析表达式，例如，通过实验或观测得到一系列数据，这些数据是与自变量的某些点x_i相应的函数值y_i，而我们需计算未观测到的点的函数值。根据已观测数据来构造一个既能反映函数的特征又便于计算的而且较为简单的函数p（x）来替代f（x），此即插值问题。

设函数y=f（x）定义在区间[a，b]上，x₀，x₁，…，x_n是[a，b]上的n+1个互异点，且仅仅在这些点处函数值y_i=f（x_i）为已知，要构造一个函数p（x），使得

p（x_i）=y_i（i=0，1，…，n）

并要求误差

R（x）=f（x）-p（x）

的绝对值|R（x）|在区间[a，b]上任意一点或整个区间[a，b]上比较小，即说明p（x）较好地逼近了f（x）。点x₀，x₁，…，x_n称为插值基点或简称为基点。p（x）称为插值函数，f（x）为被插函数，求f（x）的插值函数的方法称为插值法，R（x）称为插值公式的余项。插值函数p（x）在n+1个插值基点x_i（i=0，1，…，n）处的值与f（x）相等，在其他点就用p（x）的值作为f（x）的近似值。

我们用p（x）作为f（x）的插值函数，除要求p（x）在某些意义上更好地逼近f（x）外，还希望f（x）是较简单的函数，或者它便于计算机计算，因此，我们常用多项式、有理分式和三角多项式作为插值函数。选择不同的函数类作为插值函数逼近f（x），其效果是不同的，需根据实际问题中被插函数f（x）的特性，来选择合适的插值函数，例如，可选取多项式作为插值函数，此即所谓的插值多项式。若p（x）是次数不超过n的多项式，用P_n（x）表示，即

P_n（x）=α₀+α₁x+α₂x²+…+α_nxⁿ

则称P_n（x）为n次插值多项式。可以证明，在所有次数不超过n的多项式中，满足插值函数要求的P_n（x）存在且唯一。

我们考虑最简单的插值问题，设函数在区间[a，b]上n+1个互异基点x₀，x₁，…，x_n上的函数值为

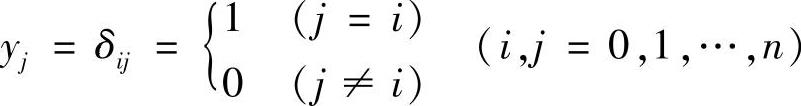
求插值多项式l_i（x），满足条件

l_i（x_j）=δ_ij（i，j=0，1，…，n）

由上式知，x₀，x₁，…，x_i-1，x_i+1，…，xn是li（x）的根，于是可令

l_i（x）=A_i（x-x₀）（x-x₁）…（x-x_i-1）（x-x_i+1）…（x-x_n）

再由l_i（x_i）=1，得

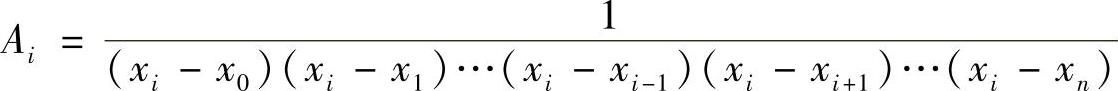
于是

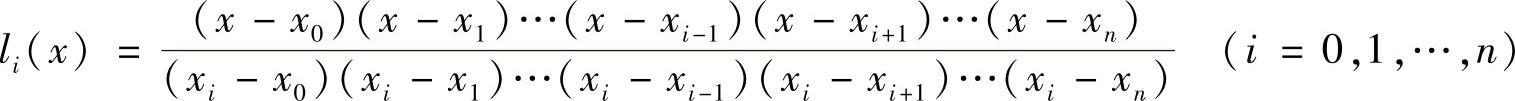
这样就得到n+1个n次多项式l₀（x），l₁（x），…，l_n（x），称为插值基函数。

当n=1时的一次基函数为

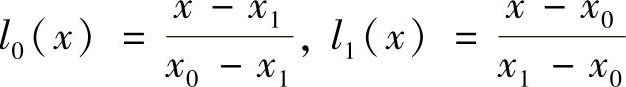
当n=2时的二次基函数为

一般地，设函数在区间[a，b]上n+1个互异基点x₀，x₁，…，x_n上的函数值分别为y₀，y₁，…，y_n，若n次插值多项式I_n（x），满足条件

L_n（x_j）=y_j（j=0，1，…，n）

则有拉格朗日插值多项式

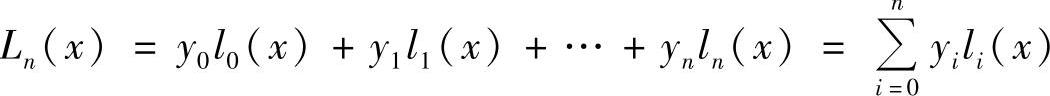
其中，l₀（x），l₁（x），…，l_n（x）为n次插值基函数。

拉格朗日插值多项式的插值条件只要求在插值基点上插值函数与被插值函数的函数值相等，即L_n（x_i）=y_i，有时不仅要求插值多项式在插值基点上与被插值函数的函数值相等，还要求插值多项式的导数在这些点上与被插函数的导数值相等，即要求满足插值条件

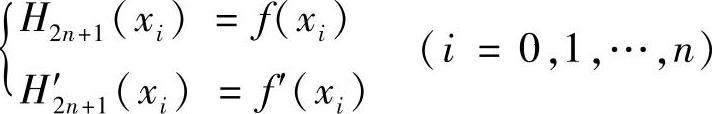
的次数不超过2n+1的插值多项式H_2n+1（x），这就是埃尔米特（Hermite）插值。下面对埃尔米特插值作简要讨论。

设在结点a≤x₀＜x₁＜…＜x_n≤b上，y_j=f（x_j），m_j=f′（x_j）（j=0，1，…，n）

要求插值多项式H（x）满足条件

这里给出了2n+2个条件，可唯一确定一个次数不超过2n+1的多项式

H_2n+1（x）=H（x）

其形式为

H_2n+1（x）=a₀+a₁x+…+a_2n+1x²ⁿ⁺¹

显然，直接根据H（x）满足的条件确定2n+2个系数a₀，a₁，…，a_2n+1将非常复杂，为此，我们仍采用拉格朗日插值多项式的基函数方法，先求插值基函数α_j（x）和β_j（x）（j=0，1，…，n），共有2n+2个，每一个基函数都是2n+1次多项式，且满足条件

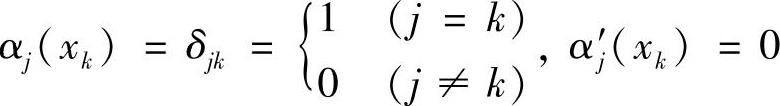(www.daowen.com)

β_j（x_k）=0，β_j′（x_k）=δ_jk（j，k=0，1，…，n）

于是，插值多项式H（x）=H_2n+1（x）写成用插值基函数表示的形式

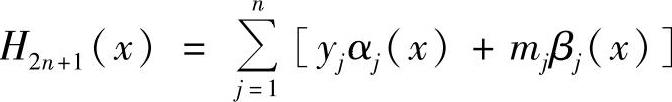
根据限定条件，显然有

H_2n+1（xk）=y_k，H₂′_n+1（xk）=mk（k=0，1，…，n）现在的问题就是求满足条件的基函数α_j（x）和β_j（x），为此，可利用拉格朗日插值函数l_j（x）。

下面我们考虑只有两个结点的三次埃尔米特插值。设插值点为（x₀，y₀），（x₁，y₁），要求次数不超过3的多项式H₃（x），满足下列条件

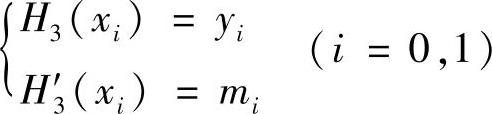
式中，m_i=f′（x_i）（i=0，1）。

类似于拉格朗日插值多项式的构造过程，仍采用基函数的方法来构造H₃（x），令

H₃（x）=y₀α₀（x）+y₁α₁（x）+m₀β₀（x）+m₁β₁（x）

式中，α₀（x），α₁（x），β₀（x），β₁（x）是插值基函数，为了满足插值条件，它们应满足下列条件（见表3.4.1），且α₀（x），α₁（x），β₀（x），β₁（x）均为次数不超过3的多项式。

表3.4.1 插值基函数

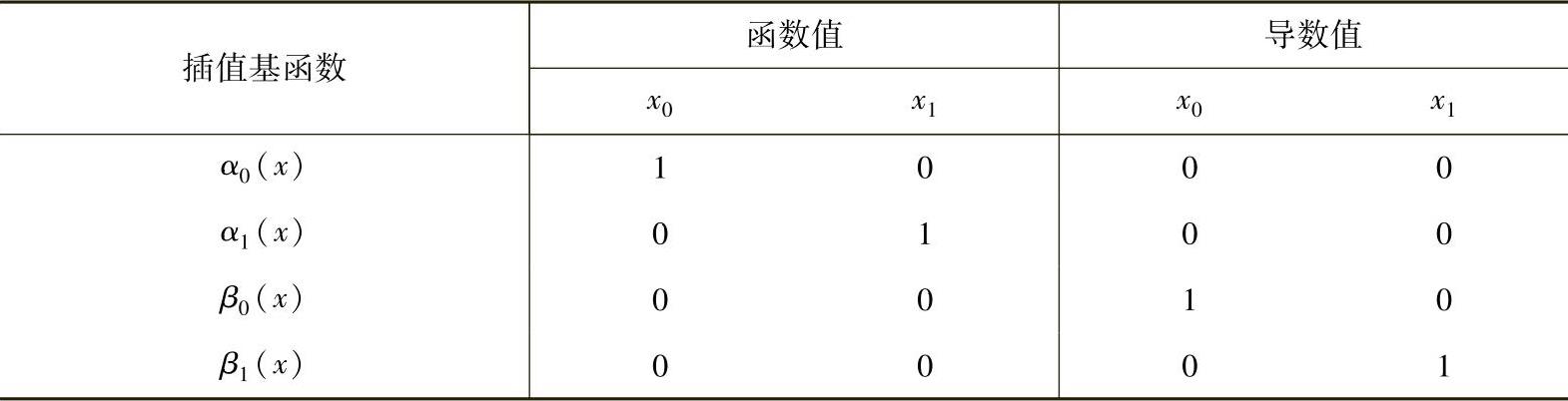
由表3.4.1可知，α₀（x₁）=α₀′（x₁）=0，故α₀（x）应含有（x-x₁）2因子，又α₀（x）是次数不过3的多项式，因而可将它写成

α₀（x）=[a+b（x-x₀）]（x-x₁）2式中，a，b为待定常数。由α₀（x₀）=0，得

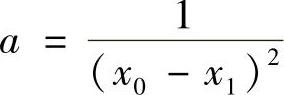
由α′₀（x₀）=0，得

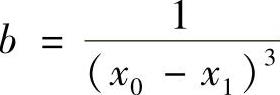
于是

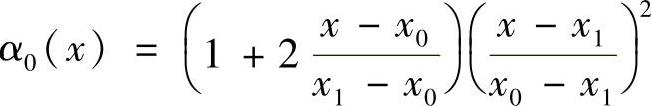
类似地，可得到α₁（x）为

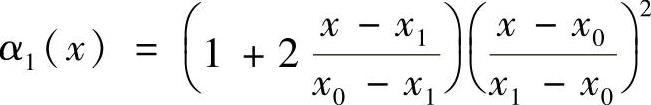
对于β₀（x），注意到β₀（x₀）=β₀（x₁）=β₀′（x₁）=0，于是β₀（x）应含有（x-x₀）（x-x₁）2因子，又β₀（x）是次数不过3的多项式，因而可将它写成

β₀（x）=c（x-x₀）（x-x₁）2

式中，c为待定常数。

由β₀′（x₀）=1，得

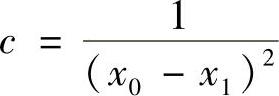
于是

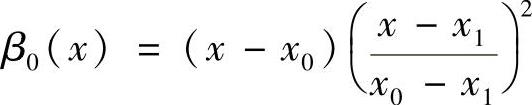
类似地，得到

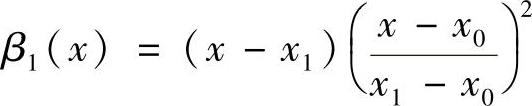
显然α₀（x），α₁（x），β₀（x），β₁（x）可简单地表示为

α₀（x）=[1+2l₁（x）]l²₀（x）

α₁（x）=[1+2l₀（x）]l²₁（x）

β₀（x）=（x-x₀）l₀²（x）

β₁（x）=（x-x₁）l²₁（x）

其中，l₀（x），l₁（x）为以（x₀，y₀），（x₀，y₀）为插值点的拉格朗日一次基函数。

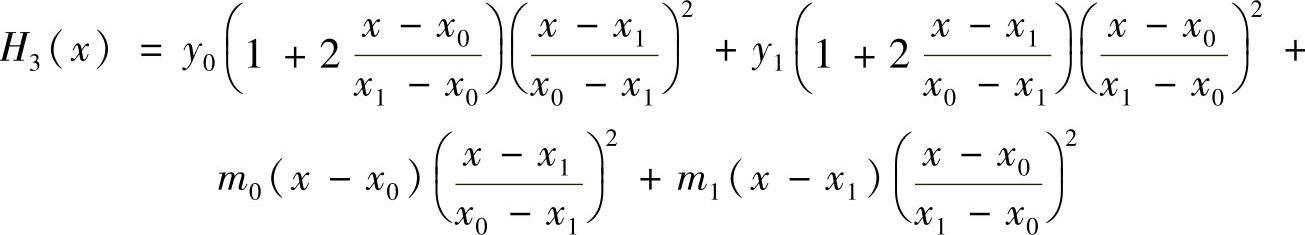
与拉格朗日插值类似，可以证明，三次埃尔米特插值多项式存在且唯一。