自然坐标：三角形子单元与母单元的联系方法

自然坐标系是一种无因次的局部坐标系，它根据单元在整体直角坐标系所定义的几何形状沿边界的主外结点之间从0到1取值。自然坐标系的性质是，若其中一个坐标在单元的某一外结点上的值为1，则在其余的外结点上的值为零，且在外结点之间的变化是线性的。可对二结点线段单元，三结点三角形单元，四结点四边形单元，四结点四面体单元和八结点六面体单元构造自然坐标系。这些单元和边界是直的，后面我们讨论等参单元时将会看到，自然坐标系还可用于曲边单元。

采用自然坐标系的目的是将称为子单元的同一类形状但大小不一的单元通过线性变换与对应的称为母单元的标准单元联系起来。对于自然坐标或对母单元，因其采用局部相对坐标，在求取单元的插值函数时特别方便，容易写出统一形式的形函数，便于单元分析中的微分和积分运算。

自然坐标系用单元的外结点坐标来描述单元内任意点的位置，一个坐标与某一外结点相联系，并在该点取值为1，通常用L_i（i=1，2，…，r）表示自然坐标，其中，r为单元的外结点数，自然坐标在一维、二维和三维的不同单元中分别取长度坐标、面积坐标或双向长度坐标、体积坐标或三向长度坐标。下面分别讨论不同单元采用的自然坐标和对应的母单元。

1.长度坐标

一维线段单元内的自然坐标采用的是长度坐标，如图3.3.4所示，考虑外结点为1和2的线段单元，沿线段取整体坐标x，单元的长度坐标L₁，L₂定义为

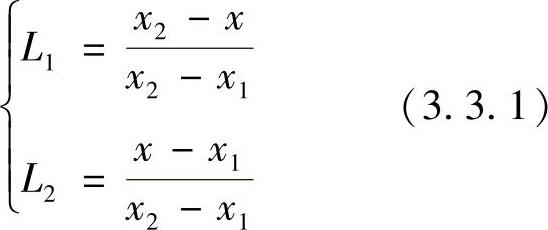
显然，单元两个外结点的长度坐标（L₁，L₂）分别为（1，0）和（0，1），且有

L₁+L₂=1 （3.3.2）

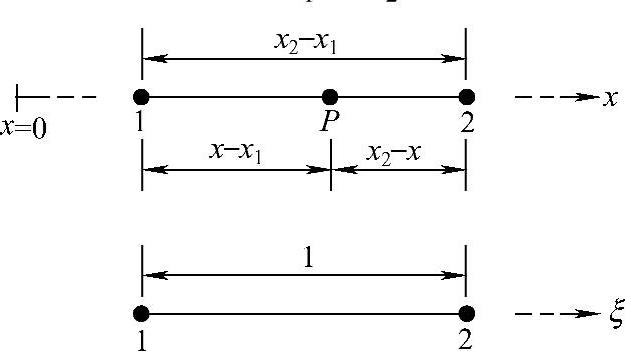
图3.3.4 一维线段单元长度坐标（1）

即两个自然坐标中只有一个是独立的。单元中某点P的自然坐标L₁，L₂和整体坐标x之间的关系可写成

x=L₁x₁+L₂x₂ （3.3.3）

式（3.3.2）和式（3.3.3）可统一写成

若取相对坐标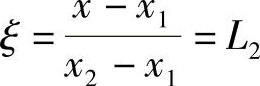，则长度坐标式（3.3.1）可写为

由式（3.3.1）、式（3.3.3）和式（3.3.5）可以看出，长度坐标（L₁，L₂）和整体坐标x之间的线性变换关系，通过上述变换可将任意长度的直线段或曲线段单元变换为长度等于1的直线段母单元。

对一维的自然坐标系，还可取长度等于2的直线段母单元，如图3.3.5所示，相对坐标原点取在母单元的中心，单元两个端点的局部坐标分别为ξ=-1和ξ=1，这时整体坐标和局部坐标的变换关系为

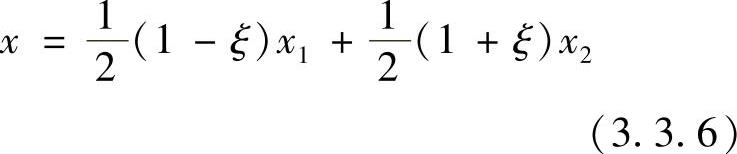
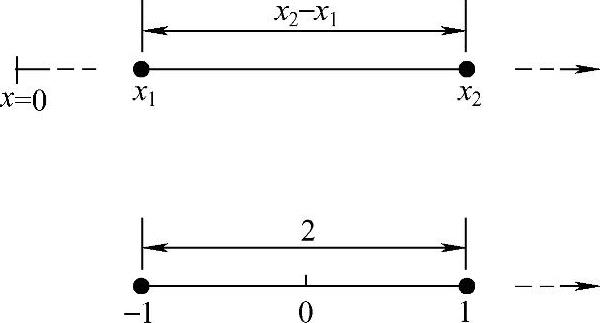
图3.3.5 一维线段单元长度坐标（2）

即单元的长度坐标为

式（3.3.7）中的自然坐标L₁，L₂在0～1内取值。

将求解函数转换为长度坐标L₁，L₂的函数后，对x的导数可根据复合函数的求导公式

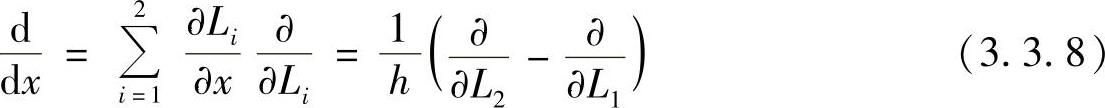
式中，h=x₂-x₁，为线段单元的长度。

长度坐标对于单元的积分经常使用，其公式计算为

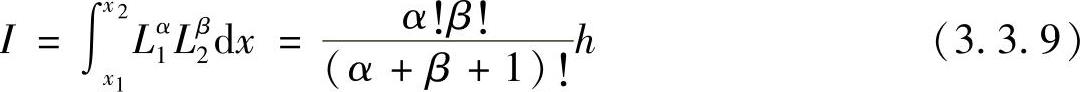
其中，α，β为整数幂。以下给出推导过程，事实上，利用分部积分公式，有

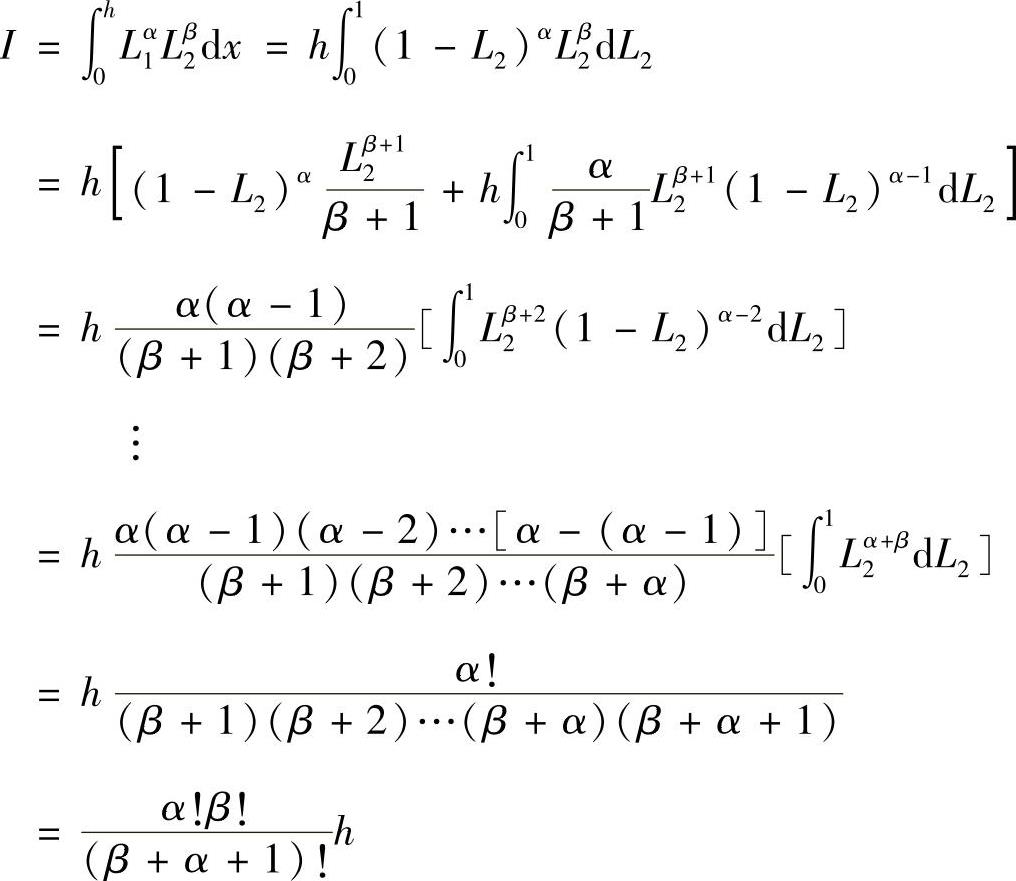
表3.3.1中列出了α，β取不同值时，式（3.3.9）的积分值。

2.面积坐标

二维三角形单元采用的面积坐标，定义三角单元的面积坐标L_i为

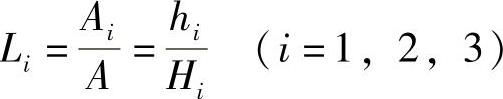
式中，A为三角形的面积；A_i为点P和结点i的对边所构成的三角形面积。例如，A₃等于△P12的面积，h_i为点P到结点i对边的距离，H_i为结点i到结点i对边的距离，如图3.3.6所示。

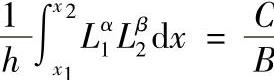
表3.3.1 长度坐标的积分

显然，三角形三个顶点的面积坐标分别为（1，0，0），（0，1，0），（0，0，1）。因A=A₁+A₂+A₃，故有

L₁+L₂+L₃=1 （3.3.10）

这说明三个自然坐标中只有两个是独立的，实际运算时，为了方便，三个坐标变量L₁，L₂，L₃经常同时使用。自然坐标系和直角坐标系的关系为

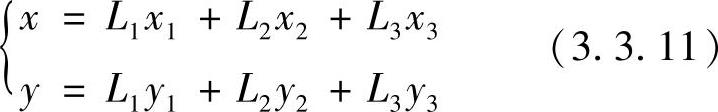
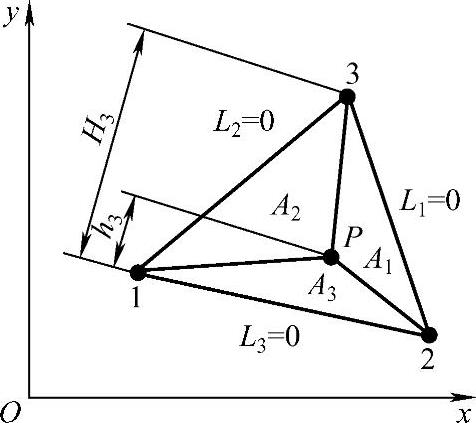
图3.3.6 三角形单元面积坐标

式（3.3.10）与式（3.3.11）可合写成矩阵的形式为

其中，x_i，y_i（i=1，2，3）分别为三角形单元三个顶点的直角坐标。由式（3.3.12）可求出用直角坐标表示的自然坐标

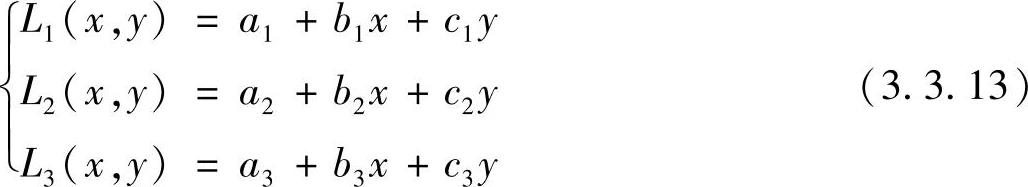
其中，

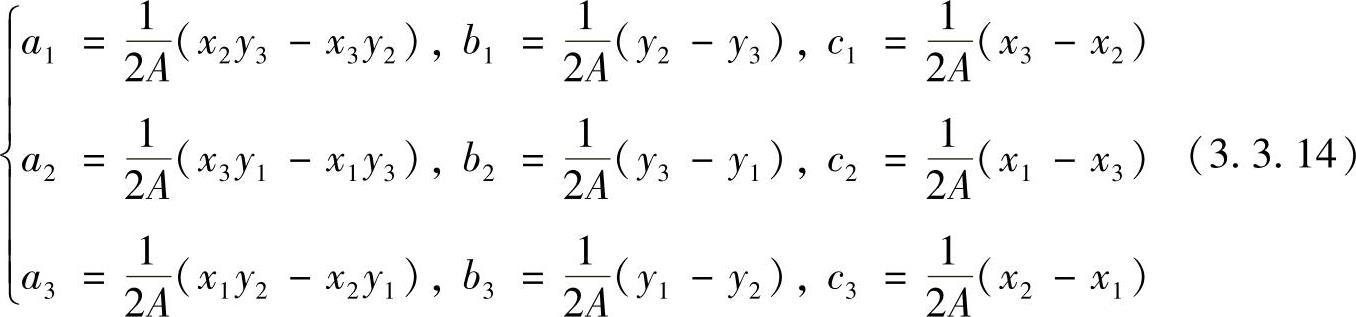
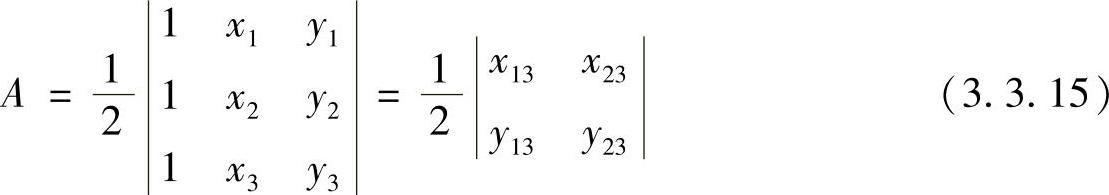
式中，A为三角形面积；x_ij=x_i-x_j；y_ij=y_i-y_j。

由式（3.3.11）和式（3.3.12）可知，面积坐标（L₁，L₂，L₃）与直角坐标（x，y）可通过线性变换将（x，y）平面上任意三角形单元变换到（L₁，L₂）平面上直角边为1的直角三角形单元，如图3.3.7所示。

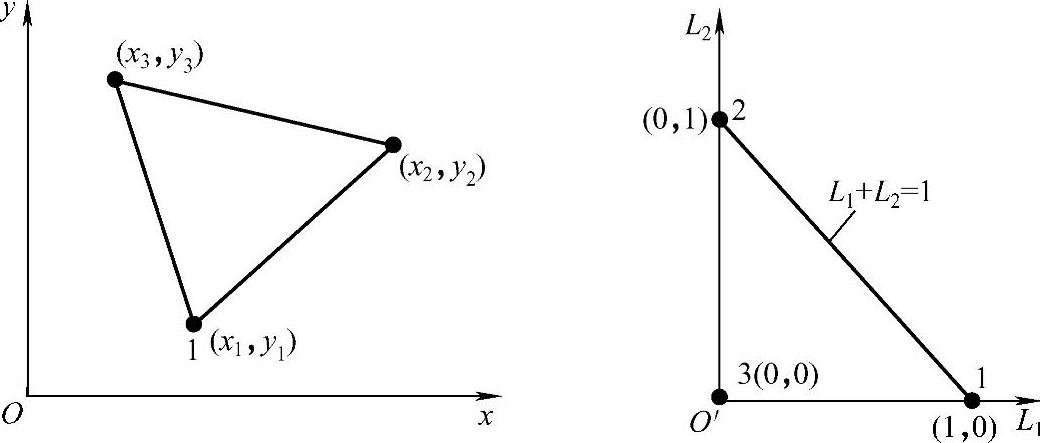
图3.3.7 任意三角形单元变换为直角三角形单元

由式（3.3.13）可以推导出下面的求导数公式

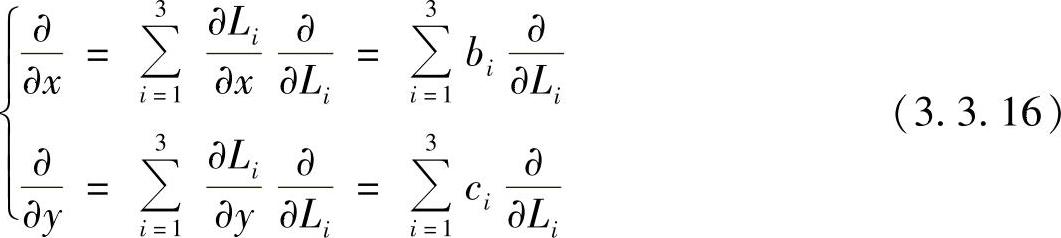
后面我们会看到，单元分析中的积分，由于基函数通常采用多项式函数，被积函数一般都是以幂函数形式出现的，因此在单元分析中经常涉及计算如下典型形式的积分，即

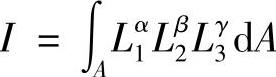
积分区域是三角形单元，其面积为A，其中，α，β，γ是任意自然数，积分结果是

积分公式（3.3.17）是采用三角形单元进行有限元分析时经常用到的，以下给出该公式的证明。

积分公式（3.3.17）中的面积微元

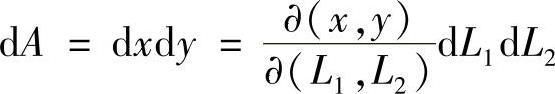
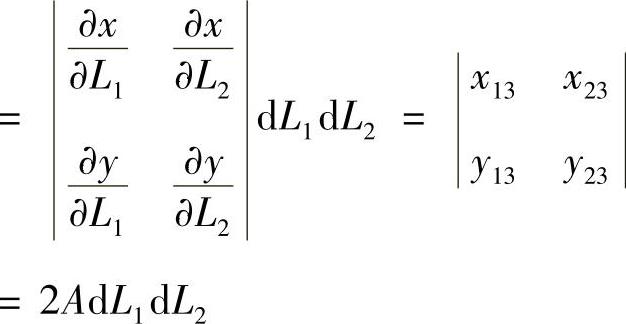
式中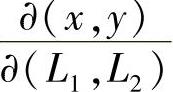，为坐标变换过程中的雅可比（Jacobi）行列式。参见图3.3.6，可以

得到

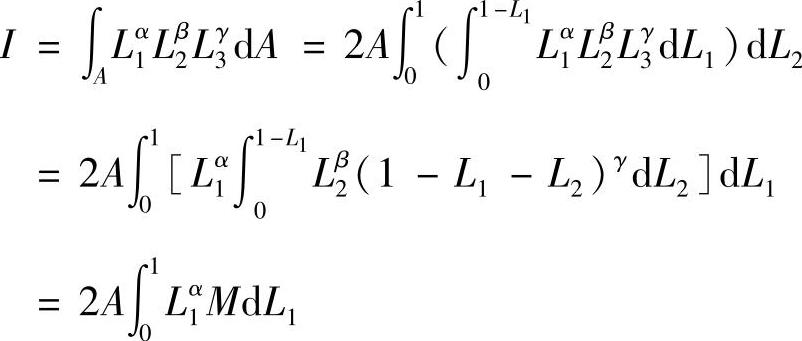
其中，

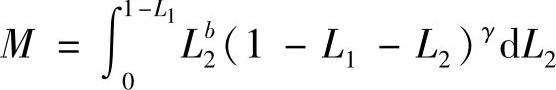
作变量代换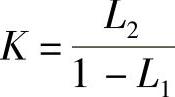，可得

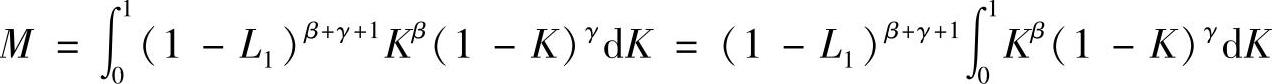
接下来的推导过程与式（3.3.9）的长度坐标对于单元的积分计算一致，即

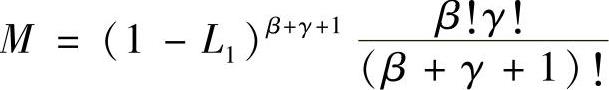
于是

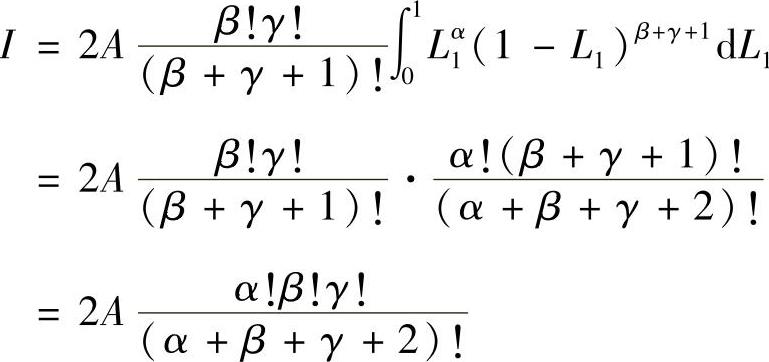
对于三维问题与此相仿，并可得出相似的结果显示。表3.3.2中列出了不同α，β，γ值时，式（3.3.17）的积分值。

3.双向长度坐标(https://www.daowen.com)

对于二维四边形单元，可建立如图3.3.8所示的自然坐标系，图中给出了整体直角坐标系内和局部自然坐标系内的四边形单元。

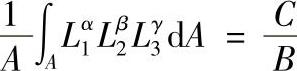
表3.3.2 面积坐标的积分

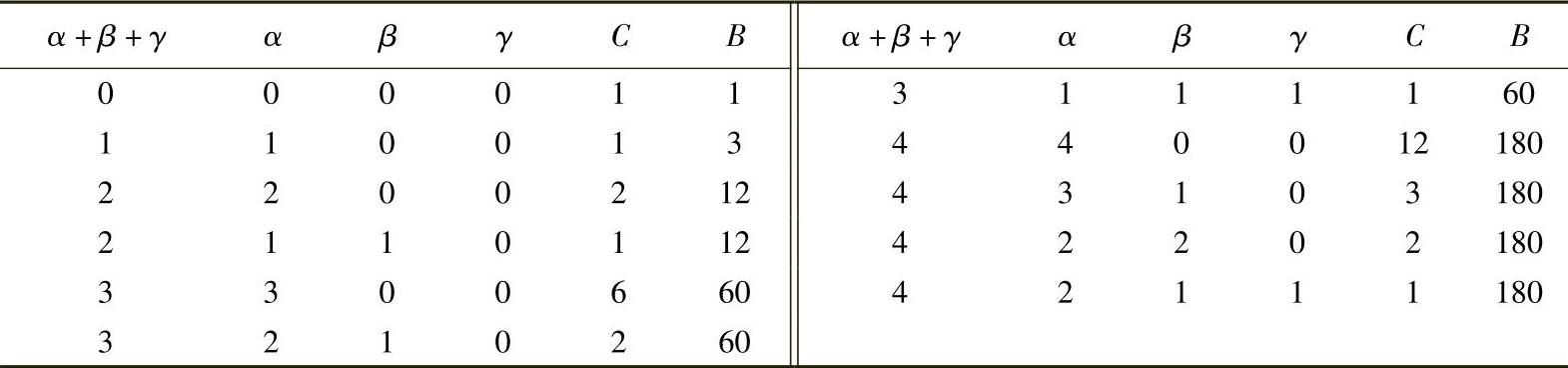
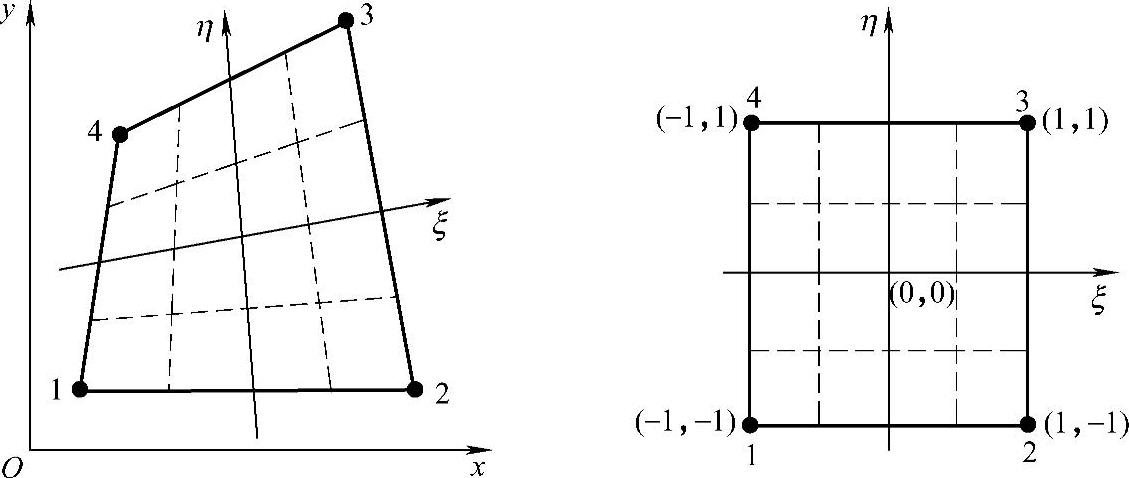
图3.3.8 四边形单元的双向长度坐标

取边长为2的正方形单元为母单元，坐标原点取在正方形中心，四边的坐标为ξ=±1，η=±1，于是，整体直角坐标和局部自然坐标的变换关系为

其中，局部自然坐标L_i的各值为

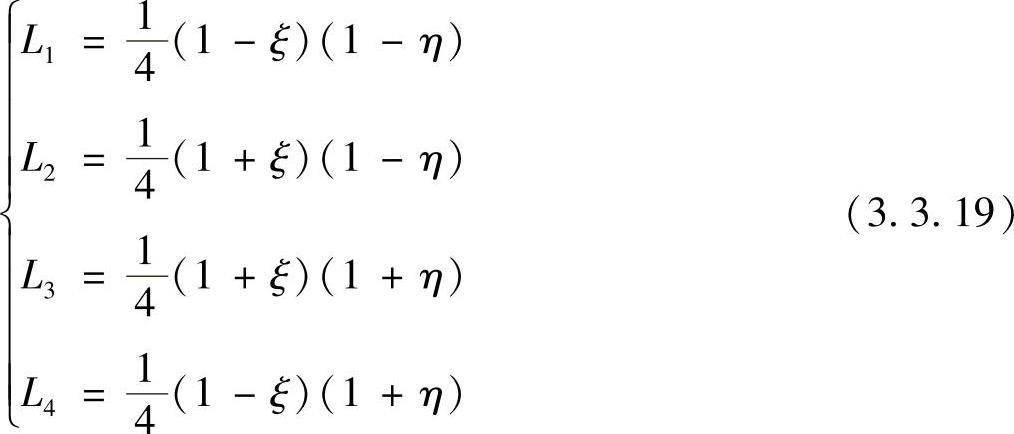
在式（3.3.18）中，若令ξ=1，可得

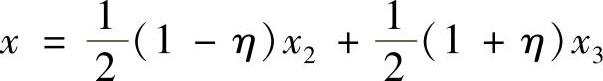
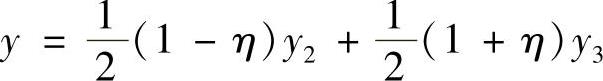
此即边界线23的方程式，同样令ξ=-1，η=1和η=-1将分别得到其他三边的方程式。若令ξ=η=0，则得到

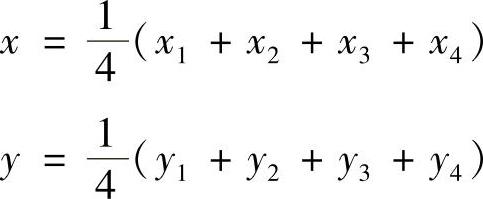
此即四边形的形心，于是，可用等分四边的两族直线分割任意四边形的子单元，以子单元形心为原点，沿ξ和η增大的方向作ξ轴和η轴，得到一个只用在子单元内的局部坐标系（ξ，η），而原来的整体坐标系（x，y）适用于所有单元的整体。通过坐标变换，可以确定（ξ，η）和（x，y）之间的对应关系。总体坐标与局部坐标的变换关系为

由复合函数求导法则推出函数u的导数变换关系

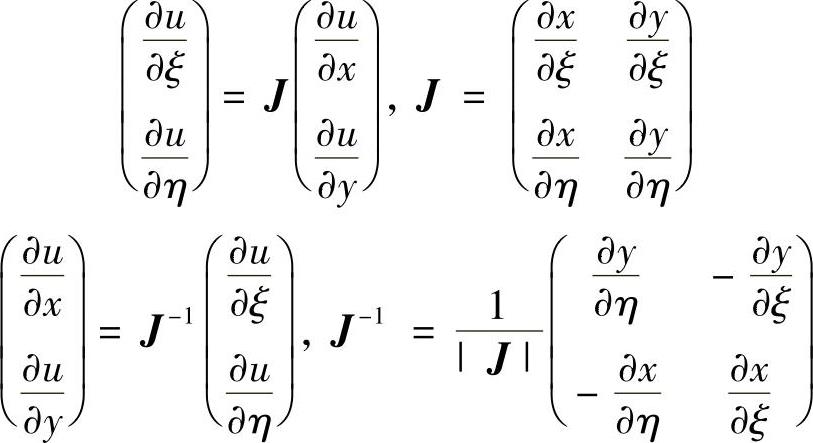
式中，

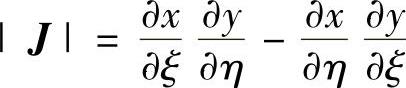
J称为雅可比矩阵，|J|称为雅可比行列式。

以下我们讨论曲线坐标系中的微元积分，可以证明

dA=|J|dξdη

如图3.3.9所示，设ξ，η的单位切向量分别为g和k，则有

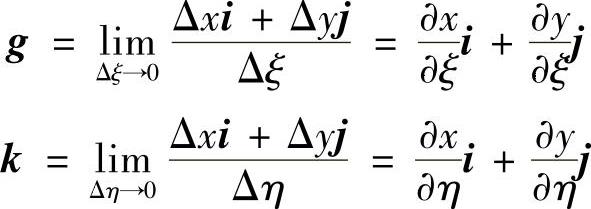
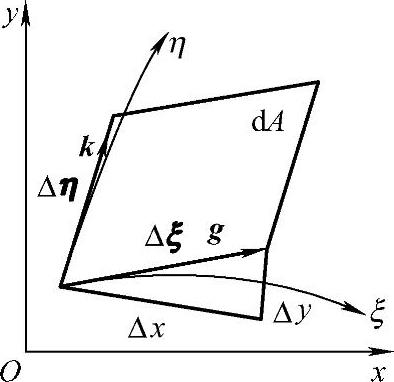
图3.3.9 曲线坐标系 中的微元微分

在曲线坐标系中，微元面积dA等于边长为Δξ和Δη的平行四边形的面积，即

dA=ABS（Δξ×Δη）

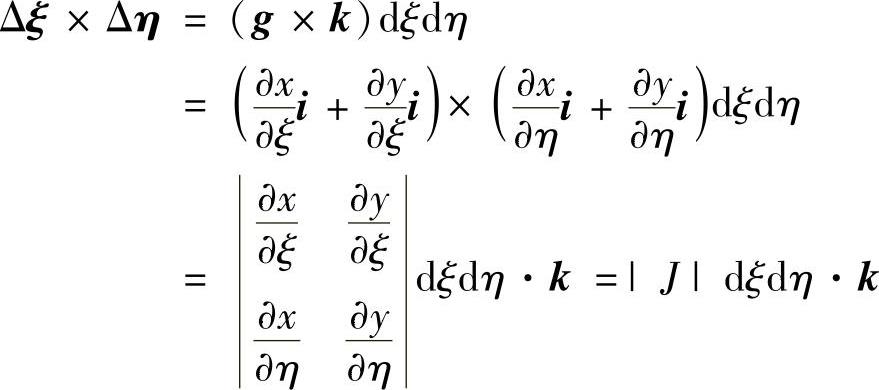
于是

dA=|J|dξdη

即

dxdy=|J|dξdη

4.体积坐标

对于图3.3.10所示的四面体单元，单元的自然坐标取体积坐标，单元中任一点P的体积坐标定义为

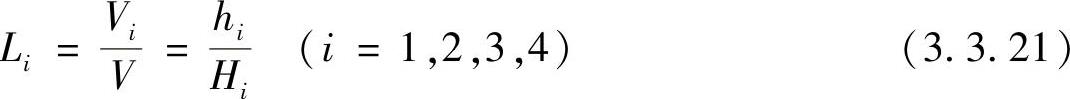
式中，V_i表示点P与结点i所对的底面三角形所构成的四面体的体积；V为四面体单元的体积；而h_i和H_i分别表示点P和结点i到底面的高度。

对于四面体的体积坐标，有

L₁+L₂+L₃+L₄=1 （3.3.22）

其中独立的坐标有三个。

由定义式（3.3.21）可知，对于结点i的体积坐标有L_i=1，而其余结点的体积坐标L_j=0（j≠i）。整体直角坐标和局部自然坐标之间的关系为

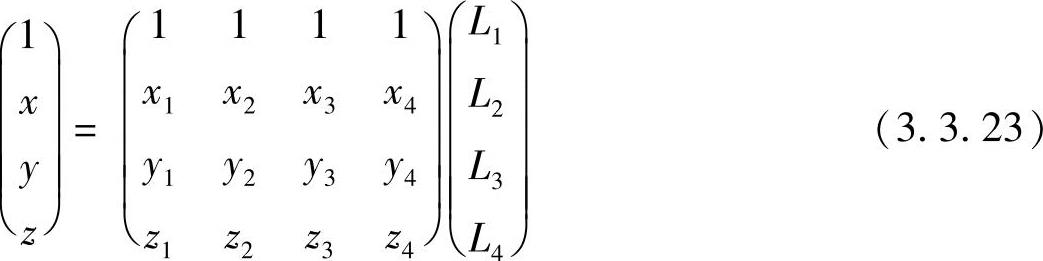
式（3.3.23）也可以写作

L_i=a_i+b_ix+c_iy+d_iz（i=1，2，3，4） （3.3.24）

其中

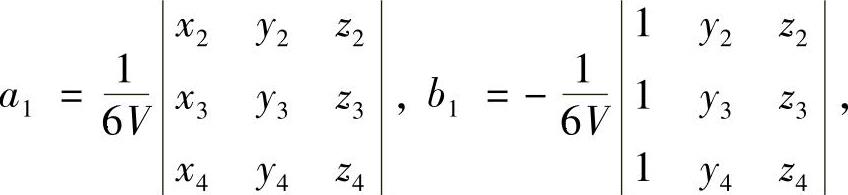
且有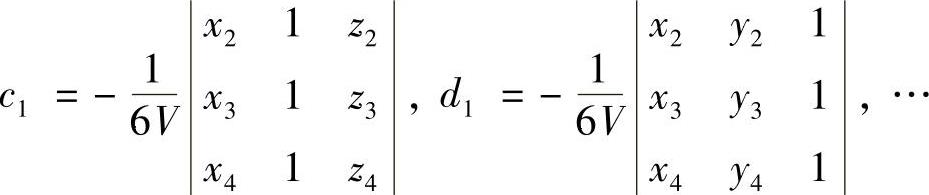

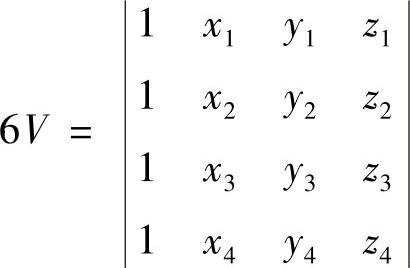
对于其他常数，如a₂，b₂，c₂，d₂，…，可通过轮换下标写出，但应注意符号的正负，如采用右手直角坐标系，对应的结点编号应按如图3.3.10所示，即由结点4看过去，结点1，2，3应按逆时针编号。

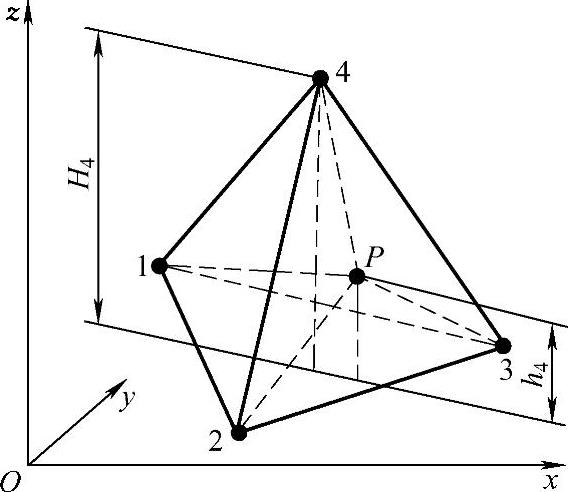
图3.3.10 四面体单元的体积坐标

与二维三角形单元相似，任意四面体单元通过式（3.3.23）的变换关系都可以变换为体积坐标系中的直角四面体单元，该直角四面体单元即为四边体的母单元，如图3.3.11所示。

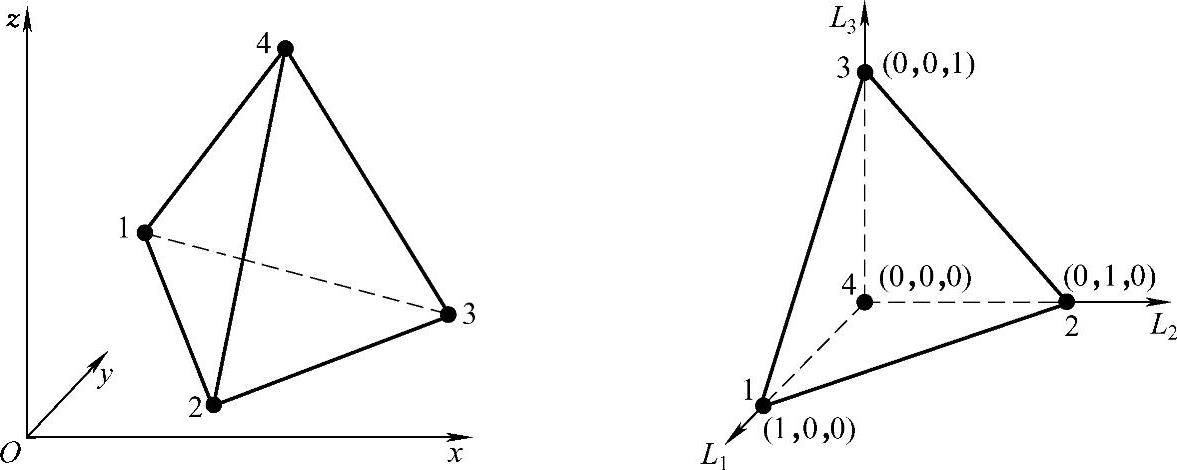
图3.3.11 任意四面体单元变换为直角四面体单元

由式（3.3.24）可得到求导公式为

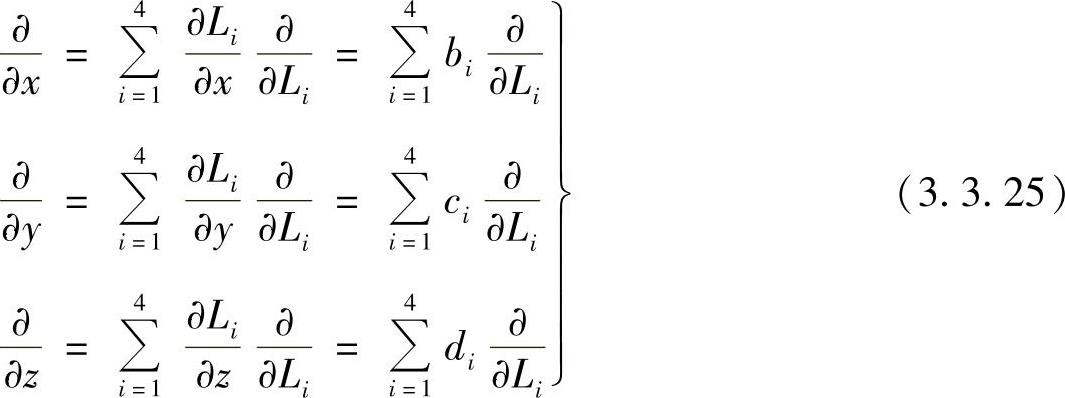
采用四面体体积坐标的多项式各项积分按下式计算

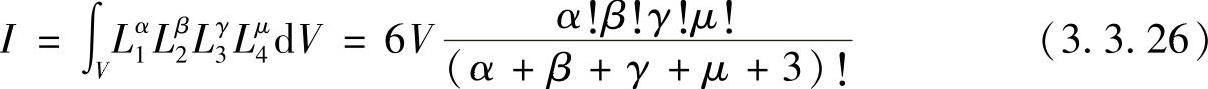
表3.3.3给出了该公式的常用积分值。

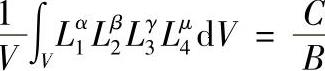
表3.3.3 体积坐标的积分

5.三向长度坐标

仿照二维四边形单元，对任意六面体单元可建立三向长度的自然坐标系，如图3.3.12所示。三维母单元是（ξ，η，ζ）坐标系中的2×2×2的正六面体。局部坐标原点取正六面体的中心、单元的六个平面分别为ξ=±1，η=±1，ζ=±1，在六面体内整体坐标和局部坐标之间的变换关系为

其中，

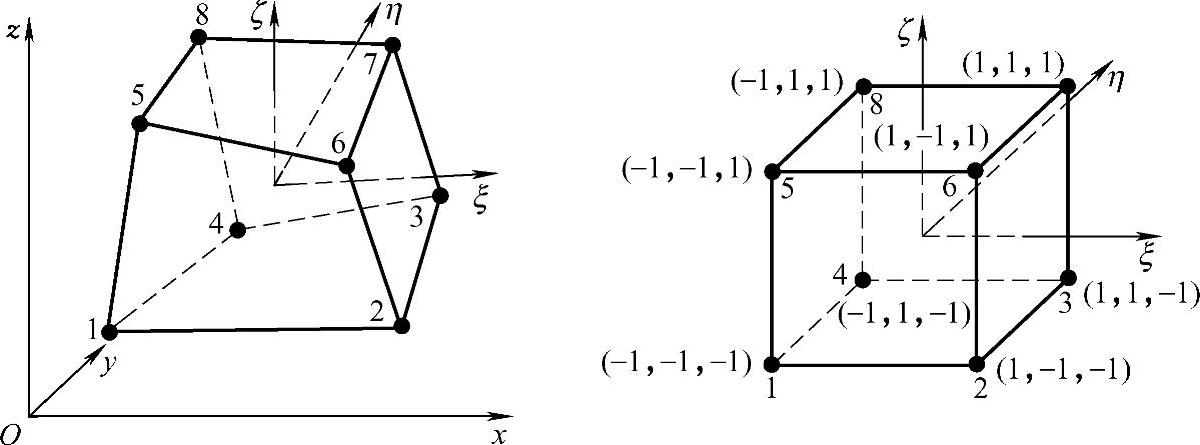
图3.3.12 六面体单元的三向长度坐标

通过与二维四边形单元相似的分析，取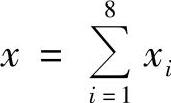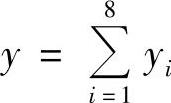，，即取子单元六面体的形心为局部坐标系的原点，沿ξ，η，ζ增大的方向作ξ轴，η轴和ζ轴，得到只用于子单元的局部坐标系（ξ，η，ζ），坐标变换公式（3.3.27）和式（3.3.28）确定了局部坐标系（ξ，η，ζ）和整体坐标系（x，y，z）之间一一对应的关系。

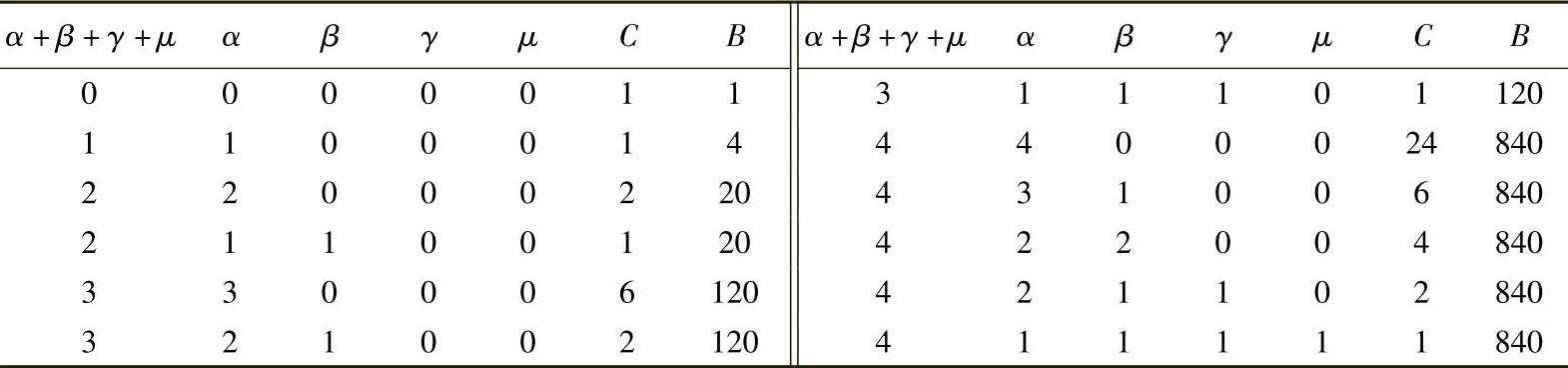
与二维的情况类似，可写出单元对整体坐标的求导数公式为

式中，J是3×3阶的雅可比矩阵，它按照下式用数值方法得到

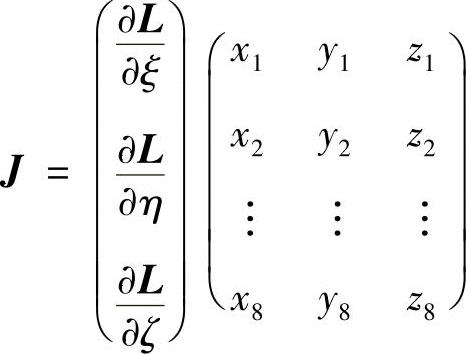
其中，行向量L=（L₁，L₂…L₈），且有

dxdydz=|J|dξdηdζ