有限元法将求解区域剖分为许多单元，我们希望这些单元的几何形状是简单的，能很好地拟合各种求解区域的复杂边界形状，同时又便于在单元内构建近似函数表达式。区域剖分是将求解区域划分成若干互相连接，但不重叠的子区域，这些子区域称为单元。单元的几何形状，可以人为选取，一般是规则的，但形状与尺寸大小可以不同。单元在区域中分布的疏密程度或单元的尺寸大小可根据问题的物理性质决定，通常在物理量变化剧烈的区域，单元尺寸要小一些，排列要密一些。单元划分完成后，再根据对近似函数可微性要求等因素，决定每个单元中结点的数目。除单元的角点一般作为结点外，在单元体边界上或单元内部也可布置结点，每个单元体中的结点数目及排列方式，除少数情形外，一般是相同的。

一维单元一般是直线或曲线上的一个线段，线段上的结点数按基函数插值精度的要求而确定，一般为2个、3个或4个以上。对于有3个及3个以上的结点，其中有2个是和相邻单元相交接的外结点，其他均为内结点，如图3.3.1所示。

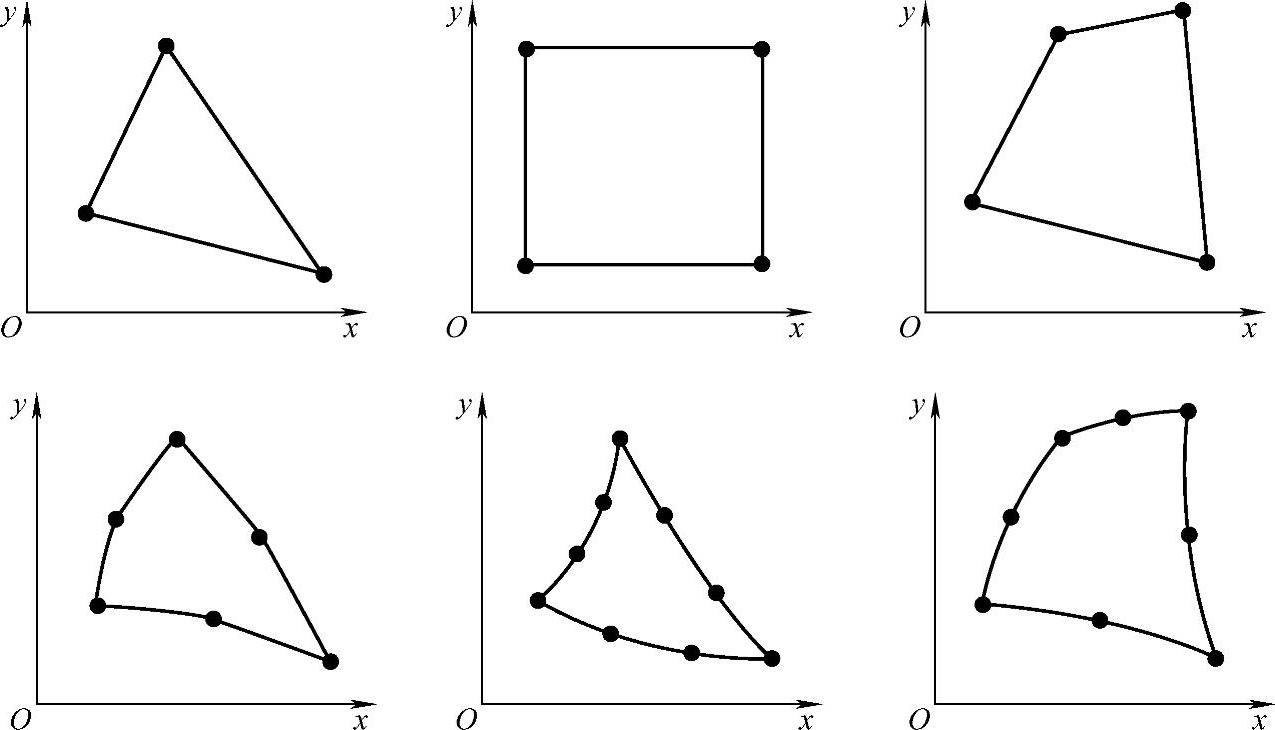
常用的二维单元有三结点的三角形、四结点的矩形和任意四边形直边单元，还有六结点和九、十结点的三角形单元，八结点四边形曲边单元，如图3.3.2所示。

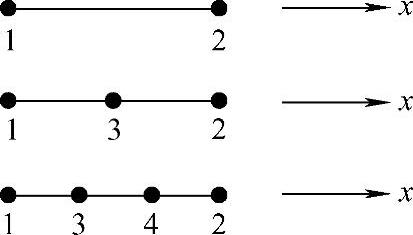
图3.3.1 一维单元

(www.daowen.com)

图3.3.2 二维单元

其中，三结点的三角形单元最简单，应用最普遍，它是二维基本单元，容易对任意形状的二维域进行剖分。四结点的矩形单元形状规则，矩形的边与总体坐标轴平行，便于用计算机自动构造，但不能很好地逼近弯曲的边界。四边形单元可以直接形成，或由两个或四个基本三角形组合而成。这种单元便于对形状不规则的二维域进行剖分，六结点和九、十结点的三角形单元，八结点四边形单元为高次单元，其边界可以是直线的也可以是曲线的，这种单元也便于对不规则的二维区域进行剖分。

三维的单元有四结点的四面体和八结点的正六面体以及一般六面体的直边单元，同样也有十结点或二十结点四面体以及二十结点六面体的直边或曲边单元，如图3.3.3所示，其中，四结点四面体单元类似于二维的三结点三角形单元，是最简单也是应用最普遍的三维基本单元。

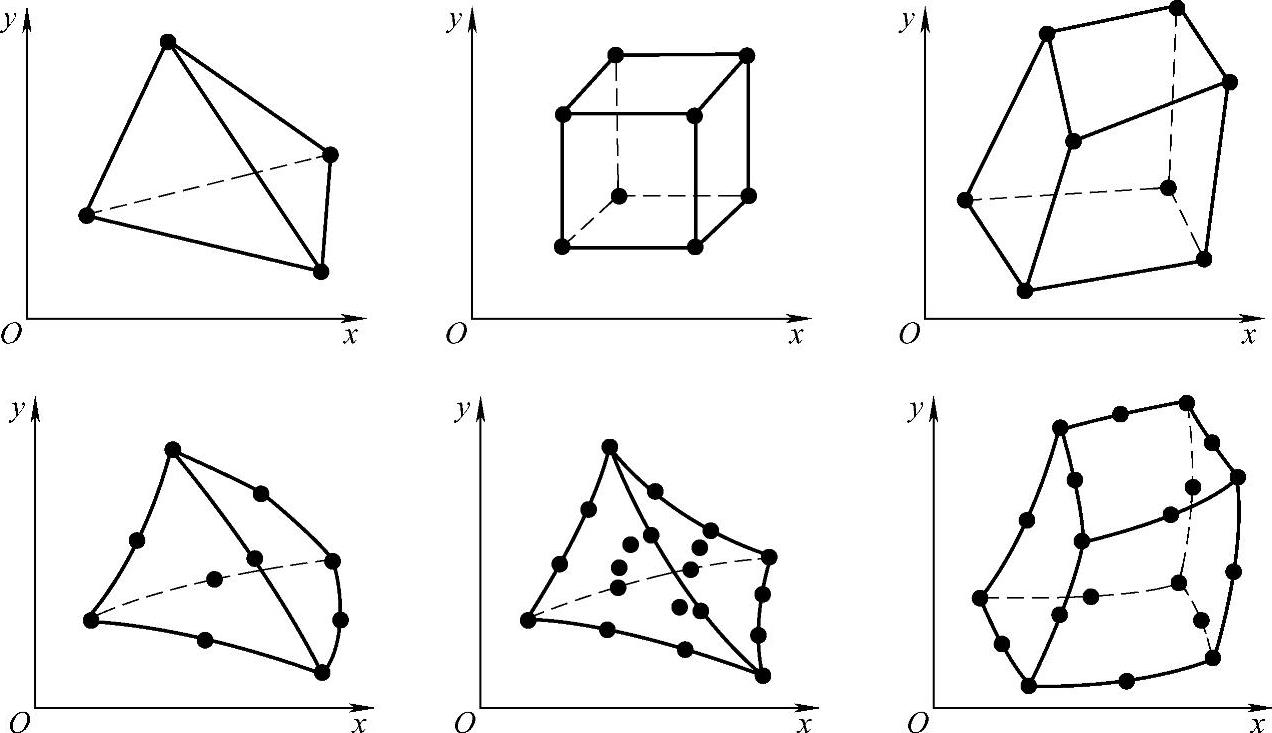
图3.3.3 三维单元