变分问题的有限元法与里兹法本质上相同，它们的差别在于有限元法的近似函数不在整个求解域上，而是在一个单元内定义，它不需要满足问题的全部边界条件。有限元法用简单形状的单元来构成全域的复杂几何形状，然后满足全域的边界条件。所以有限元法比里兹法灵活得多，可以扩充应用于求解各种实际工程所提出的数值计算问题。

考虑边界为Г=Г₁+Г₂的区域D内的偏微分方程边值问题，泛定方程

L（u）=f（在D内） （3.2.1）

和边界条件

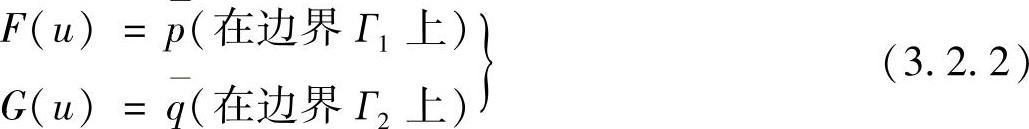
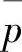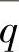方程式（3.2.1）中的L为微分算子，f为独立变量的已知标量函数。边界条件式（3.2.2）中的F是边界Г₁上强加边界条件（狄利克雷边界条件）的微分算子，G为边界Г₂上自然边界条件（诺依曼边界条件）的微分算子，和为给定函数。

对于以上定解问题，若我们能够找到相应的泛函J（u），则根据变分原理，可将求解定解问题转化为求解相应泛函J（u）的极值问题，即由泛函J（u）实现极值的条件去寻找问题的解。

用有限元法求解问题时，将求解的区域划分为若干多个单元，如图3.2.1所示。单元的形式和网格大小应根据具体问题确定，例如，考虑计算域几何形状、计算精度以及计算机容量等条件。

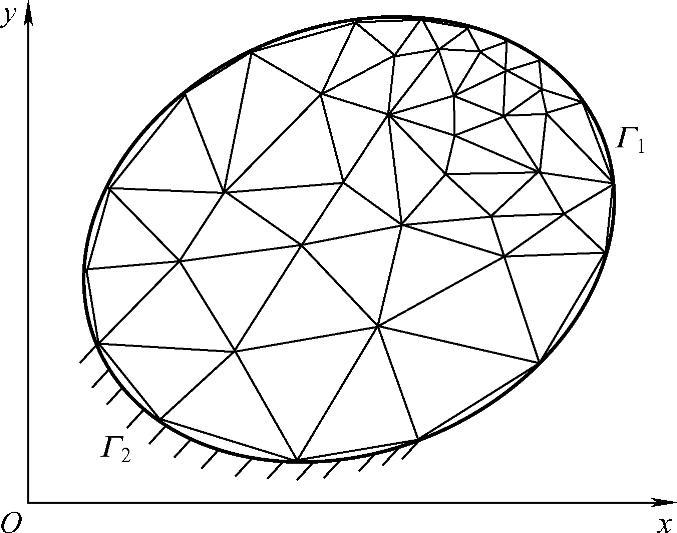
图3.2.1 计算域单元划分

设单元的子域为ΔD，由所有子域构成全域D，即

其中，m为全域的单元数。

将求解区域D划分成m个单元子域ΔD后，全域泛函J（u）可写成各子域的泛函J^e（u）之和，即

使泛函J（u）达到极值的必要条件是使泛函的变分δJ（u）等于零，由式（3.2.4）得

这样就得到建立在变分原理基础上的有限元积分方程。例如，考虑二维拉普拉斯方程

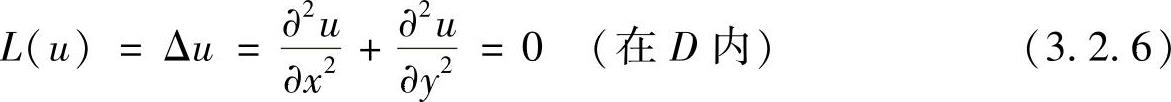
满足边界条件

该问题相应的泛函为

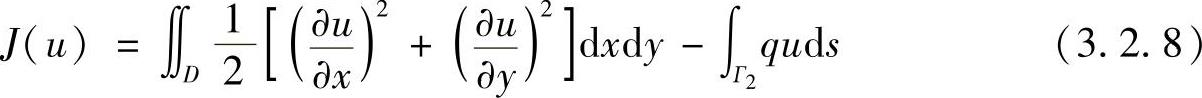(www.daowen.com)

上式可写成各单元子域的泛函之和

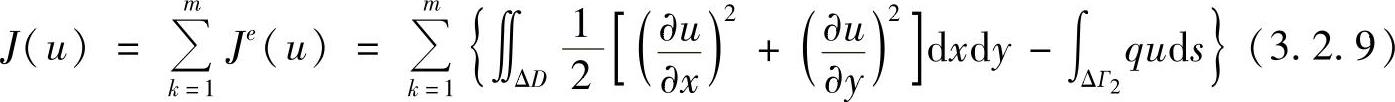
式（3.2.9）中右端第二项为沿Г₂的线积分，只有靠近Г₂边界的单元才有这项积分。

为使泛函达到极值，取泛函的变分δJ（u）等于零，由式（3.2.9）得

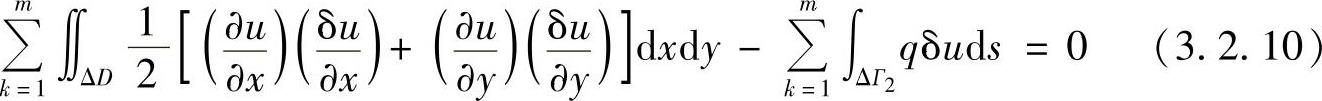
这就是建立在变分基础上求解拉普拉斯方程的有限元积分方程。

在单元内，设函数的近似解为

u=Nu^e（3.2.11）

式中，N为插值形函数；u^e为结点未知值，且

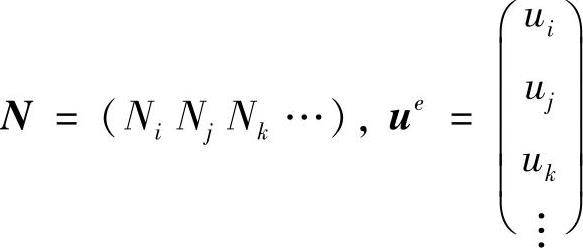
这里的i，j，k，…是单元的结点编号。将式（3.2.11）代入式（3.2.4），得到用结点未知值u^e表示的泛函J^e（u），迭加各单元的泛函J^e（u），便得到全域的包含全部结点未知量u_j（j=1，2，…，n）的泛函

J（u）=J（u₁，u₂，…，u_n） （3.2.12）其中，n为结点未知量个数。

现在的问题变成使泛函式（3.2.12）实现极值来求解各结点未知量u_i，而实现泛函极值的必要条件是使泛函的变分δJ（u）等于零，即

于是

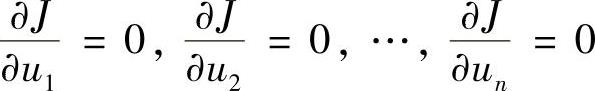
根据式（3.2.4），可得求解变分问题的有限元方程组为

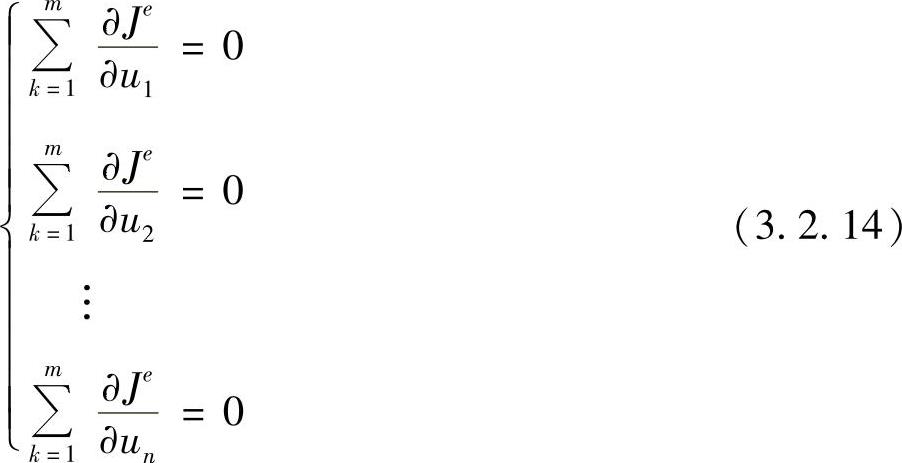
求解方程组式（3.2.14），便得到n个未知值u_i。若将近似解式（3.2.11）代入有限元积分方程，例如，代入求解拉普拉斯方程问题的有限元方程式（3.2.10），则可得到有限元方程组为

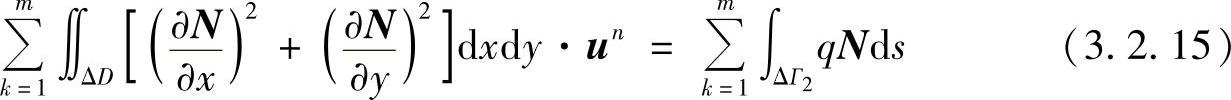
其中，uⁿ是全域的结点未知值；等式左端uⁿ前的积分构成方程组的系数矩阵；等式右端的积分形成右端项。求解式（3.2.15）便可得到所有的未知量uⁿ。

应用求解变分问题的有限元法还必须考虑收敛条件。泛函式（3.2.4）中只包含u的一阶导数项，在选择插值函数时，需保证u的连续性，同时，一阶导数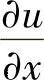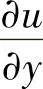，在单元尺寸无限缩小时，应趋于常量，满足这些条件，有限元法得到的解将是收敛的。