基函数的选取与光滑连续导数

在应用加权余量法时，最重要的一步是选取基函数φ_j。一般地，首先要求φ_j能满足问题的边界条件。此外，还要求φ_j（j=1，2，…，N）应是求解域内的一组完备的函数，以使得当N→∞时，近似解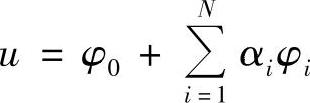收敛于u∗。在选择基函数φ_j时，通常还要考虑以下因素：

1）基函数φ_j计算较容易；

2）待定参数α_j（j=1，2，…，N）容易求得；

3）基函数φ_j具有足够的灵活性；

4）近似解能达到可接受的精度；

5）近似解便于应用。

基函数在求解区域内应是连续的，且足够光滑，即具有足够阶数的连续导数。通常取线性无关的多项式、三角函数、指数函数等作为基函数。例如，对于一维问题（0≤x≤l），若问题的边界条件都是第一类的，即

u_x=0=u₀，u_x=l=u₁

考虑到基函数φ_j（j=1，2，…，N）必须满足对应的齐次边界条件，即

φ_j（0）=0，φ_j（l）=0

故可取

φ₁（x）=x（l-x），φ₂（x）=x²（l-x），…，φ_N（x）=x^N（l-x）

若问题的边界条件是第二类或第三类的，即

u′（0）-h₁u（0）=u₀，u′（l）-h₂u（l）=u₁

则基函数φ_j（j=1，2，…，N）可取为

φ₁（x）=x²（l-x）2，φ₂（x）=x³（l-x）2，…，φ_N（x）=x^N+1（l-x）²

对于二维问题，若问题的边界条件都是第一类的，即

u_Γ=ψ（x，y）

此时，能若找到一函数ω（x，y），且满足条件

则基函数φ_j就可取作

φ₁（x）=ω，φ₂=ωx，φ₃=ωy，φ₄=ωx²，φ₅=ωy²，…

这样，问题归结为确定满足该条件式的函数ω（x，y）。对此，当边界Γ曲线的方程为

F（x，y）=0(https://www.daowen.com)

时，可取

ω（x，y）=±F（x，y）

例如，对于圆心在圆点，半径为r的圆域，边界Γ的方程为

F（x，y）=x²+y²-r²=0

此时，可取

ω（x，y）=x²+y²-r²

若边界Γ是由n条连续曲线分段组成，则这些曲线段的方程分别为

F₁（x，y）=0，F₂（x，y）=0，…，F_n（x，y）=0

则可令

ω（x，y）=F₁（x，y）F₁（x，y）…F_n（x，y）

又如，二维泊松方程第一边值问题

若问题的求解域D为

-a＜x＜a，-b＜y＜b

因为边界Γ的方程为

x=±a和y=±b

于是可令

ω（x，y）=（a²-x²）（b²-y²）

基函数φ_j（x，y）为

也可令

若问题的求解域D是由下列两个圆围成的区域

则取

对于第二、第三类边界条件的情形，这里不作一般讨论。