若令方程余量和自然边界上余量加权积分的线性组合为零，则由此产生的积分表达式，称为强解积分表达式。一般情况下，方程余量加权积分和边界余量的加权积分的线性组合都采取最简单的线性组合形式，即相加或相减，取相加还是相减取决于数学或物理上的方便与否。数学上的考虑是指方程余量的加权积分经分部积分运算以后，可与边界余量的加权积分的一部分相抵消，物理上则反映求解区域内部物理量只能按某种方式相结合使之达到平衡。仍以上面的二阶常微分方程的边值问题式（2.5.1）～式（2.5.3）为例。强解积分表达式为

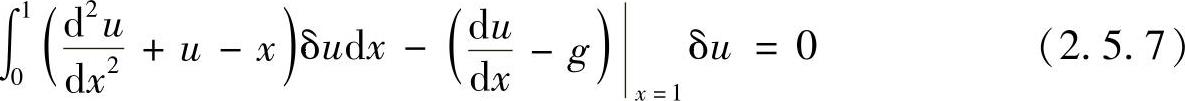
之所以将方程余量加权积分减去边界余量加权积分，是为了便于式（2.5.7）的简化。事实上，对式（2.5.7）进行分部积分，并注意到δu_x=0=0，有

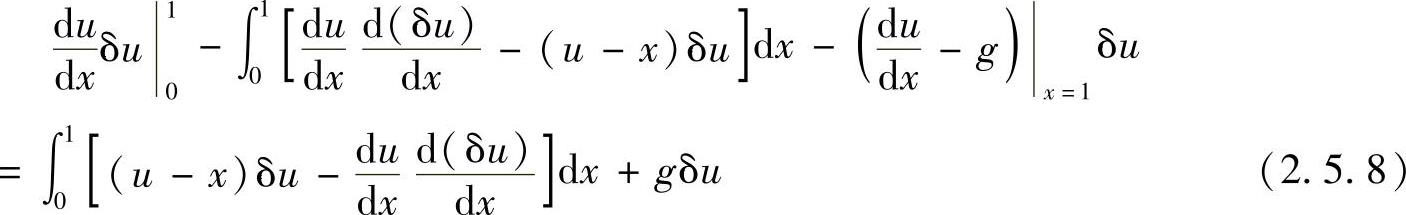
从形式上看，由强解表达式所导出的式（2.5.8）和弱解表达式（2.5.5）完全相同，它们的区别主要反映在强解积分表达式（2.5.8）是伽辽金法求解的出发点，对近似解

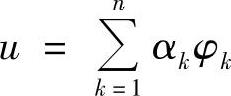
中基函数的要求比弱解积分表达式的要强一些。按式（2.5.7）的要求，基函数φ_k应具有二阶导数可积的光滑程度，这比弱解所要求的一阶导数平方可积的要求要强一些。

在应用伽辽金法求解问题时，由式（2.5.5）和式（2.5.8）表示的两种积分表达式都可以采用，此时自然边界条件在表达中自动满足，只要求近似解满足强加边界条件，因弱解积分表达式比较简单，所以经常取弱解积分表达式进行计算。例如，对于平面渗流问题

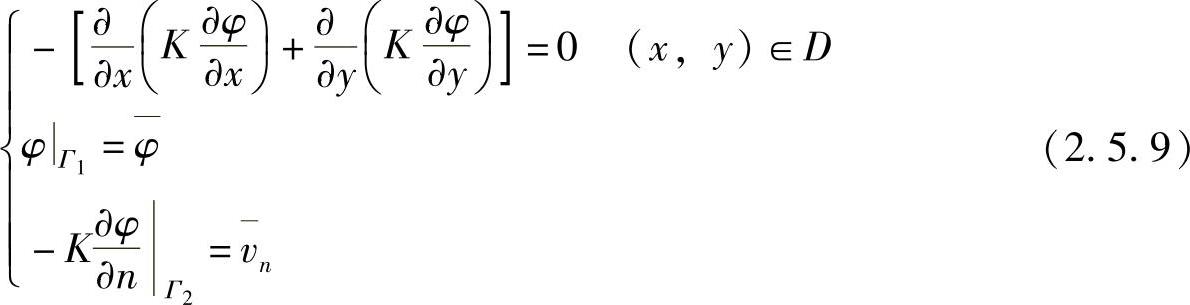
式（2.5.9）第二式为强加边界条件，第三式为自然边界条件。

为了得到弱解积分表达式，我们从伽辽金积分表达式出发，利用高斯公式，有

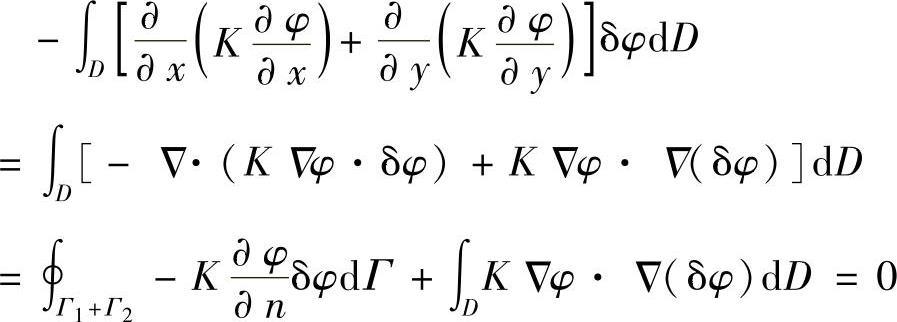
注意到在Γ₁上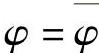，δφ=0；在Γ₂上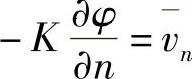，于是，有

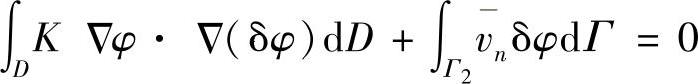
或写成

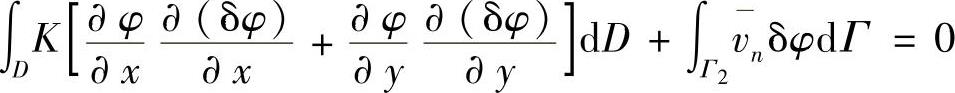
此即伽辽金弱解的积分表达式。

强解的积分表达式可直接写出

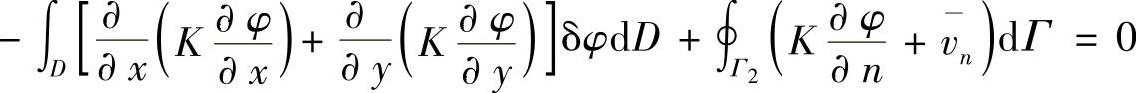
我们讨论下面的二阶常微分方程边值问题的求解

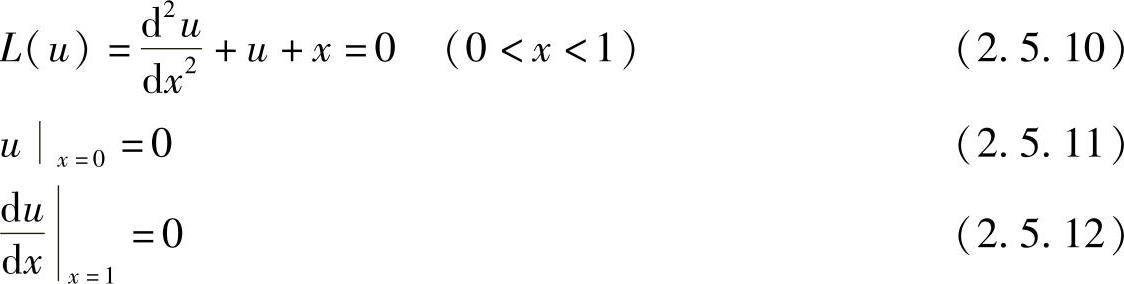
伽辽金积分表达式为

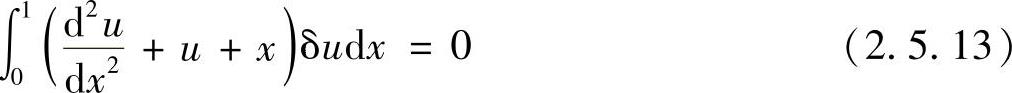
对式（2.5.13）进行分部积分，得到弱解积分表达式

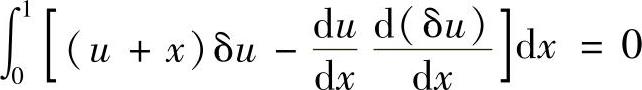
取基函数φ₁=x，φ₂=x²，…，取二级近似，令

u₂=α₁x+α₂x²

它显然满足强加边界条件式（2.5.11）。将近似函数代入弱解积分表达式，得

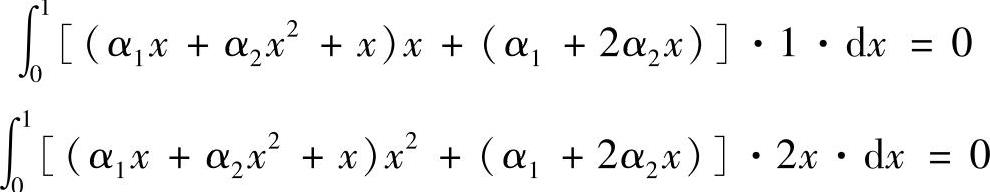
积分后，得

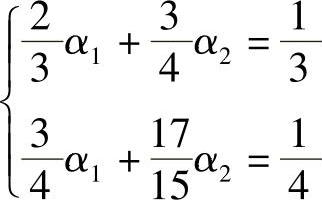
该二元一次方程组解为

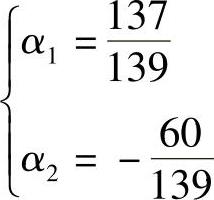
于是，得到近似解

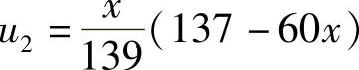
若直接采用伽辽金积分表达式，则此时对近似函数要求比较苛刻，它必须同时满足强加边界条件式（2.5.11）及自然边界条件式（2.5.12）。对于本例这个较简单的情况，可以较容易地选取近似解

它显然符合两个给定的边界条件。代入积分表达式，有(www.daowen.com)

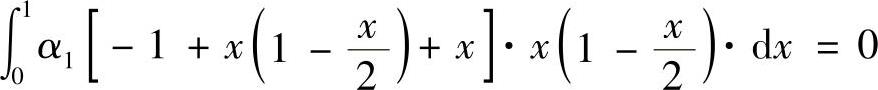
积分后，得

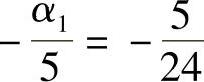
于是，得

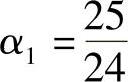
近似解为

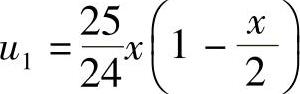
本定解问题的解析解为

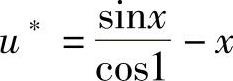
解析解以及强解和弱解的计算结果列于表2.5.1。

表2.5.1 解析解以及强解和弱解的计算结果

下面我们讨论柱坐标系中一维导热拉普拉斯方程边值问题，如图2.5.1所示。定解条件为

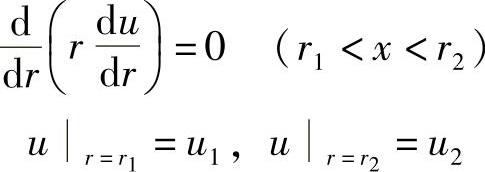
这是一个轴对称圆管壁内稳态热传导方程，u为温度，内壁面和外壁面分别给定温度u₁和u₂。一般地，边界上也可给定热流量，即给出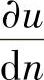的值。给定温度的边界条件是强加边界条件，给定热流量的是自然边界条件。

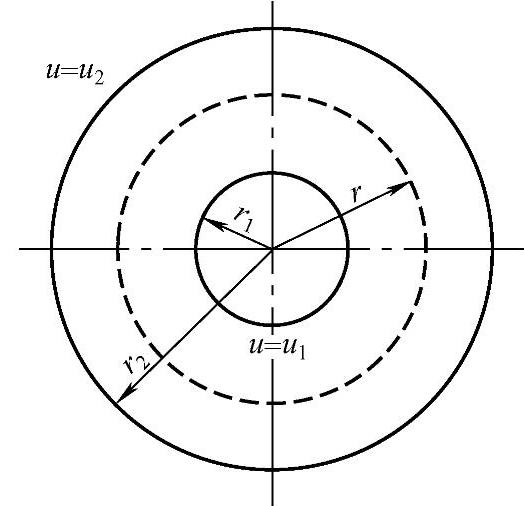
图2.5.1 柱坐标系一维边值问题

先写出伽辽金积分表达式

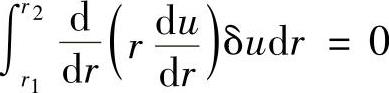
进行分部积分，并注意到在边界上δu=0，因此有

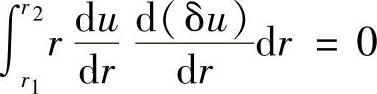
这就是伽辽金弱解表达式。

设近似解为

u=u₀+α₁φ1

其中，u₀应是满足非齐次边界条件的特解，假定它是一个线性函数

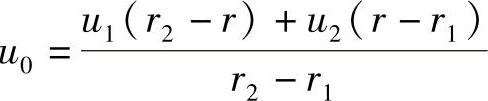
而φ₁是基函数，它应满足齐次边界条件，即在r=r₁及r=r₂处，φ₁=0，符合这个条件的最简单的多项式函数应是

φ₁=r₁r₂-（r₁+r₂）r+r²

于是，近似解成为

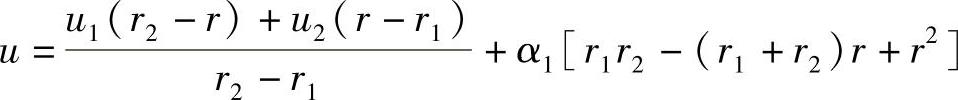
其中，α₁是待定系数。将上式代入伽辽金弱解表达式中，可求得

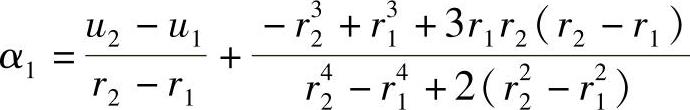
于是得到方程的一级近似解，即

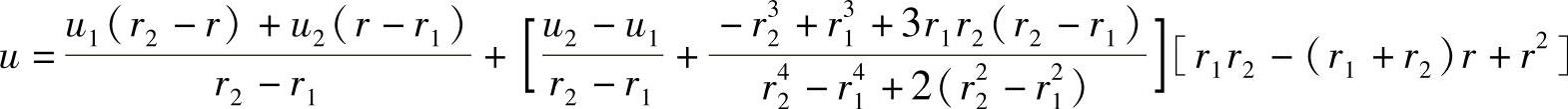
本问题是传热学中的经典问题，其解析解为

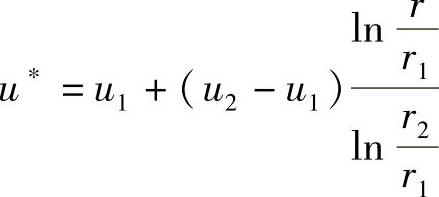
请读者通过预设u₁，u₂，r₁和r₂的值，比较一级近似解u与解析解u∗之间的误差。