对伽辽金法的积分表达式（2.5.4）进行分部积分，然后将自然边界条件代入表达式中，以此所获得的积分表达式作为伽辽金法求解的出发点，这对近似函数的连续可微性的要求降低了，但这样的解，一般并不满足算子方程对函数的连续可微性要求，因此称之为弱解，这个积分表达式，就称为弱解积分表达式。将式（2.5.4）进行分部积分，有

代入式（2.5.2）的强加边界条件，u_x=0=f为给定常数，得δu_x=0=0；将式（2.5.3）的自然边界条件代入，即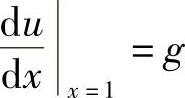，得

积分式（2.5.5）即为弱解积分表达式。

以弱解积分表达式（2.5.5）作为求解的出发点，设近似解为

u=α_kφ_k （2.5.6）(www.daowen.com)

其中，φ_k（k=1，2，…，n）是选定的基函数，它应当满足式（2.5.5）中对它的连续可微性要求，也就是要求φ_k具有一阶导数平方可积就可以了。显然，由此获得的近似解，就连续可微性来说，不一定满足方程式（2.5.1）的要求，从这个意义上来说，它是一个广义解，称为弱解。

另一方面，积分表达式（2.5.5）已自动满足了自然边界条件式（2.5.3），因此，只要近似解式（2.5.6）满足强加边界条件（2.5.2）即可。那么，为什么说式（2.5.5）自动满足自然边界条件呢？事实上

由于δu是u的任意增量，因此由上式可得

可见，自然边界条件已满足，但对于x=0处u的取值，式中并没有反映出来，这就要求近似解式（2.5.6）必须满足强加边界条件式（2.5.2）。