以二维为例，设泛函J（u）所依赖的函数u（x，y）具有如下近似形式

其中，φ_i为一组满足边界条件的线性独立函数系列，称为坐标函数，或基函数，α_i为待定参数。这里的近似解式（2.3.1）称为试探函数，或称为近似函数。如将式（2.3.1）代入泛函表达式，则泛函J（u）就变成参数α_i的函数，即

J（u）=J（α₁，α₂，…，α_n）

根据多元函数实现极值的必要条件，泛函J（u）在函数u（x，y）上实现极值应使参数α_i满足

解出未知参数α_i，并将它们代入式（2.3.1），即得所要求的近似解

u（x，y）=u（x，y，α₁，α₂，…，α_n）

以下对里兹法作简要的介绍。已知微分方程

y″+y+1=0 （2.3.3）

满足边界条件

的精确解为

由式（2.3.5）得

现用变分方法求取近似解，为此作泛函

利用欧拉方程不难证明，式（2.3.6）在满足边界条件式（2.3.4）并取极值时的极值曲线y（x）就是微分方程式（2.3.3）和边界条件式（2.3.3）的解。由于函数y（x）未知，引入试探函数。通常，试探函数取具有良好微分性能的初等函数多项式，以便于进行微分和积分运算，且试探函数需满足边界条件。这里，取满足边界条件式（2.3.4）的试探函数，如

y=α₁（x-x²）+α₂（x-x³）+α₃（x-x⁴）+… （2.3.7）

y=α₁sinπx+α₂sin2πx+α₃sin3πx+… （2.3.8）

显然，试探函数的项数取得越多，达到的精度就越高。若取n项，则有α₁，α₂，…，α_n，计n个未知量。将多项式代入泛函式（2.3.6）后，泛函J[y（x）]实际上成为J（α₁，α₂，…，α_n）的多元函数，于是变分问题转化为多元函数求极值的问题，即

式（2.3.9）为n个代数方程，可解出α₁，α₂，…，α_n这n个未知量。(www.daowen.com)

作为简单介绍，只取多项式（2.3.7）的第一项，即取

y=α₁（x-x²） （2.3.10）

代入式（2.3.6），得

由多元函数取极值的条件，得

所以

于是，得

代入式（2.3.10），得

这就是极值曲线的近似解。由式（2.3.11），得

若采用式（2.3.8）的试探函数作变分计算，取前三项，则

y=α₁sinπx+α₂sin2πx+α₃sin3πx （2.3.12）

考虑到函数列{sinnπx}和{cosnπx}的正交性，以及

将这些关系及式（2.3.12）代入到式（2.3.6），有

由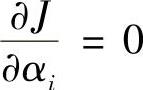（i=1，2，3），得

于是，得

当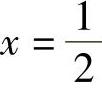时，y=0.1384（精确解为y=0.1395）

比较这两次计算可以看出，选择试探函数非常重要，后者由于试探函数选择不当，作三项计算的精度还不如前者作一项计算的精度来得高。可见，里兹法只是在试探函数族中找一个最优解，求解的精度取决于所选的试探函数。当所选的试探函数满足解的某些已知性质时，就可能改善近似解的精度。若所选的试探函数恰好包含了精确解，则里兹法就可得到精确解。当试探函数是一个无穷序列函数的一部分时，试探函数中包含的函数项数越多，它越接近精确解，并且原则上可以得到任何精度的近似解。