在变分法中还会遇到这样一类问题，即求解域边界的全部或一部分是待定的，这些待定的边界本身也需要在求取泛函极值的同时加以确定，这属于待定边界情形的变分问题。这里只讨论二维和三维待定边界的变分问题。对于二维待定边界泛函

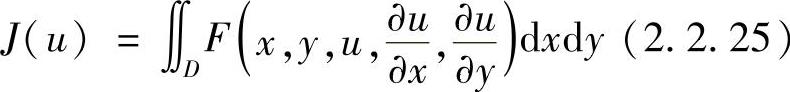
的极值问题。由于边界待定，故泛函J（u）的变分来源于u的变分δu和域的变分δD，有极值条件

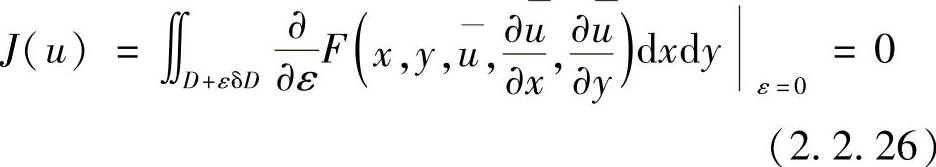
式中，u=u+εδu。上式可分为两部分

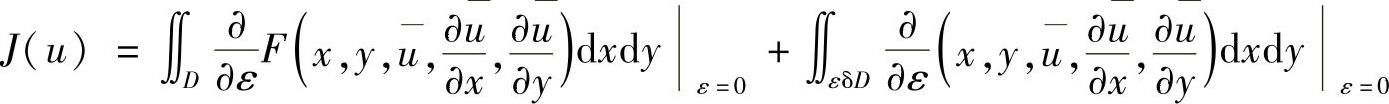
等式右端第一项积分，可得

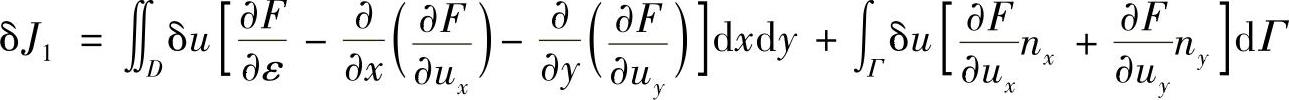
等式右端第二项积分中的δD是域δD在法向n上所开拓的区域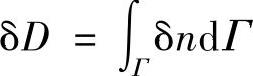，，如图2.2.4所示。

因此第二项变分为

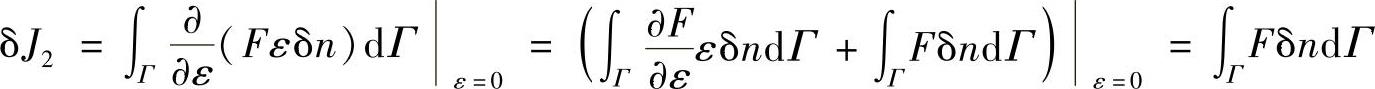
于是得到待定边界变分问题的极值条件为

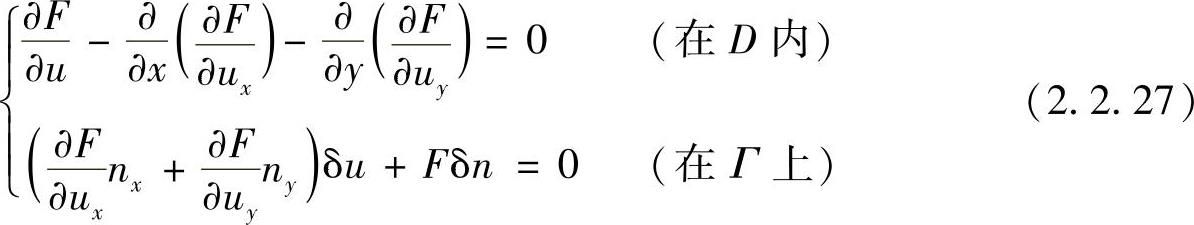
此即待定边界情况下二维问题的欧拉方程。(www.daowen.com)

应用方程式（2.2.27）第二式的边界条件有两种，一种是u值在边界Γ₁上给定，这时δu=0，故对式（2.2.27）的第二式只要求满足

F=0 （在Γ₁上） （2.2.28）

另一种是在边界Γ₂上u未定，这时δu≠0，对式（2.2.27）的第二式要求同时满足下面两个条件

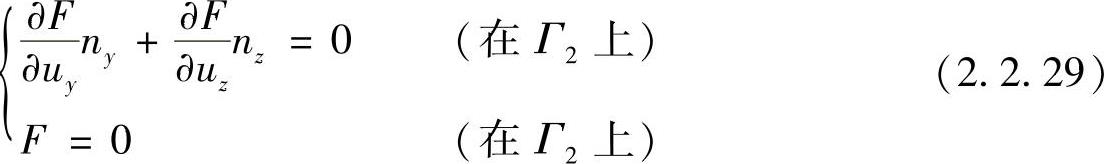
在实际问题中，往往并不是问题的全部边界都是待定的，对于待定的边界部分可采用上述极值条件（2.2.27）的第一式以及式（2.2.28）和式（2.2.29），而对于固定的边界部分则只需满足式（2.2.27）的第一式和式（2.2.29）的第一式。

对于三维待定边界的泛函

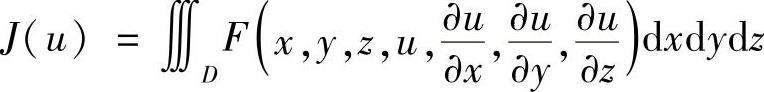
采用相同的方法可推出相应的欧拉方程为

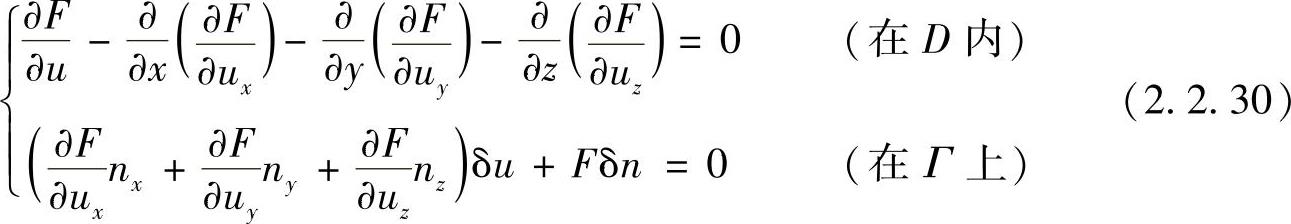
对给定u值的边界Γ₁和未绐定u值的边界Γ₂，式（2.2.30）的第二式改为

F=0（在Γ₁上） （2.2.31）