前面讨论的泛函J[y（x）]，其中y是只包括一个自变量x的函数，本节先讨论的泛函J[u（x，y）]，其中函数u是两个自变量x和y的函数。对于泛函

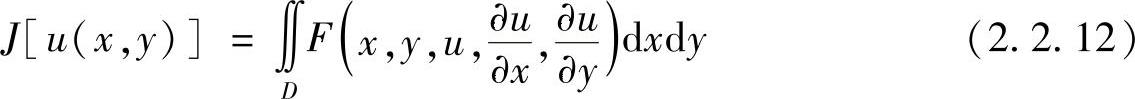
式中，x，y为两个独立变量，是平面两个坐标；u（x，y）是任意连续平面函数，该函数在区域D的边界Г上有已知值，即具有第一类边界条件，如图2.2.1所示的曲面，在这种情况下求泛函取得极值的曲面u（x，y）。

因已知u（x，y）|Г=f，因此这是一个固定边界的变分问题，即泛函J取极值时，极值曲面的一系列邻近曲面在区域D中的值可改变，但在边界上的值不变。与前面介绍的固定端点变分类似，作极值曲面u（x，y）的一系列邻近曲面

u（x，y，ε）=u（x，y）+εη（x，y） （2.2.13）

式中，η（x，y）为在边界Г上函数值等于零的任意光滑连续函数，即η（x，y）|Г=0。ε为一绝对值较小的参变量，并与x和y无关。于是

图2.2.1 边界值固定的平面场

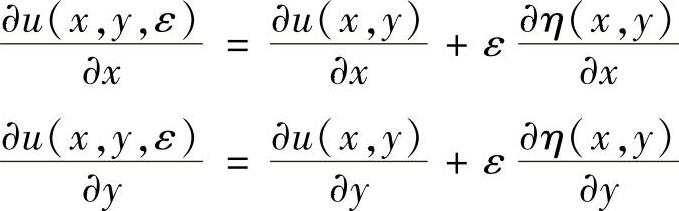
将这些邻近曲面代入式（2.2.12），得

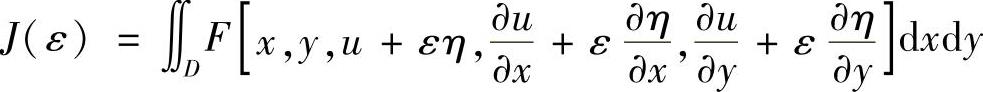
泛函取极值的条件为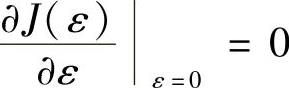，故

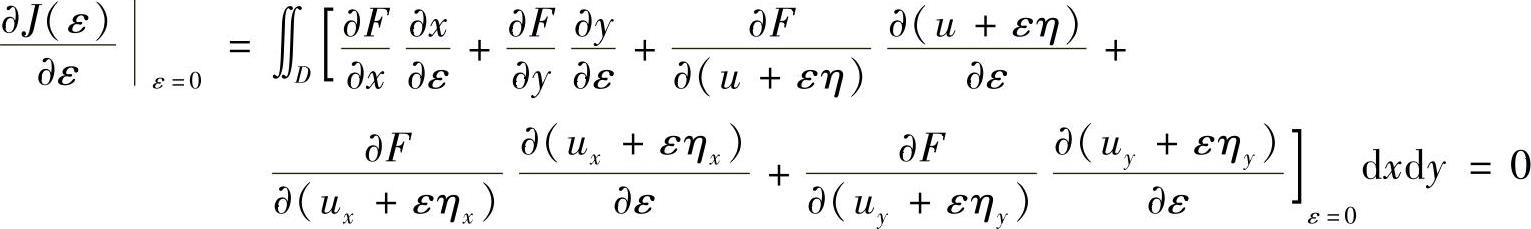
因ε与x，y无关，所以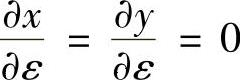，上式简化为

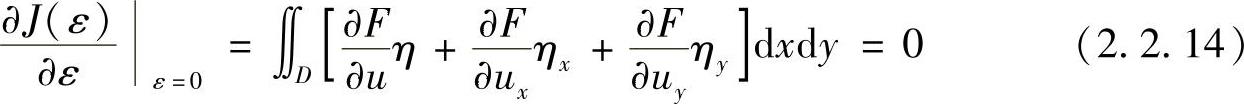
为进一步简化式（2.2.14），可应用格林公式。格林公式的形式为

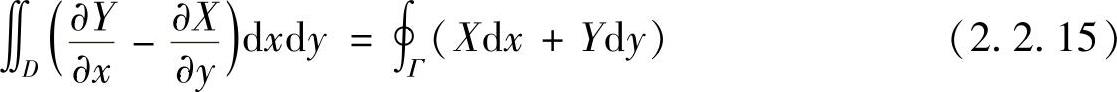
式中，X（x，y）和Y（x，y）是定义在区域D和边界Γ上的两个任意连续函数。取出式（2.2.14）中的后两项

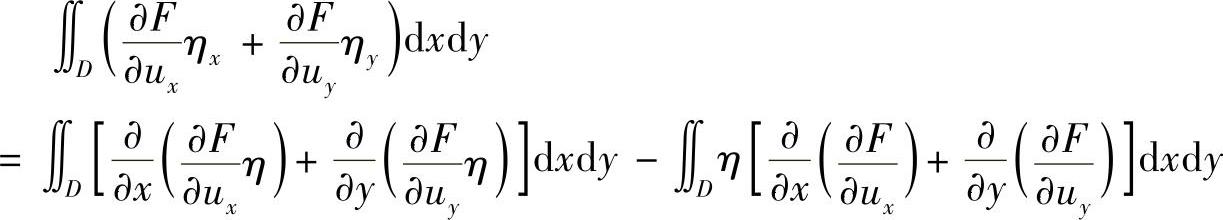
对上式右端的第一个积分式应用格林公式，令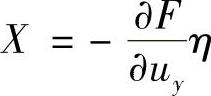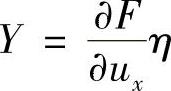，，得

代回式（2.2.14），得

对于固定边界_η（x，y）|_Γ=0，式（2.2.16）成为

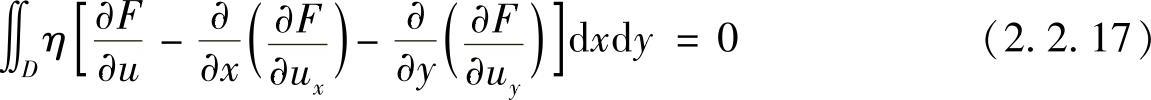
式（2.2.17）中积分值对任意函数η（x，y）都为零，于是，极值曲面u（x，y）必须满足的条件为

式（2.2.18）即为欧拉方程。

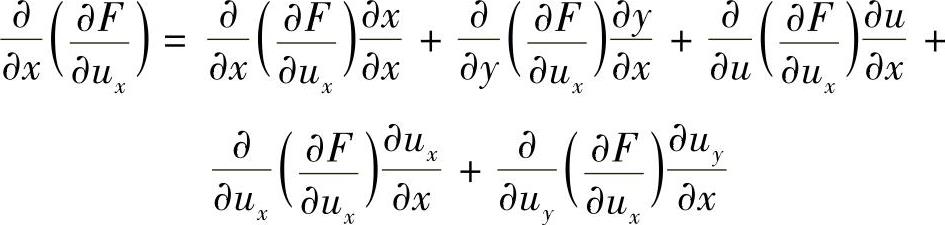
由于x，y为独立变量，因此上式可以简写为

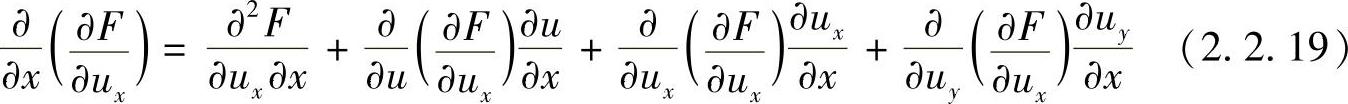
同理得

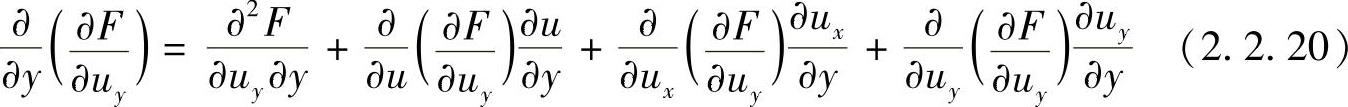
式（2.2.18）是极值曲面必须满足的微分方程，函数在边界Γ上的已知值作为欧拉微分方程的定解条件。

下面考虑一个典型的二维边值问题，求泛函

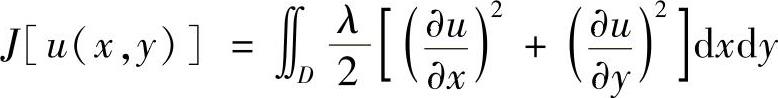
的极值曲面为u（x，y），其中，曲面u在域D的边界Γ上的温度值为已知，即

u（x，y）|_Γ=f（x，y）

应用欧拉方程式（2.2.18），其中

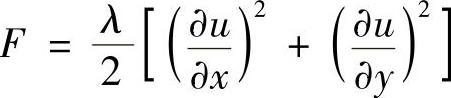
注意到F中不包含x，y和u，代入式（2.2.19）和式（2.2.20），得

因此

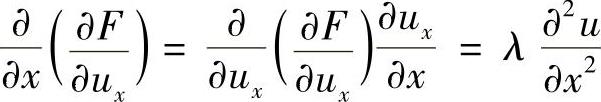(www.daowen.com)

而

于是

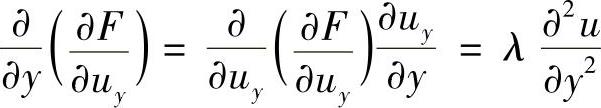
代入欧拉方程式（2.2.18），得

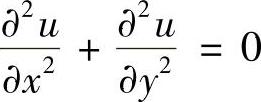
可见，极值曲面为满足拉普拉斯方程的一系列曲面，为了确定唯一的极值曲面，必须利用固定边界给出的定解条件，这里指定为第一类边界条件，即强加边界条件。

下面我们直接从变分的角度讨论一般二维和三维边值问题的欧拉方程。考虑二维边值问题，设有泛函

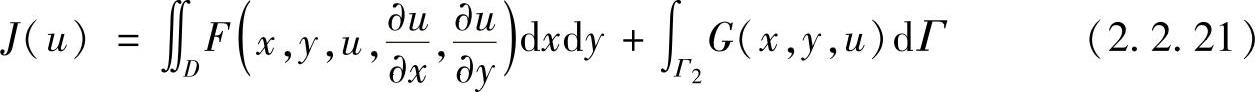
其中，u（x，y），G（x，y，u）是沿边界Γ₂取值的函数。这里假定u在边界Γ₁上的函数值是给定的，在边界Γ₂上是未定的，如图2.2.2所示。

假定泛函J[u]存在，并在u=u（x，y）上实现极值，在极值曲面u（x，y）的邻域，函数可写成

在边界Γ₁上，有δu（x，y）=0。于是，式（2.2.21）成为

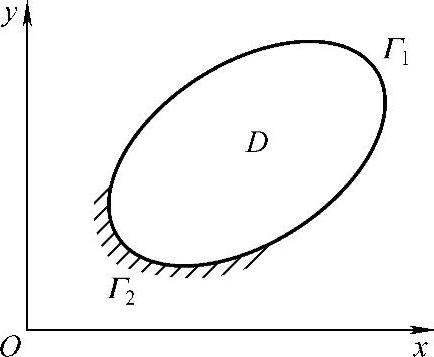
图2.2.2 二维边值问题

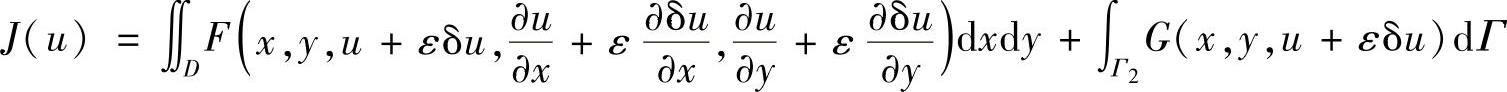
上式的泛函为参数ε的函数。由积分符号下求微分的方法，得到

当ε=0时，有

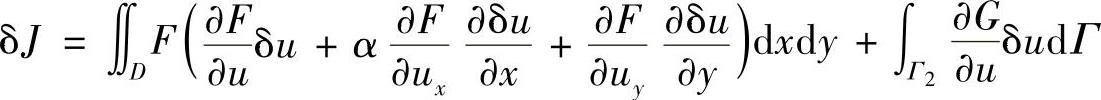
再由部分积分

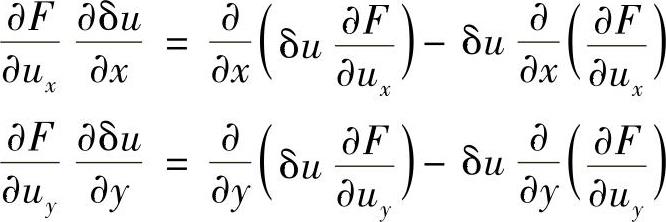
于是

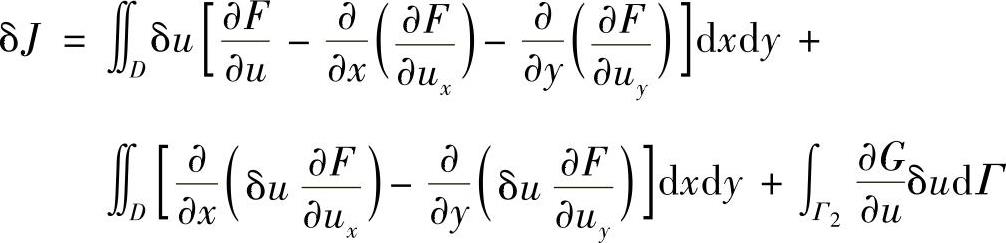
令上式右边第二项中的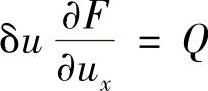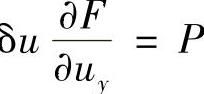，，根据格林公式

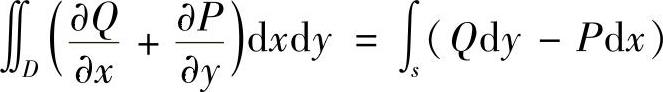
有

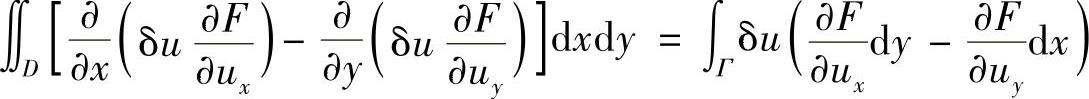
其中，Γ=Γ₁+Γ₂。考虑到边界Γ₁上的δu=0，上式右边只剩下沿边界Γ₂上的线积分。在边界上dy=n_xdΓ，dx=-n_ydΓ。这里n_x=cos（n，x），n_y=cos（n，y），为边界外法线的方向余弦。于是，有

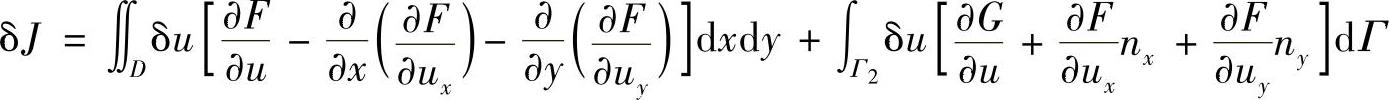
考虑到δu在域D内和边界Γ₂上都是任意的，要使泛函的变分δJ=0，必须使得下面的两式成立

此即二维问题的欧拉方程。因此，由式（2.2.21）所给的泛函，如在u=u（x，y）上取得极值，函数u（x，y）必须满足欧拉方程式（2.2.22）。

用同样的方法可以推导出三维的欧拉方程。设函数u=u（x，y，z）为空间域D（x，y，z）内的连续二阶可微函数，u在边界Γ₁上u=u₁为已知的，在边界Γ₂上为未知的，如图2.2.3所示。对于泛函

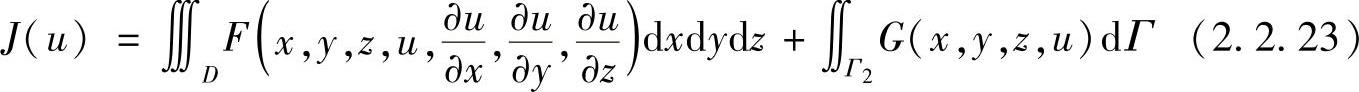
应用推导二维问题欧拉方程相同的方法，可导出三维问题的欧拉方程。

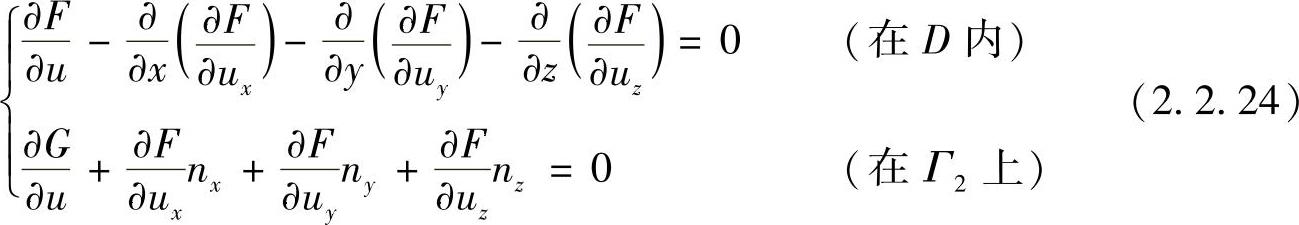
式中，

n_x=cos（n，x），n_y=cos（n，y），n_z=cos（n，z）为边界外法线的方向余弦。因此，在三维问题中，由式（2.2.23）表示的泛函J（u），如果在u=u（x，y，z）上取得极值，则函数u=u（x，y，z）必须满足欧拉方程式（2.2.24）。

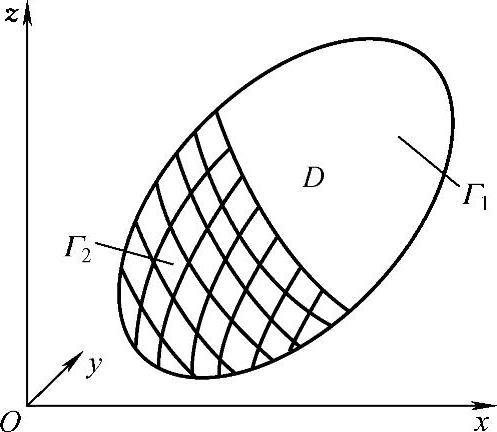
图2.2.3 三维边值问题

图2.2.4 可变域变分