除了前文介绍的两端点固定的变分问题外,还有极值曲线的一端或两端可在已知曲线上移动的变分问题,称为可动端点的变分问题。例如,在前面讨论的最速下降线问题中,如图2.1.2所示,点A固定不动,点B可在x2=a的竖直线上移动。当点B在任一给定位置时都可得到一条极值曲线,这就是固定端点极值曲线。所谓可动端点变分问题,就是对上述这些极值曲线上再作一比较,以求出B在哪一高度时的降落时间最短。所以,可动端点的极值曲线是从一系列固定边界的极值曲线中挑选出来的,因此,固定端点极值曲线应该满足的欧拉方程,在这里仍应满足。
可动端点的变分问题与固定端点的变分问题基本相同,仍要对泛函求极值曲线,差别在于极值曲线必须满足的边界条件中,只有y(x1)=y1。由于点B的y坐标不固定,因此,作比较函数时,所选用的任意光滑连续η(x),只有η(x1)=0,而η(x2)≠0。经过与上述类似的变分推导后得到
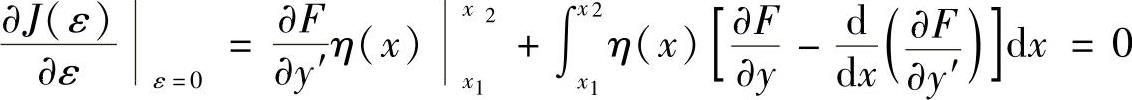
这里η(x1)=0,η(x2)≠0,于是,上式成为
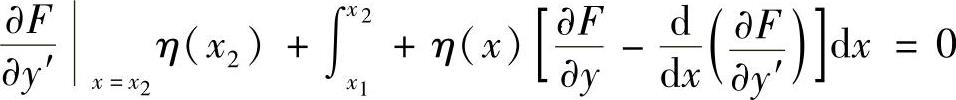
因欧拉方程必须满足,即
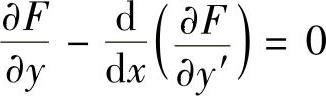
这样就得到

式(2.2.11)称为自然边界条件。欧拉方程是极值曲线必须满足的条件,求解欧拉微分方程可得两个积分常数,利用边界条件y(x1)=y1可以确定一个,另一个由式(2.2.11)的自然边界条件来确定。例如,对于最速下降线问题。若求从原点(0,0)自由下滑到直线x2=a,前面已得到
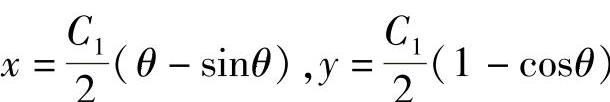
现在仍然有效,在前面的求解过程中,常数C2是已由固定点A(0,0)确定,现用自然边界条件确定C1。由
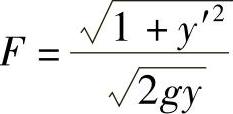
得(https://www.daowen.com)
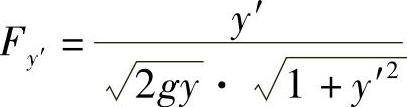
利用式(2.2.11),得y′x=a=0,即
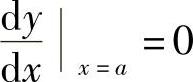
但
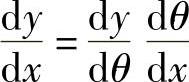
而
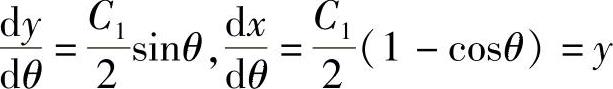
因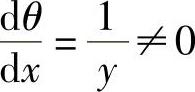 ,故
,故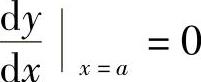 ,于是
,于是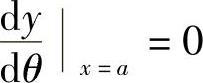 ,即
,即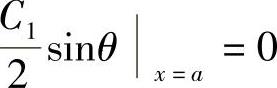 ,又因C1≠0,于是
,又因C1≠0,于是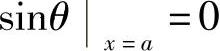 ,有
,有
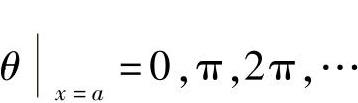
其中,θx=a=0不合理舍去。若取最简值θx=a=π,代入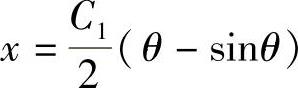 ,得
,得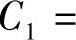
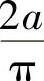 。
。
最终得到极值曲线方程为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







