本节讨论由泛函极值条件推得的微分方程，即欧拉方程。以下求式（2.1.3）中的泛函J取极值时，函数y（x）必须满足的条件。由式（2.1.3）

将y（x）的邻近曲线代入，得

由式（2.1.13），并注意对积分号中函数求导数时应用莱布尼茨法则，即

由此得到

考虑到x与ε无关，并将y（x，ε）与y′（x，ε）的关系代入，得

即

为了进一步简化式（2.2.1），对第二项采取分部积分，其对应于

中的

得

所以

代入式（2.2.1），得

由于_η（x₁）=η（x₂）=0，式（2.2.2）成为

上式的积分值对任意的函数_η（x）都为零，故可推出

式（2.2.4）称为欧拉方程，是极值曲线应该满足的必要条件。欧拉方程是一个微分方程，求解这个微分方程，可得无穷多条极值曲线，再把边界条件代入，即可得到唯一极值曲线方程。

由F=F（x，y，y′），可得式（2.2.4）中全导数的展开式为

最后欧拉方程的形式为

下面讨论两种特殊情况。第一种特殊情况为F中不包含y，即F=F（x，y′），此时欧拉方程式（2.2.5）简化成

首次积分得F_y′=C₁，再积分一次就可得到极值曲线。例如，式（2.1.1）中曲线长度命题，即求连接A和B两点间长度J最短的曲线y=y（x），因F=1+（y′）2，而

于是

解得

再积分一次，得

这显然是一个直线方程。其中，常数C₁和C₂可由边界条件y₀=y（x₀），y₁=y（x₁）确定。C₁和C₂确定后代入上式，经整理，得

由此可见，连接两点的曲线长度最短的曲线是一条直线段。

第二种特殊情况为F中不包含x，即F=F（y，y′），此时欧拉方程式（2.2.5）简化成

可写成全微分的形式

为了证明这一点，只要把式（2.2.7）展开即可，展开第一项，得

展开第二项，得

代入式（2.2.7），得

由于y′≠0，于是得到式（2.2.6）。(www.daowen.com)

由式（2.2.7），积分可得

例如，最速下降线y（x），已知泛函式（2.1.2）

由式（2.2.8），得

所以

利用三角函数的参数方程求解微分方程式（2.2.9），为此，记

代入式（2.2.9），得

再求x的参数方程，由

为了消去dy，可将式（2.2.10）取微分后代入，得

故

积分后得

由y（0）=0，得C₂=0。由此得到

这就是极值曲线的参数方程，它是一个摆线方程，常数C₁可以根据曲线必须通过点B这一条件确定。

一般说来，函数求极值得到的是一个数，而泛函变分得到的是一个函数或者微分方程加边界条件，应用欧拉方程还可求解各种较复杂泛函的变分问题。例如，求泛函

满足边界条件y（0）=0，y（1）=1的极值曲线。由

注意到变分运算中x作为常量，得

利用分部积分，上式中括弧内的第一项可进一步简化

代回原式，得

因_η（x₁）=η（x₂）=0，得2y′δy₀¹=0。从而

由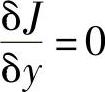，得

y″-6x=0

应用欧拉方程，会得到完全相同的结果。对上述微分方程积分两次，可得极值曲线为

y=x³+C₁x+C₂

最后将边界条件代入，得

C₁=C₂=0

于是得到所求极值曲线为

y=x³

当泛函的形式复杂时，这种直接求解的方法会遇到困难。