为了进一步理解泛函和变分的概念,下面对照函数的基本概念来介绍变分的基本概念。
1.函数定义与泛函定义
对函数来说,给定两个数集X和Y,x是X中的变量,y是Y中的变量。若存在一个对应关系,使x的每一个值都与y的某个值相对应,则称y是x函数,记为y=f(x)。X是函数的定义域,Y是函数的值域。
对泛函来说,给定满足一定条件的函数集合R1{y(x)}和实数集合R2,y(x)是R1中的变量,J是R2中的变量。若存在一个对应关系,使R1中每一个函数y(x)都有R2中的变量J与之相对应,则称变量J是y(x)的泛函,记为J=J[y(x)]。其中,y(x)是自变量,它是一个函数,J是因变量,它是一个实数。R1是泛函的定义域,R2是泛函的值域。由此可见,函数是因变量与自变量之间的关系,而泛函是因变量与函数之间的关系,可简单理解泛函是函数的函数,两种概念必须严格区分。还要指出,不能把复合函数与泛函混淆。在复合函数中,因变量是通过中间变量而依赖于自变量的,因变量与自变量之间有一一对应的关系。但在泛函中,因变量直接依赖于函数,与函数中的自变量没有对应关系,因给定一个自变量后,就有一个对应的函数,而由一个具体的函数值却不能给出一个泛函值。
2.函数的连续与泛函的连续
对函数y=y(x)来说,若对于自变量x的微小改变,有函数y(x)的微小改变与其对应,则函数y(x)连续。
对泛函J=J[y(x)]来说,若对于自变量y(x)的微小改变,有泛函J[y(x)]的微小改变与其对应,则泛函J[y(x)]连续。
可见,泛函的连续与函数的连续类似,但需要明确泛函的自变量,即函数y(x)的微小改变的含义。若有两条同类曲线y=y(x)和y1=y1(x),自变量的微小改变是指使y=y(x)和y1=y1(x)有定义的一切x值y(x)和y1(x)之差的模要很小,即曲线y=y(x)和另一条曲线y1=y1(x)的纵坐标之间很接近,如图2.1.3所示。有时不但纵坐标之间要接近,而且在对应点处的切线方向之间也要接近,即要求|y(x)-y1(x)|与|y′(x)-y1′(x)|都要很小,如图2.1.4所示。当|y(x)-y1(x)|很小时,称曲线y=y(x)和y1=y1(x)有零阶接近度,当|y(x)-y1(x)|与|y′(x)-y1′(x)|都很小时,称曲线y=y(x)和y1=y1(x)有一阶接近度,依此类推。
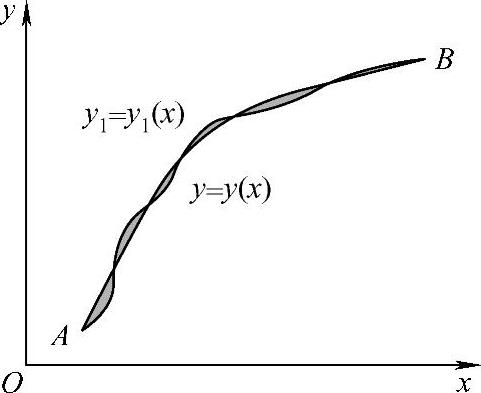
图2.1.3 零阶接近度
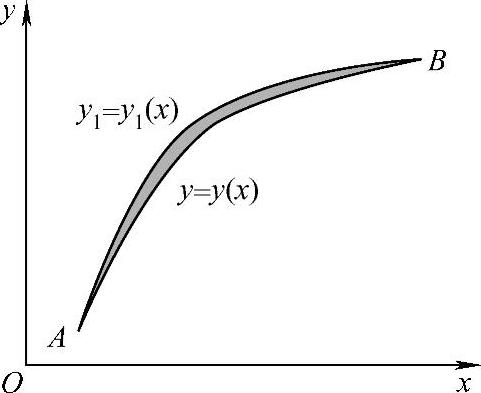
图2.1.4 一阶接近度
3.函数的微分与泛函的变分
先看函数的增量与泛函自变量的变分。对函数y=f(x)来说,自变量取增量Δx,相应地函数也有一增量Δy,即
Δy=f(x+Δx)-f(x)可见,函数的增量Δy是指同一条曲线y(x)上在x与x+Δx两点间的函数值之差。
对泛函J=J[y(x)]来说,自变量y(x)的增量是指y(x)与y1(x)两个函数值之差,并记为δy,即
δy=y(x)-y1(x)
当泛函的宗量y(x)有增量或变分Δy(x)=δy(x)时,则J[y(x)+δy(x)]-J[y(x)]就是泛函的增量,但泛函的增量,即使很小也不等于泛函的变分,这和函数的增量不等于函数的微分是一样的。
我们来讨论最简单的情况,例如,式(2.1.3)给出的泛函
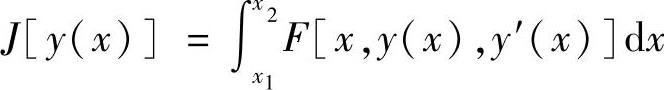
设想函数y(x)稍有变动,变为y+δy,则泛函的值也随之而变,变动的大小为

上式中,约等于号右端就是泛函J[y(x)]的变分,记作δJ[y(x)],即
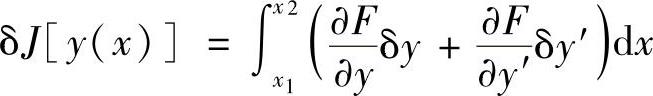
考虑泛函J(y,y′),其中,y=y(x)是泛函J在定义域R1中的函数。设η=η(x)是R1中的任一函数,ε是一个任意小的常量,泛函增量为
ΔJ=J(y+εη,y′+εη′)-J(y,y′)
显然可将J(y+εη,y′+εη′)对ε进行Taylor展开,即

于是
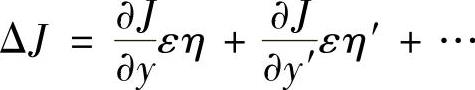
式中,省略号包含ε2,ε3,…等高阶小量项。该泛函增量表达式中的线性项就定义为泛函J的变分,记为
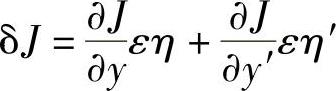
按照变分的这个定义,有
δy=εη,δy′=εη′
于是,得
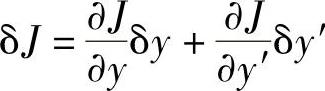
对于一般情形,若泛函
J=J[y1,y2,…,yn,y1′,y2′,…,yn′,…,y1(k),y2(k),…,yn(k)]
则变分表达式为
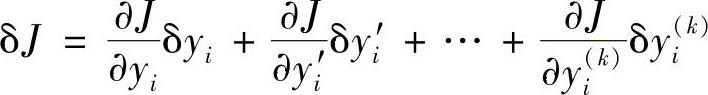
式中,下标i=1,2,…,n,且规定,若某项的下标重复时,就意味着它是n项求和,例如
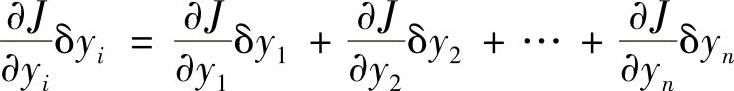
4.函数的极值与泛函的极值
对函数y=f(x)来说,如果函数f(x)在点x0的值f(x0)比它在点x0的适当小的邻域内各点的值都要大或都要小,即f(x0)>f(x)或f(x0)<f(x),则f(x0)就是函数f(x)的极大值或极小值。函数的极大值与极小值统称为函数的极值。
对泛函J=J[y(x)]来说,如果泛函J[y(x)]相应于某一条曲线y0(x)的值J[y0(x)]比相应于与y0(x)接近的任一条曲线的值都要大或都要小,即J[y0(x)]>J[y(x)]或J[y0(x)]<J[y(x)],则J[y0(x)]就是泛函J[y(x)]的极大值或极小值。同样,泛函的极大值与极小值统称为泛函的极值。
与函数求极值必须满足dy/dx=0的概念相似,取泛函J的极值时,也必须满足δJ/δy=0。为加深对极值的理解,我们引入拉格朗日(Lagrange)给出的微分定义。
定义 对函数y(x),若固定Δx,而ε为一小参变量,则函数的增量为
Δy=y(x+εΔx)-y(x)
函数的微分
 (https://www.daowen.com)
(https://www.daowen.com)
根据复合函数y(x+εΔx)的求导法则,有
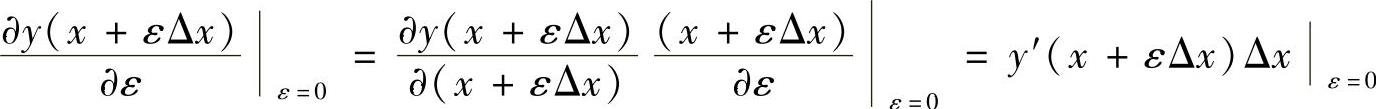
得
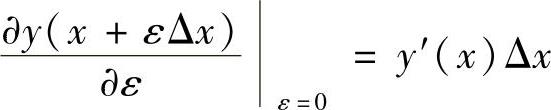
式中,因Δx为固定值,函数取极值,必有y′(x)=0,于是,得到函数取极值的条件为
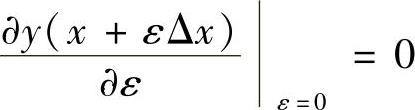
与此类似,变分命题就是泛函极值问题,为了便于说明,我们从最简单的固定端点问题的变分入手。如图2.1.5所示,首先找一任意光滑具有二阶导数的连续函数η(x),称其为比较函数,并使η(x)满足η(x1)=η(x2)=0。再取一参变量ε,它可在不太大的正负范围内变化,且令ε与x无关,以上限制主要保证泛函在极值处连续。设y(x)为待求的极值曲线,则有
y(ε,x)=y(x)+εη(x) (2.1.7)
为通过A和B两点的邻近于极值曲线的无限多条曲线。

图2.1.5 引入比较函数
由式(2.1.7),可得泛函J=J[y(x)]的增量为
ΔJ=J[y(x)+εη(x)]-J[y(x)]泛函的变分为
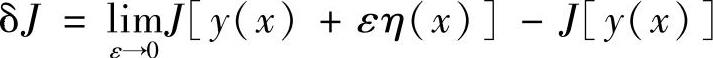
其中,函数的增量为
Δy=εη(x)
而函数的变分为
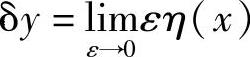
在研究泛函极值时,通常将η(x)固定,而令ε变化,这样规定的好处在于,建立由参数ε到泛函J[y(ε,x)]值之间的对应关系,这样泛函J[y(ε,x)]就成为参数ε的一般函数,或简写为J(ε),原泛函的极值问题就成为一般函数对ε的求极值的问题。与函数求极值时必须满足dy/dx=0的概念相似,为使泛函J取极值,必有

式(2.1.8)是下面将要导出的欧拉方程的理论基础。
应当指出,泛函极值有强极值与弱极值之分,因为曲线之间有不同的接近度。对零阶接近度而言,称作强极值,对一阶以上接近度而言,称作弱极值。下面我们通过对比来讨论变分运算与微分运算。
性质1 设有函数y(x),n为常量,则
dyn=nyn-1dy
δyn=nyn-1δy
性质2 设有函数u(x)和v(x),则
d(uv)=udv+vdu
δ(uv)=uδv+vδu
性质3 设有函数y(x),则
d(xy)=ydx+xdy
δ(xy)=xδy
性质3揭示了微分与变分之间的主要差别。由微分的定义可知,dy是由引起dx的,微分计算时突出了x是一个自变量,所以dx≠0,由变分的定义可知,δJ是由δy引起的,但δJ并不是由δx引起的。δy=y(ε,x)|ε→0-y(x)是在x为同一值时得到的。如图2.1.5所示,δy是定义在x为固定值的一条竖直线上,所以δx=0,即变分计算时突出了x是一个常量。
性质4 由y(ε,x)=y(x)+εη(x),对x求偏导数,得
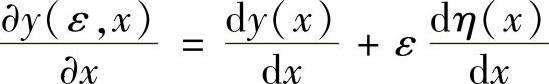
或写为y′(ε,x)=y′(x)+εη′(x)
而
δ(y′)=y′(ε,x)ε=0-y′(x)=εη′(x)ε=0(2.1.9)
由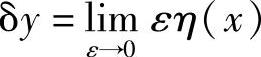 ,对x求导数,得
,对x求导数,得

比较式(2.1.9)和式(2.1.10),可得
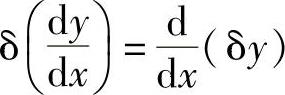
或
δ(y′)=(δy)′(2.1.11)
式(2.1.11)表明,微分和变分的次序可以交换。
此外,还有

以及
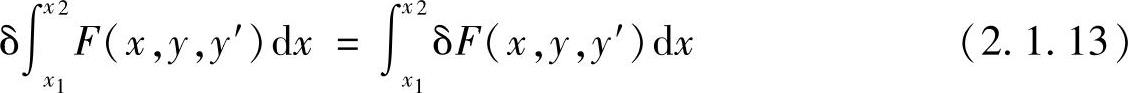
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





