我们熟知函数y=y（x），因变量的值通过自变量x来确定。在实际工程问题中，会遇到一种特殊类型的函数，这时因变量的值需由一个函数或几个函数确定。例如，求连接xOy平面上两个给定点A（x₀，y₀）和点B（x₁，y₁）之间的曲线长度J，由图2.1.1可知，由于长度J是由连接A和B两点间的曲线形状所决定的，曲线形状不同，长度就不同，所以长度J是由曲线方程y=y（x）确定的。虽然作为几何学的公理，两点间距离以直线为最短，但我们还是希望从变分法的角度对这个公理作出论证。由高等数学可知

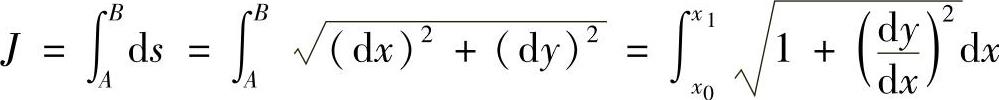
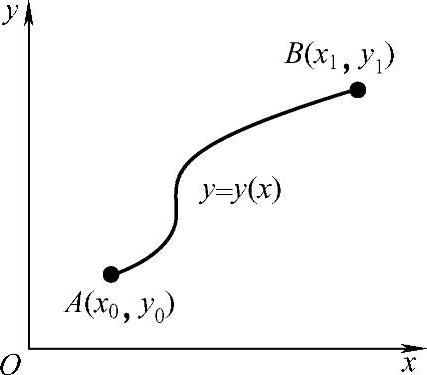
图2.1.1 曲线长度

可见，只要给出具体的曲线方程，就可由上式算出曲线长度，而不同的曲线方程对应着不同的长度，因此，曲线长度J是曲线y=y（x）的函数。这种函数值由一个或几个函数所确定的函数，称为泛函。本例中，曲线长度J是曲线y=y（x）的泛函，并记作J[y（x）]，即

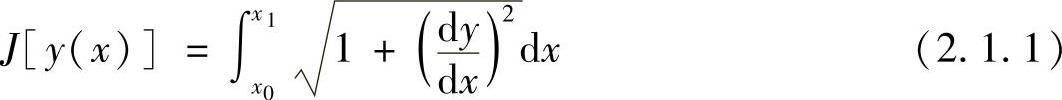
我们知道，函数有极值问题，由函数的极值会想到泛函的极值。例如，在上例中，由于xOy平面上两个给定点间的曲线长度J是曲线y=y（x）的泛函，所以如果要确定长度最短的曲线方程y=y（x），就是求泛函J[y（x）]的极小值问题。研究函数的极值问题采用微分法，而研究泛函极值的方法就是变分法，泛函极值问题就是变分命题，变分计算的目的就是把极值曲线y（x）找出来。

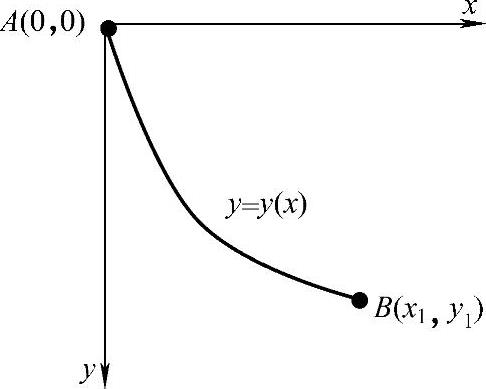
图2.1.2 最速下降线问题

下面介绍一个数学史上著名的变分命题——最速下降线问题。如图2.1.2所示，设点A（0，0）和点B（x₁，y₁）在不同的竖直线上，现用某一曲线y=y（x）连接A和B两点，使质量为m的重物沿此曲线无摩擦地自由下滑。显然，曲线y=y（x）的形状不同，由点A自由下滑到点B所需要的时间也不同，试问沿哪一条曲线下滑所需时间t最少？

根据机械能守恒定律，若重物从点A下滑到任一点（x，y）时速度为u，从点A到该点失去的势能为mgy，获得的动能为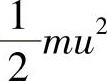，所以由机械能守恒定律，有

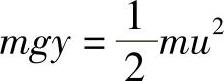
式中，g为重力加速度。于是，得到点（x，y）的速度为

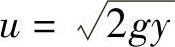
而

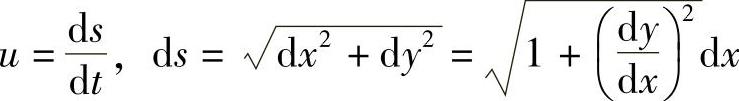
于是有

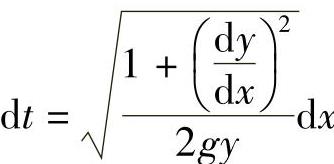
则从A到B自由下滑所需的时间为

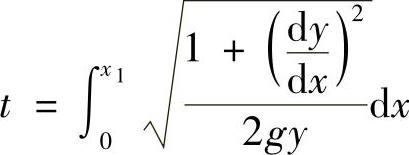(www.daowen.com)

可见，重物下滑时间是函数y=y（x）的泛函，并记为J[y（x）]，即

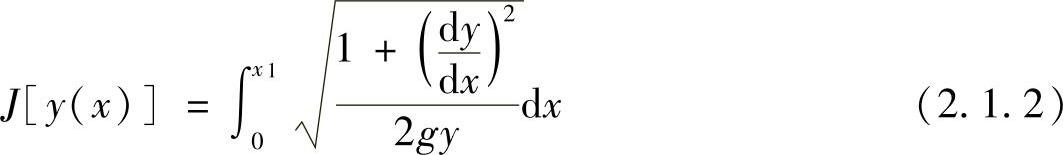
对于不同的函数y（x），对应着不同的时间，而最速下降线问题就是求时间t最小时的函数y（x）。这个变分命题可表述为，在满足y（0）=0，y（x₁）=y₁的一切y=y（x）函数中，选取一个函数，使式（2.1.2）的泛函J[y（x）]为最小值。由这个经典变分命题我们可以发现，自变量只有一个x，待定函数也只有一个y（x），函数的导数只有一阶，而且边界是固定的，即自变量的端点与函数的端点值都是固定不变的。因此，最速下降线变分命题是一个泛函，包括一阶导数、具有一个待定函数、含有一个自变量、端点固定的无条件变分命题。这是变分法中一种最简单的变分命题，这个最简单的变分命题可写成一般形式，即

在通过y₁=y（x₁），y₂=y（x₂）两个端点的情况下，选取y（x），使泛函

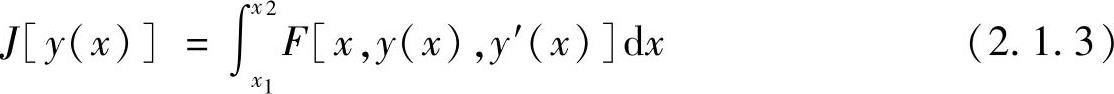
有极值。

对于泛函含有高阶导数，例如，包含y′（x），y″（x），…，y（n）（x）的变分命题，其泛函形式为

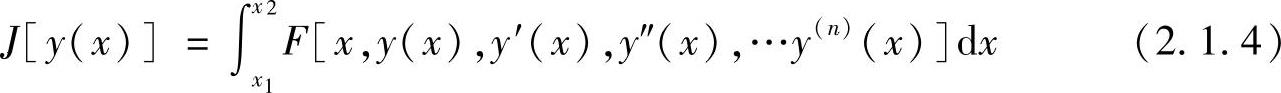
其相应的边界条件为

y（x₁）=y₁，y′（x₁）=y′₁，…，y^（n-1）（x₁）=y₁^（n-1）

y（x₂）=y₂，y′（x₂）=y′₂，…，y^（n-1）（x₂）=y₂^（n-1）

对于泛函具有多个待定函数，例如，包含两个待定函数y（x），z（x）的变分命题，其泛函形式为

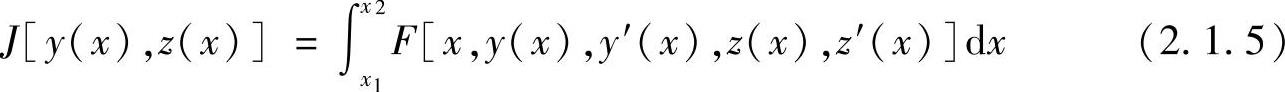
其相应的边界条件为

y₁=y（x₁），y₂=y（x₂），z₁=z（x₁），z₂=z（x₂）

对于泛函含有多个自变量，例如，包含两个自变量x，y的变分命题，其泛函形式为

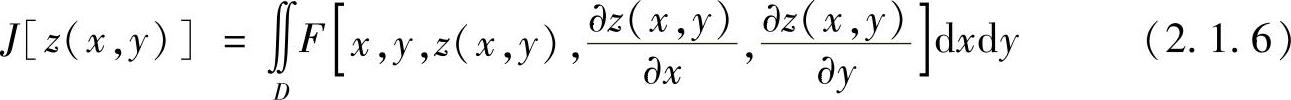
其相应的边界条件为函数z（x，y）在计算域D的边界Γ上的值已给定。