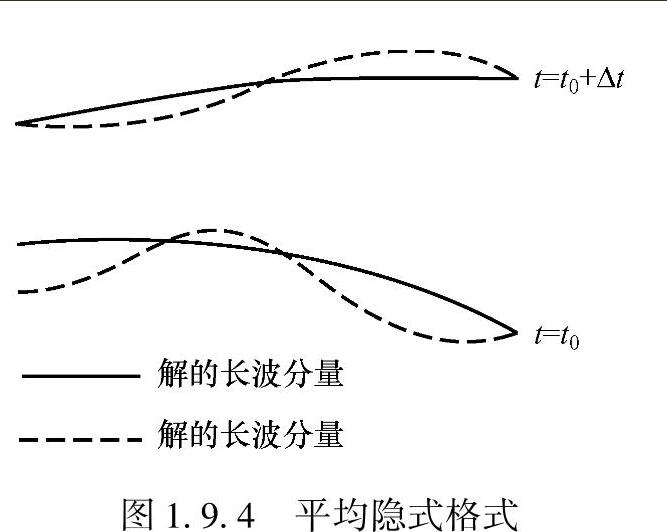
【摘要】：下面的分析表明，大的Δt对平均隐式格式会产生解的短波分量的空间振荡和摆动，即数值振荡。同时，对于长波分量来说，kΔx→0，则有sinkΔx→0，于是放大因子r→1，每推进一时间步长Δt，长波分量的相位改变很少，如图1.9.4所示。因为Δt很大时，r→0，解会由于大的数值耗散而不断衰减，短波分量也被衰减了，所以不会出现振荡。
全隐和平均隐式格式都是恒稳的，可取较大的时间步长Δt，由于存在数值耗散，当Δt过大时会影响计算精度，因此，时间步长Δt需根据具体问题以及计算精度的要求确定。
下面的分析表明，大的Δt对平均隐式格式会产生解的短波分量的空间振荡和摆动，即数值振荡。一维对流方程的六点格式（CrankNicolson，CN格式）的放大因子为
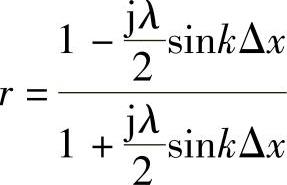
其模|rh|=1，格式恒稳，计算幅值无衰减，数值耗散系数为零。
若把时间步长Δt取得很大，从而λ＞＞1。对于短波，波长λω≅4Δx，kΔt≅1，则sinkΔx≅1，于是
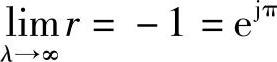
这时放大系数的辐角Δφ→π，说明经过Δt时间后同一x位置的短波分量相位改变了180°，短波分量产生了振荡。同时，对于长波分量来说，kΔx→0，则有sinkΔx→0，于是放大因子r→1，每推进一时间步长Δt，长波分量的相位改变很少，如图1.9.4所示。这样，当取大的时间步长时，平均隐式格式引起了短波分量的数值振荡，使计算不稳定。
利用CN格式求解一维扩散方程时，其放大因子为(www.daowen.com)
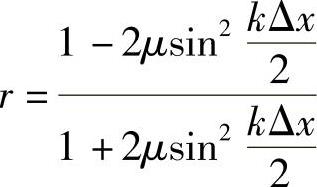
式中，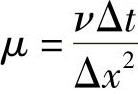
。
对于短波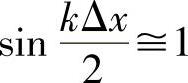
，
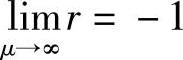，产生数值振荡。因为
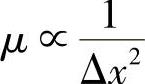，若取同样的Δt和Δx时，扩散方程的CN格式比对流方程的CN格式更容易产生振荡。
无论对流方程还是扩散方程，其全隐格式都不产生数值振荡。因为Δt很大时，r→0，解会由于大的数值耗散而不断衰减，短波分量也被衰减了，所以不会出现振荡。全隐格式的另一个特点是波相速度减小。
的短波数值振荡
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
