› 理论教育 ›数值耗散和弥散—偏微分方程数值解法

数值耗散和弥散—偏微分方程数值解法

时间：2023-10-26 理论教育 版权反馈
【摘要】：用差分方程逼近微分方程时引入了误差，有时这些误差项使计算结果的幅值衰减，且相速度发生变化，其作用相当于流动中的物理耗散和弥散，这种虚假的物理效应称做数值耗散和弥散。用放大因子泰勒展开求得的数值耗散和弥散系数和前面将差分方程直接展开得到的结果是完全一致的。图1.9.2 全隐格式的数值耗散图1.9.3 全隐格式的数值弥散图1.9.3上给出了λ=1时，数值解相位滞后角Δφh与精确解相位滞后角Δφ之比随kΔx的变化关系。

数值耗散和弥散—偏微分方程数值解法

用差分方程逼近微分方程时引入了误差，有时这些误差项使计算结果的幅值衰减，且相速度发生变化，其作用相当于流动中的物理耗散和弥散，这种虚假的物理效应称做数值耗散和弥散。

一维波动方程式（1.9.1）描述了既无耗散又无弥散的流体运动，下面我们讨论用全隐格式逼近它时，产生的数值耗散和弥散。一维对流方程式（1.9.1）的全隐格式是

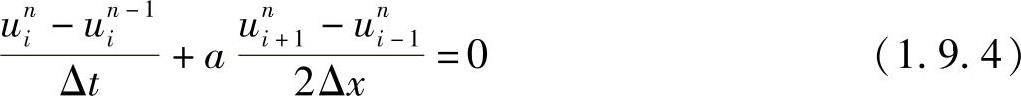
978-7-111-44528-9-Chapter01-369.jpg

作以下泰勒级数展开，有

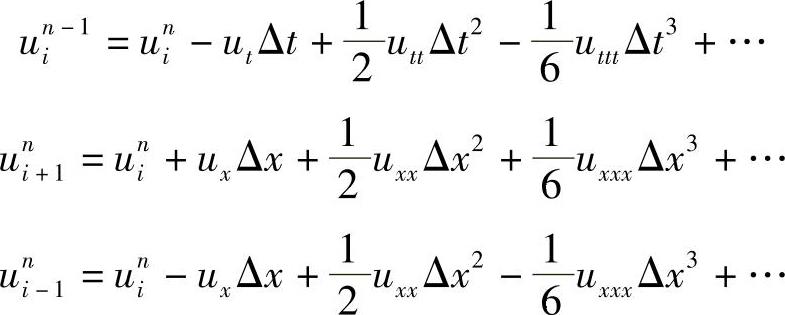
978-7-111-44528-9-Chapter01-370.jpg

把三个展开式代入式（1.9.4）并整理，得

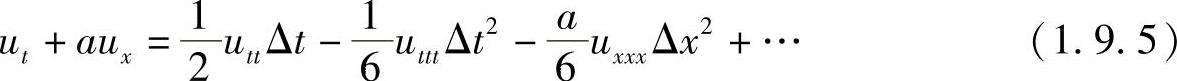
978-7-111-44528-9-Chapter01-371.jpg

这是全隐格式所逼近的精确的微分方程。现在设法把它右边对时间t的导数项转换成对空间x的导数，来讨论数值耗散和弥散.为此，先将方程式（1.9.5）写成

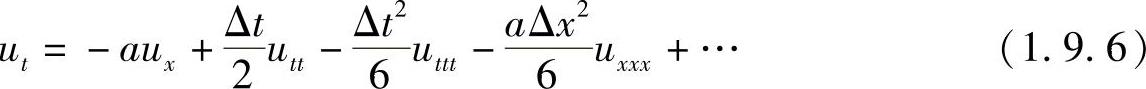
978-7-111-44528-9-Chapter01-372.jpg

上式对t微分一次，得

978-7-111-44528-9-Chapter01-373.jpg

将式（1.9.6）代入式（1.9.7），得

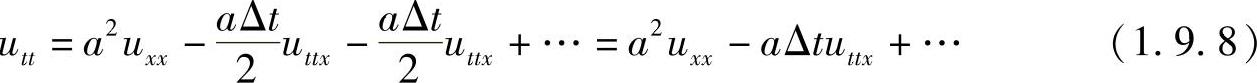
978-7-111-44528-9-Chapter01-374.jpg

上式对x求一阶导数一次，得

uttx=a2uxxx+…

将此式代入到式（1.9.8），得

utt=a2uxx-a3Δtuxxx+… （1.9.9）

将式（1.9.9）等式两端同时对t微分，得

uttt=a2（ut）xx+…

再次把式（1.9.6）代入上式，得

uttt=-a3uxxx+… （1.9.10）

这样，式（1.9.9）和式（1.9.10）分别把对时间的二、三阶导数用对空间的导数表示出来，将此二式代入方程式（1.9.5），得到

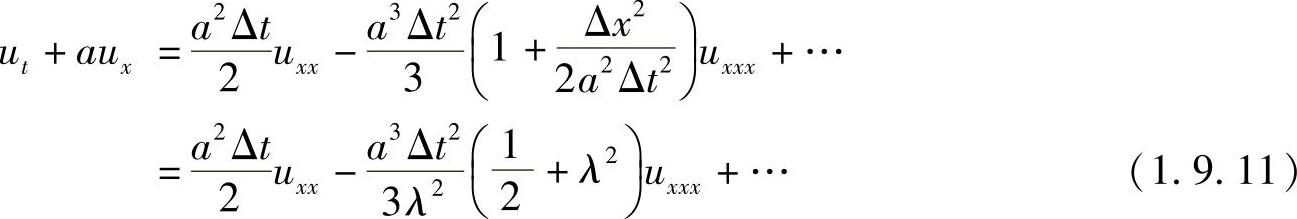
978-7-111-44528-9-Chapter01-375.jpg

式中，λ=aΔt/Δx。

在以上推导过程中写出了三阶导数，高阶项用省略号表示。这样方程式（1.9.11）是差分方程精确表达的微分方程。当忽略了全部截断误差后，它才是一维对流方程。换言之，差分方程式（1.9.4）精确表达微分方程式（1.9.11），忽略截断误差后，它才近似逼近对流方程式（1.9.4）。

将式（1.9.11）与有耗散方程式（1.9.2）和有弥散的方程式（1.9.3）比较，可知其对空间二阶导数项有耗散作用，而三阶导数项起弥散作用。因此，得到二阶数值耗散系数为

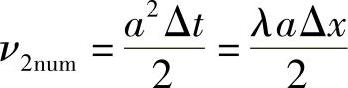
978-7-111-44528-9-Chapter01-376.jpg

三阶数值弥散系数为

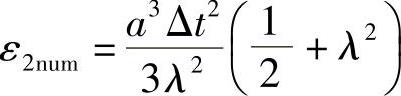
978-7-111-44528-9-Chapter01-377.jpg

全隐格式（1.9.4）引进了对流方程式（1.9.1）所没有的耗散和弥散项，计算将产生阻尼误差和相位误差，是虚假的物理效应。当Δx与Δt取得很小时，数值耗散和弥散系数就很小，计算误差就小。虽然全隐格式恒稳，可取较大的步长，但仍然受到精度的限制。

由方程式（1.9.11）可得到全隐格式的第一微分近似方程

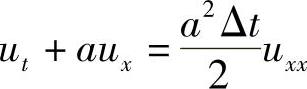
978-7-111-44528-9-Chapter01-378.jpg

从判别稳定性的Hirt启示法可知，因为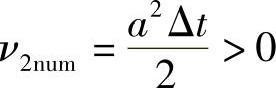978-7-111-44528-9-Chapter01-379.jpg，所以全隐格式是稳定的。这样Hirt直接稳定性判别法可叙述为，如果格式的数值耗散系数ν2num＞0，则格式稳定，反之，若ν2num＜0，则格式不稳定。可见，这是一个非常简便而直观的判别稳定性的必要条件。

采用稳定性的傅里叶分析方法可得全隐格式的放大因子rh为

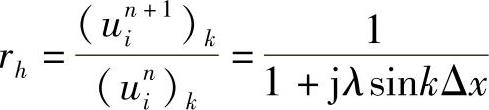
978-7-111-44528-9-Chapter01-380.jpg

放大因子的模

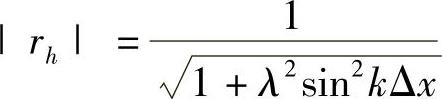978-7-111-44528-9-Chapter01-381.jpg(www.daowen.com)

辐角为

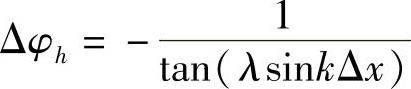
978-7-111-44528-9-Chapter01-382.jpg

相速度为

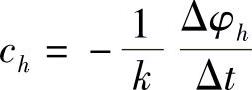
978-7-111-44528-9-Chapter01-383.jpg

考虑长波分量，λω＞＞1，kΔx＜＜1，将放大因子的模作泰勒级数展开，有

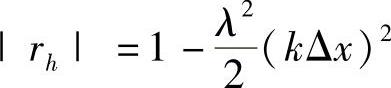
978-7-111-44528-9-Chapter01-384.jpg

把二阶物理耗散波动方程的精确解的放大系数的模，同样作泰勒级数展开，有

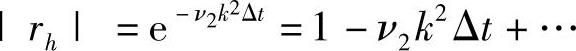
978-7-111-44528-9-Chapter01-385.jpg

比较以上两个展开式的第二项，可知全隐格式引进的耗散与波动程式（1.9.1）的二阶耗散是等价的。所以有

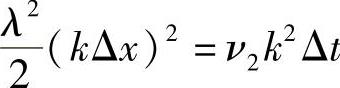
978-7-111-44528-9-Chapter01-386.jpg

此可得全隐格式的数值耗散系数

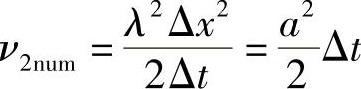
978-7-111-44528-9-Chapter01-387.jpg

类似地，把差分方程的放大因子的辐角作泰勒展开，得

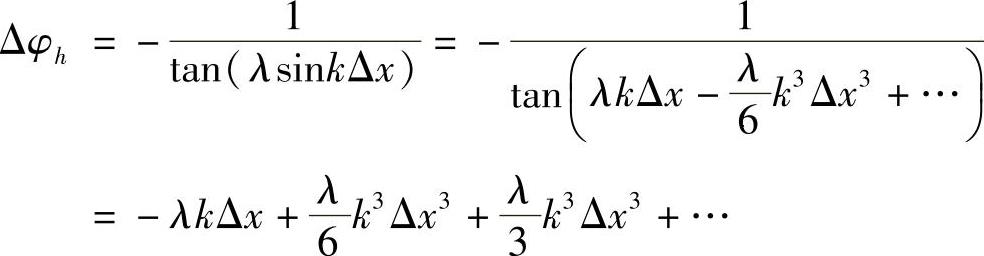
978-7-111-44528-9-Chapter01-388.jpg

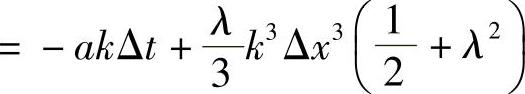
978-7-111-44528-9-Chapter01-389.jpg

相速度的展开为

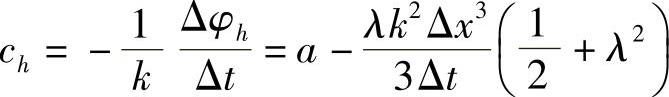
978-7-111-44528-9-Chapter01-390.jpg

全隐格式引进的弥散作用等价于有三阶弥散系数的波动方程的弥散作用。比较式（1.9.11）和式（1.9.3）的放大系数的辐角，易得

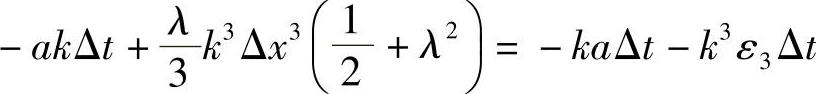
978-7-111-44528-9-Chapter01-391.jpg

即

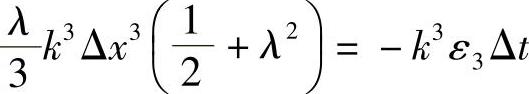
978-7-111-44528-9-Chapter01-392.jpg

所以得到数值弥散系数

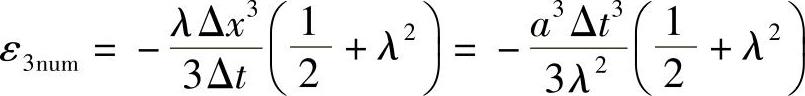
978-7-111-44528-9-Chapter01-393.jpg

同样，比较全隐格式相速度展开式（1.9.12）与式（1.9.3）的相速度，也可得到数值弥散系数。用放大因子泰勒展开求得的数值耗散和弥散系数和前面将差分方程直接展开得到的结果是完全一致的。因此，从格式放大因子就可以直接分析格式的数值效应。

放大系数的模如图1.9.2所示。从图中可以看出|rh|≤1，全隐格式是恒稳的。当kΔx=0和kΔx=π时，|rh|=1，格式无衰减。这分别相应于λω＞＞Δx和λω=2Δx，前者是极长波，而后者是不辨认的短波。当kΔx=π/2时，衰减最大，|rh|=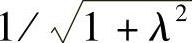978-7-111-44528-9-Chapter01-394.jpg，此时波长λω=4Δx。由分析可知，格式对于长波分量是好的近似，而对于短波则是不好的近似。从图1.9.2还可看出，虽然全隐格式是恒稳的，但λ大时计算误差也大，为保证精度，一般取λ为1左右。

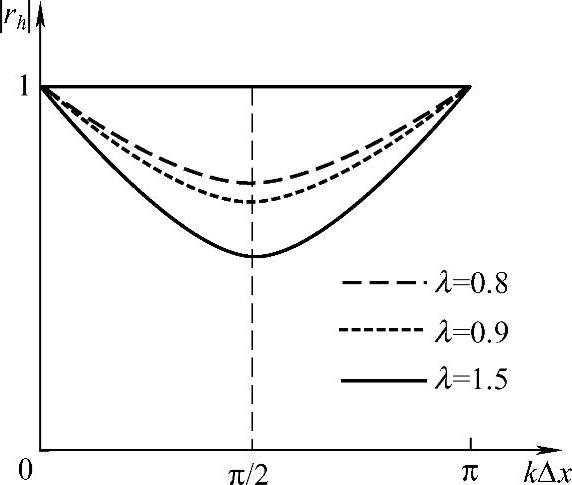
978-7-111-44528-9-Chapter01-395.jpg

图1.9.2 全隐格式的数值耗散

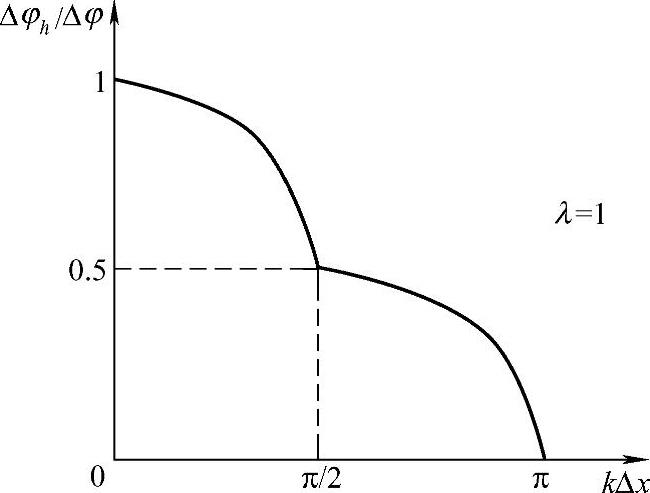
978-7-111-44528-9-Chapter01-396.jpg

图1.9.3 全隐格式的数值弥散

图1.9.3上给出了λ=1时，数值解相位滞后角Δφh与精确解相位滞后角Δφ之比随kΔx的变化关系。当kΔx从0变到π时，相位弥散不断增加，因此，仍然可得出格式对长波是好的近似，对短波是不好的近似。

若用数值格式计算有物理耗散的方程

ut+aux=νuxx

则差分方程会带来数值耗散和弥散效应。若数值耗散大于物理耗散，即νnum＞ν，则数值效应掩盖了物理本质，计算的结果将失去物理意义。因此，选用差分格式时必须满足νnum＜ν。对前面分析的全隐格式来说，若计算中取λ=aΔt/Δx=1，则要求

νnum=aλΔx/2=aΔx/2＜ν

格式的耗散效应能起到光滑解和消除计算中偶然误差的作用。因此，可以利用适当的数值耗散来抑制不希望的数值振荡，加强格式的稳定性和求解有间断性的流动。但过大的长波衰减会降低计算精度，所以有时希望格式的νnum既不太大，又不为零。

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。

我要反馈

有关偏微分方程数值解法：土建类的文章