首先讨论一维行波的性质，波高可写为

ζ（x，t）=Ae^jk（x-ct）

其中，c表示单位时间波传播的距离，称为相速度，且有c=λωf，f为频率。定义相函数φ=k（x-ct），沿着φ=const的直线，波高处处相等，于是得到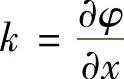，即波数是相函数的空间导数。而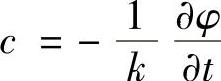，即相速度是相函数的时间导数与空间导数之比。

物理耗散现象是指波幅A因阻尼作用而衰减的现象，而弥散现象是指波的相速度c随波数发生变化的现象。例如，深水波的相速度为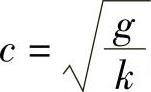。长波λω大，波数k小，相速度c就大，传播快。反之，短波的相速度小，传播慢，这种波就称为弥散波，或称色散波。例如，浅水波的相速度为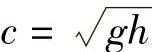（h为平均水面的高度），相速与波数无关，称为非弥散波。为了弄清数值耗散和色散效应的本质，下面以三个模型方程为例，讨论物理耗散与弥散现象。

1.无耗散和弥散的模型

u_t+au_x=0 （1.9.1）

设方程的解可由傅里叶级数表示为

则波数为k的波分量可写为

u_k=A_kejk（x-at）

这一波分量是满足对流方程的，考虑经过了Δt时间后，其解可写成

u_k（x，t+Δt）=A_ke^{jk[x-a（t+Δt）]}

定义放大因子

放大因子的模|r|=1，说明波在传播过程中，经过Δt时间波幅值没有衰减。放大因子的辐角Δφ=-kaΔt，表明传播了Δt时间后，同一位置处波的相位迟后为Δφ。它是相函数的差，即Δφ=φ（x，t+Δt）-φ（x，t）。而相速度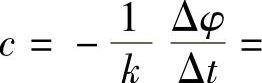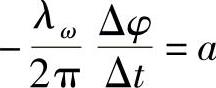，相速度与波数无关，没有色散现象。故对流方程式（1.9.1）描述了无衰减，无弥散的物理现象。

2.有耗散的模型

u_t+au_x=ν₂u_xx+ν₄u_x^（4） （1.9.2）

中ν₂与ν₄分别称为二阶和四阶耗散系数。利用参数变易法，令解的一个波分量为

u_k=A_k（t）e^jk（x-at）

把波分量解代入方程式（1.9.2），可得

于是，得

由此可知相速度c=a为常数，但幅值A_k（t）随时间而衰减。方程式（1.9.2）描述了有物理耗散而无色散的波运动。

若只考虑二阶耗散系数，则波分量为

经过Δt时刻后，有

放大系数为

放大系数的模

放大系数的辐角

Δφ=-kaΔt(www.daowen.com)

相速度

可见，有二阶耗散的方程描述了有物理耗散的波动，耗散系数引起波幅的衰减，但相速度不发生改变，放大系数辐角也与方程式（1.9.1）的相同。

3.有弥散的模型

u_t+au_x=ε₃u_x^（3）+ε₅u_x^（5） （1.9.3）

中ε₃与ε₅分别称为三阶和五阶弥散系数，可取正或负值。

令

u_k=A_k（t）e^jk（x-at）

代入方程式（1.9.3），可得

于是，得

波分量的幅值不随时间变化，而相速度c=a+ε₃k²-ε₅k⁴是波数k的函数。方程式（1.9.3）描述了有弥散的波动。

若只考虑三阶色散，则解分量可写成

经过Δt时刻后，有

放大系数为

放大系数的模

|r|=1

放大系数的辐角

Δφ=-kaΔt-k³ε₃Δt

相速度

可见，三阶色散作用下波幅没有衰减，但相速度是波数的函数，当ε₃＞0时，相速度增加，波传播加快。与前两种模型相比，放大系数的辐角也增加了一项，这说明在同一位置x，经过Δt时间后的相位滞后比无色散的波要大。

定义总动能

定义总动量

假定|x|→∞时，u，u_x，u_xx，…分别趋于零，考虑上面三种模型方程动能和动量的守恒关系。

积分方程式（1.9.1），得

故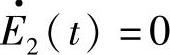。将方程式（1.9.1）的两端同乘以u，然后积分，可得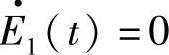。可见，无耗散和色散的运动，其动能和动量是守恒的。同样，仅有弥散时波动的动能和动量也是守恒的。对有耗散的方程式（1.9.2），经过同样的推导可得

这表明有耗散作用时总动量守恒，而总动能是不断衰减的。