对流扩散方程是一类基本的运动方程，其对于对流扩散问题数值计算方法的研究具有重要的理论和实际意义，因此，对流扩散问题的数值解法一直是计算数学中重要的研究内容。我们在前面已经简单介绍了一维线性对流扩散方程式（1.1.16）

并且也已讨论了对流方程和扩散方程的差分方法，实际上，将两者结合起来就可得求解对流扩散方程的差分方法。

1.中心显式差分格式

将时间导数用前差格式，空间导数用中心差分格式，得

显然，中心显式差分格式（1.8.15）的截断误差为O（τ+l²）。若β=0，则式（1.8.15）就是对流方程的差分格式。应用稳定性的Fourier分析方法可得中心显式差分格式的稳定性条件为

式（1.8.17）是扩散方程向前差格式的稳定性条件，由于增加了对流项，因此对时间步长τ也增加了限制条件式（1.8.16）。

2.迎风差分格式(www.daowen.com)

由中心显式差分格式的稳定性条件式（1.8.14）可得，当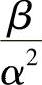的值较小时，时间步长一定会很小，为克服这个不利因素，在一阶空间偏导数的离散中采用单边差商，若α＞0，则

迎风格式就是在中心显式格式中把对流项的中心差商换成由α的符号所确定的单边差商。显然，迎风格式的截断误差为O（τ+l）。迎风格式的稳定性条件为

迎风格式虽然是一阶精度的差分格式，但在实际计算中还是经常采用的。特别是在对流项系数比扩散项系数大很多的情况下，即所谓对流占优的问题，采用中心显式格式已不能计算出问题结果，而用迎风格式仍可计算出问题的近似解。

3.隐式差分格式

前面讨论的显式格式都是有条件稳定的，为了放宽稳定性要求，可以采用隐式格式进行求解。可以利用上面的显式差分格式构建隐式差分格式。从中心显式格式出发，可构建六点格式

隐式差分格式（1.8.20）无条件稳定。