对于二维扩散方程的初边值问题

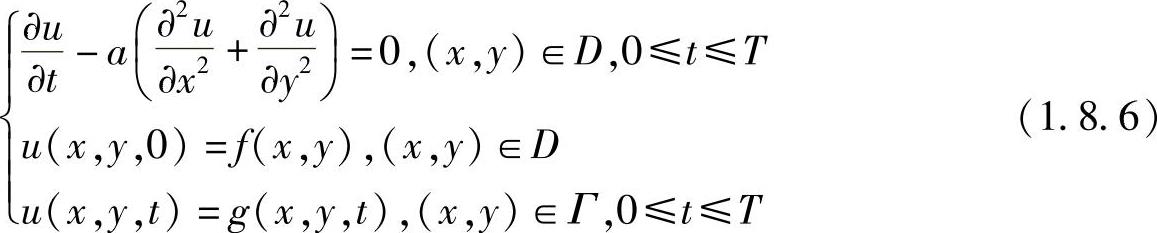
为讨论问题方便，设边界为Γ的计算域D是矩形域0≤x≤b，0≤y≤c。

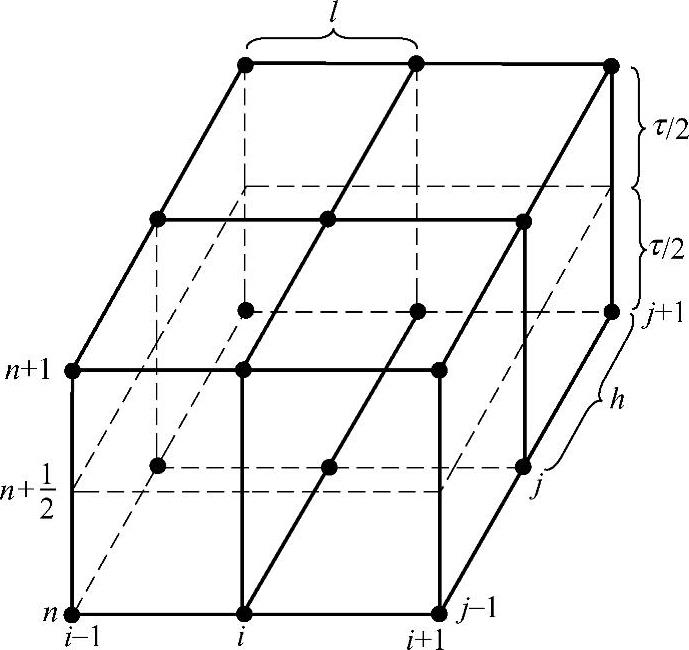
图1.8.6 二维扩散方程差分网格

采用显式格式，如图1.8.6所示，写出二维扩散方程式（1.8.6）的差分格式

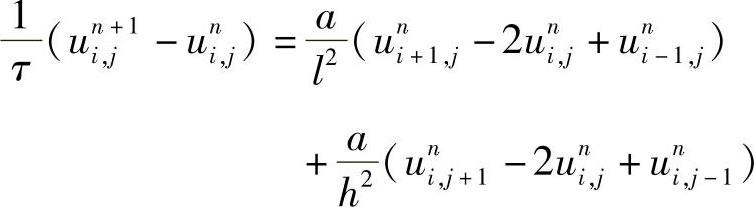
令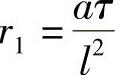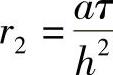，，上式可改写为

uⁿ_i，j⁺¹=r₁uⁿ_i+1，j+r₁uⁿ_i-1，j+r₂uⁿ_i，j+1+r₂uⁿ_i，j-1+（1-2r₁-2r₂）uⁿ_i，j （1.8.7）

式（1.8.7）的稳定性条件为

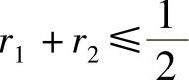
若取l=h，r=r₁=r₂，则差分方程式（1.8.7）可以写成

uⁿ_i，j⁺¹=r（uⁿ_i+1，j+uⁿ_i-1，j+uⁿ_i，j+1+uⁿ_i，j-1）+（1-4r）uⁿ_i，j （1.8.8）

而这时的稳定性条件为

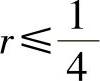
用上述显式格式求解二维扩散方程问题，由于稳定性条件较苛刻，计算工作量大，一般较少采用。如采用隐式格式，写出二维扩散方程（1.8.6）的差分格式

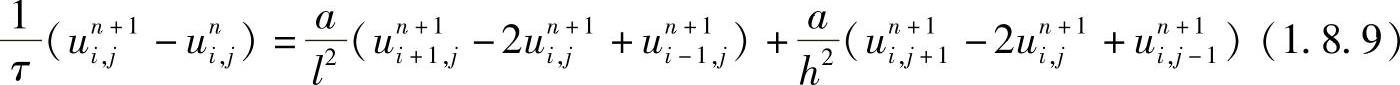
虽然式（1.8.9）是无条件稳定的，但在每一个时间层上需要解一个五对角的代数方程组，求解并不方便。而若采用类似于六点格式的隐格式，其求解也是不方便的，为此需要建立新的差分格式，希望这个差分格式无条件稳定，有合理的精度，且所构建的代数方程易于求解。下面简要介绍交替方向隐式格式（Alternating Direction Implicit，ADI），这种方法的基本思想是将二维的问题逐次化为关于x，y方向的两个一维问题，再应用追赶法求解。具有代表性的交替方向的隐式方法是PeacemanRachford方法，其差分格式是无条件稳定的。PeacemanRachford方法，对相邻两个时间层交替使用两个差分方程

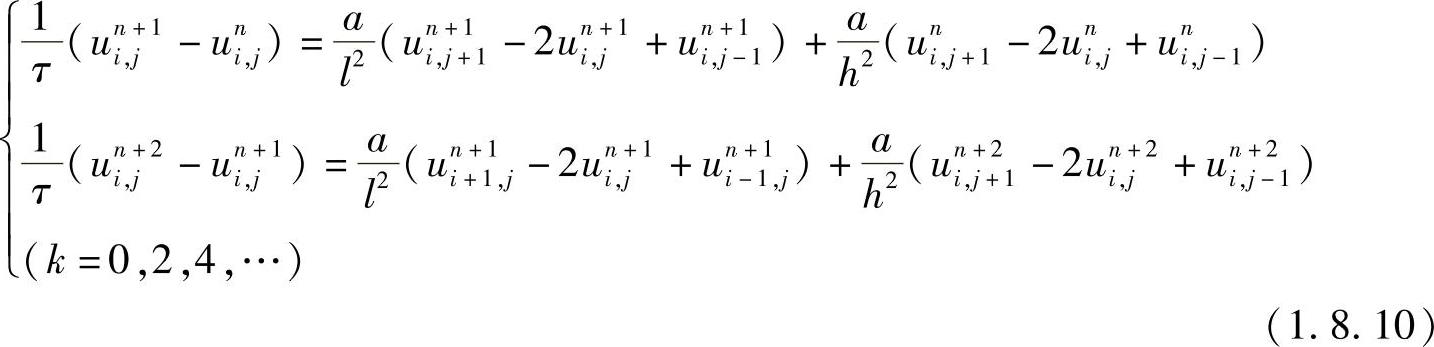(www.daowen.com)

其中，前一个方程组只对x方向进行求解，后一个方程组只对y方向进行求解。在每一个时间层所要解的方程组都是三对角的，可用追赶法求解。建立这个差分格式的出发点是为了克服隐式格式的缺点。在某一时间层上，将二阶导数之一，例如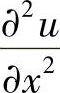，取成隐式，即用u的未知值的二阶中心差商代替，而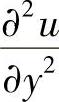取成显式，即用u的已知值的二阶中心差商代替，这样得到的方程组仅在x方向是隐式的，容易求解。对于下一个时间层，将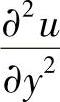取成隐式，而将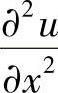取成显式，重复这一做法。这样相继的两个时间层合并所构成的差分格式，对任何时间步长都是稳定的。

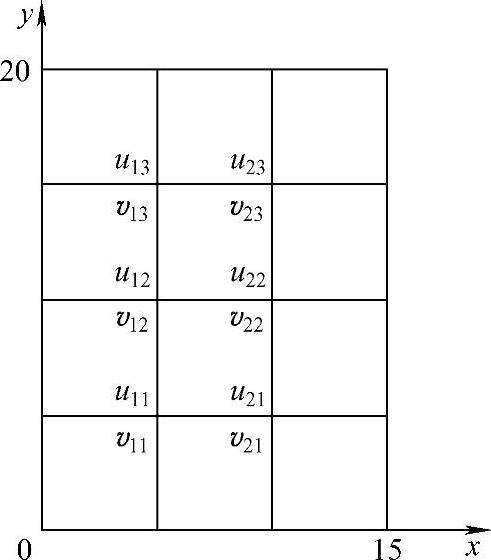
图1.8.7 xOy平面上的二维扩散方程差分网格

考虑二维非稳态热传导定解问题

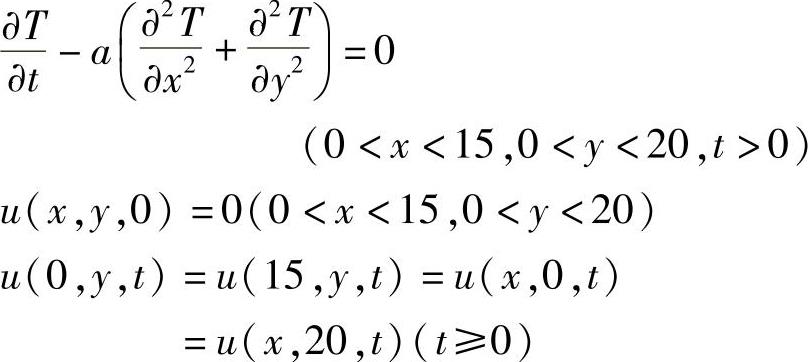
在xOy平面上作正方形网格，如图1.8.7所示，二维扩散方程差分网格空间步长取l=5，时间步长取τ=2.5，得

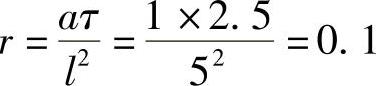
于是，可根据式（1.8.10）写出泛定方程的边界条件与网格法差分格式为

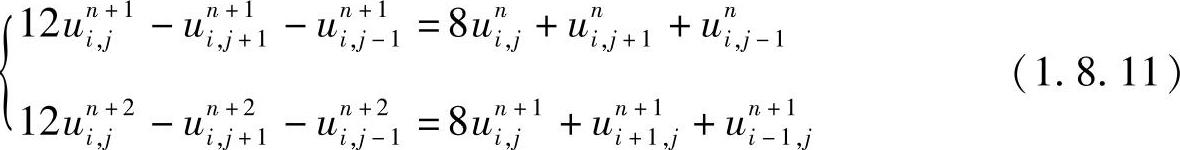
注意到式（1.8.10）是针对内点而言，由于本定解问题是第一类边界条件，边界的值可以直接转移，因此，在x方向上内点的编号为i=1，2，在y方向上内点的编号为j=1，2，3，我们需要求解6个未知量。因为n=0时刻的初始值为已知，即式（1.8.11）中的第一个等式的右端为已知，可以列出由6个方程组成的方程组，由此就可以求出n=1时刻的6个未知量，再以这6个未知量作为中间过渡值，代入到式（1.8.11）中的第二个等式的右端，即可得到n=2时刻的6个未知量，以此类推就可求出不同时刻结点上的温度值。为叙述方便，如图1.8.7所示，把过渡值uⁿ_i，j⁺¹用u₁₁，u₁₂，u₁₃，u₂₁，u₂₂和u₂₃表示，而把uⁿ_i，j⁺²用v₁₁，v₁₂，v₁₃，v₂₁，v₂₂和v₂₃表示，于是，差分方程组写成下列两个线性代数方程组

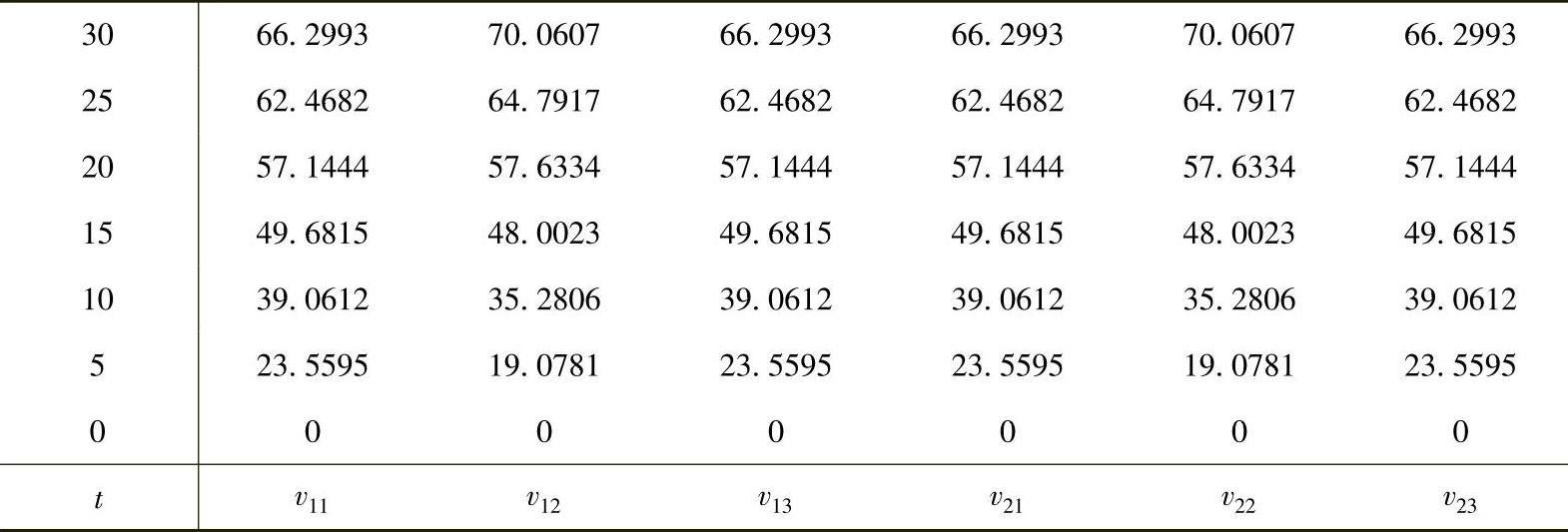
对式（1.8.12）和式（1.8.13）循环求解，就可得到不同时间层的v₁₁，v₁₂，v₁₃，v₂₁，v₂₂和v₂₃，计算结果如表1.8.1。

表1.8.1 定解问题计算结果

应当指出，PeacemanRachford方法格式不能推广到三维，而下面介绍的DouglasRachford方法可用于三维问题求解。这种方法在第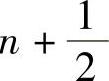层上取过渡层，通过过渡层计算n+1层，计算的两个差分方程为

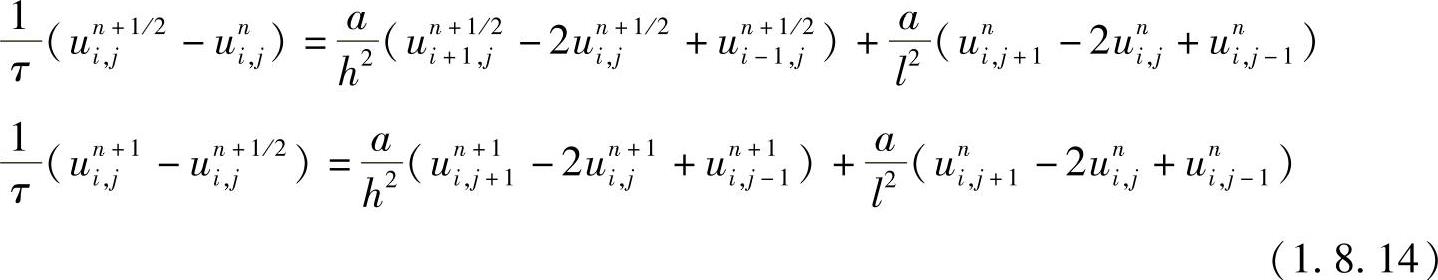
应用交替方向隐式方法求解抛物型方程时，除了可保证无条件稳定和合理的精确度之外，其所产生的代数方程组还便于求解。