现在讨论波动方程

为了分析简单或写成

的差分格式。

1.显式格式

空间和时间均采用中心差分格式

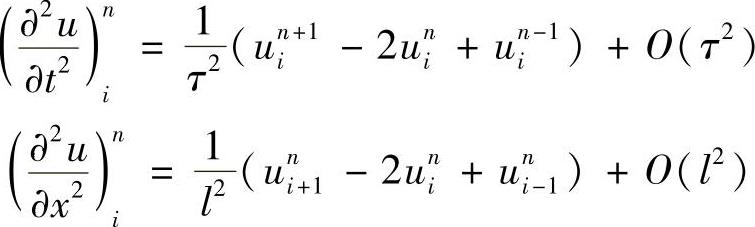
略去截断误差O（τ²+h²），得差分方程为

uⁿ_i⁺¹=r²（uⁿ_i+1+uⁿ_i-1）+2（1-r²）uⁿ_i-uⁿ_i-1-r²l²fⁿ_i （1.7.6）

式中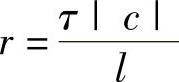，；f_jⁿ=f（x_j，t_n）。这是三层的显式格式，如图1.7.3所示。

应用稳定性的Fourier分析方法，不难得到显式格式的稳定性条件是。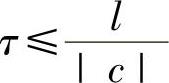

2.隐式格式

利用u（x，t）在点（i-1，n+1），（i，n+1），（i+1，n+1），（i，n），（i-1，n-1），（i，n-1），（i+1，n-1），7个结点上的值构造差分方程，网格点分布如图1.7.4所示。

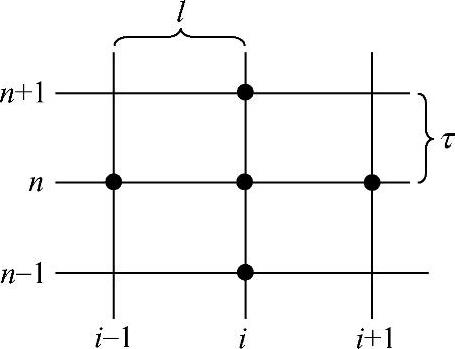
图1.7.3 显示格式

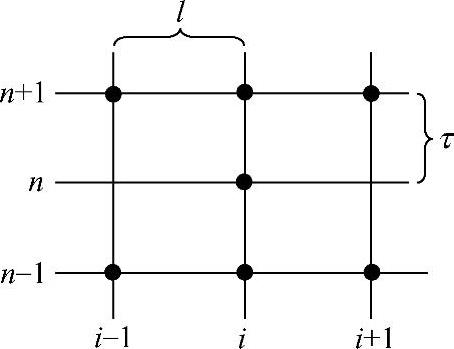
图1.7.4 隐式格式

现用待定系数法构造如下的差分算子L_nτ，令

L_nτ（uⁿ_i）=c₀uⁿ_i+c₁uⁿ⁺¹_i+1+c₂u^n-1_i+1+c₃uⁿ⁺¹_i-1+c₄u^n-1_i-1+c₅uⁿ_i⁺¹+c₆uⁿ_i^-1（1.7.7）式中，c₀，c₁，…，c₇为待定常数。

假定函数u（x，t）有四阶连续偏导数，按多元函数Taylor公式在点（i，n）展开u直到四阶偏导数项为止，有

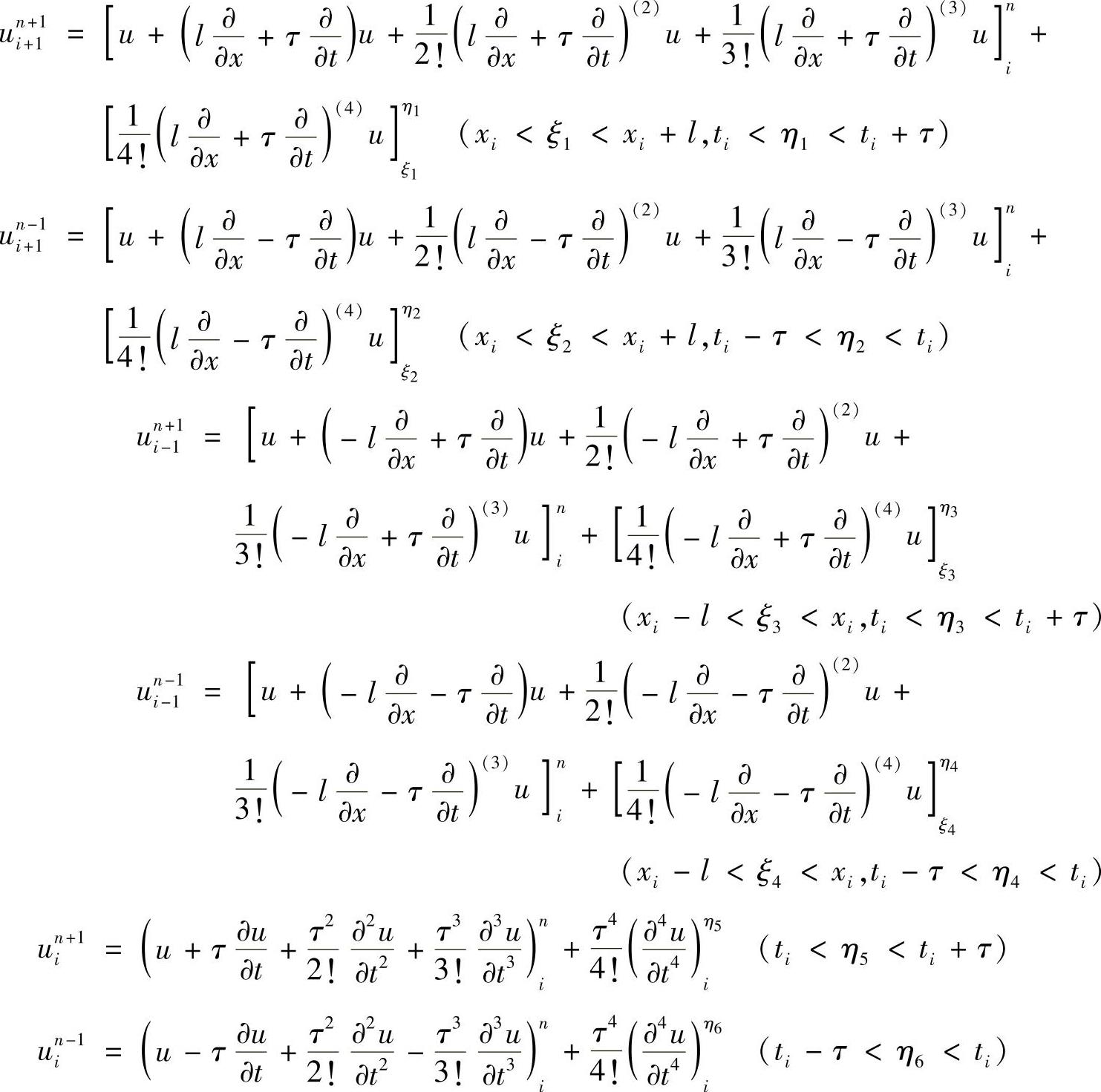
其中，

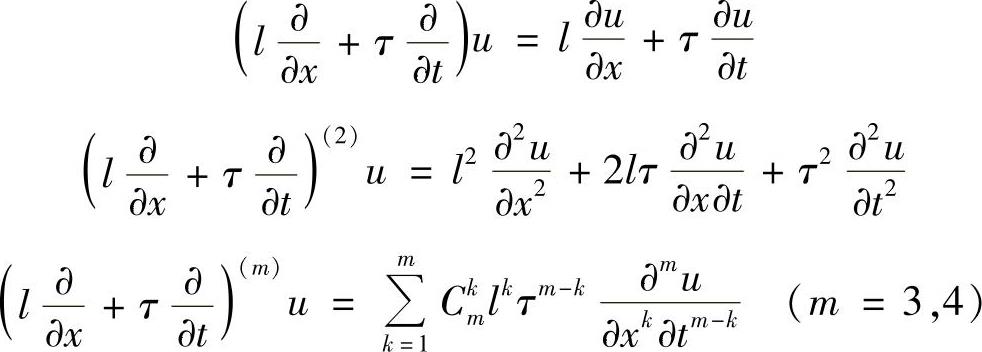(www.daowen.com)

将上列各式代入式（1.7.7）右端，合并同类项，令u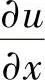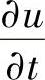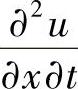，，，的系数为零，并使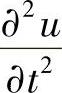的系数为-c²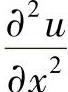，的系数为1，这样就可得到c₀，c₁，c₂，c₃，c₄，c₅，c₆所满足的代数方程组

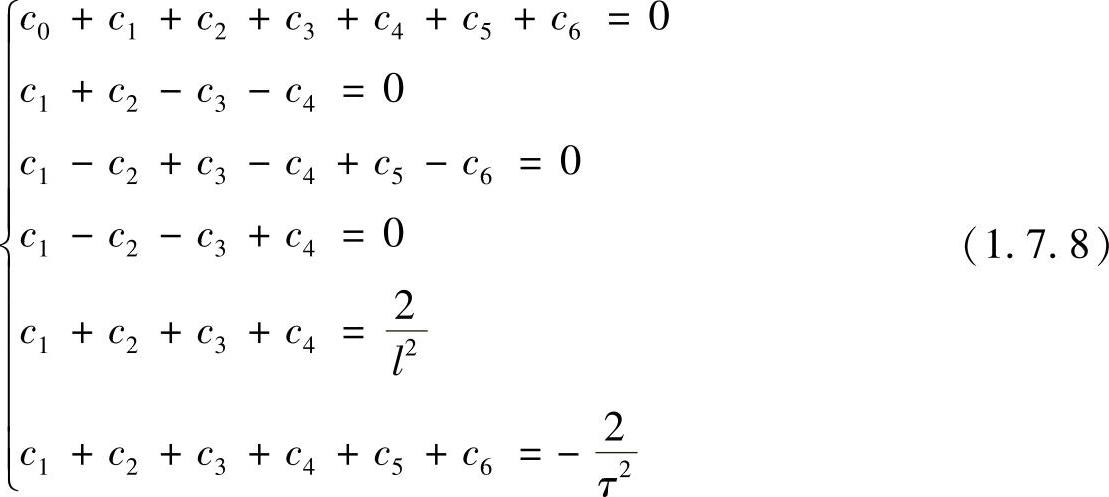
因为（i，n+1），（i，n-1）关于（i，n）对称，故还可补充一个方程

c₅=c₆

解以上方程组，得

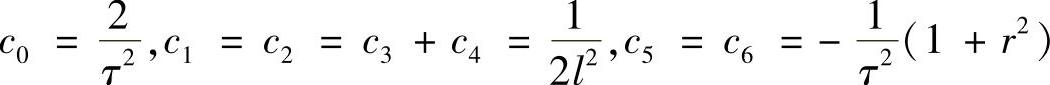
于是，式（1.7.7）可写为

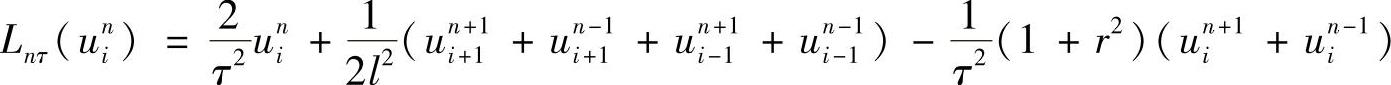
得到二阶波动方程（1.7.5）差分格式

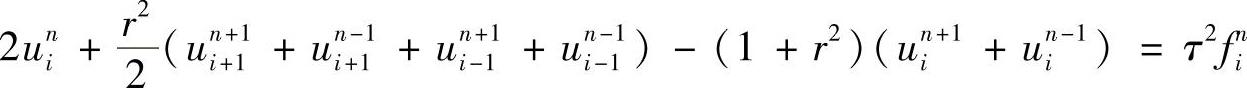
此即三层隐式差分格式，如第n-1层和第n层的值已经算得，为了求得第n+1层的值，必须解一个三对角的线性代数方程组，此格式的截断误差与格式（1.7.6）相同，为O（τ²+l²）。

3.Von Neumann格式

Von Neumann格式为九结点格式，其网格点分布如图1.7.5所示，其差分格式为

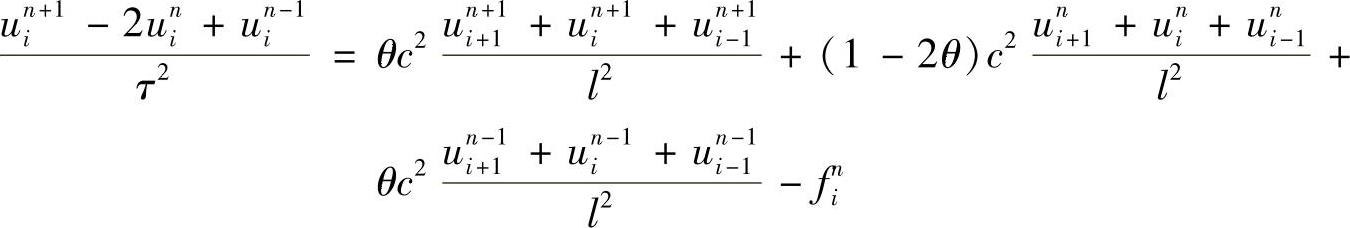
其中，0≤θ≤1是给定的参数，利用Taylor公式可直接验证，Von Neumann格式的截断误差为O（τ²+l²）。Von Neumann格式还可以改写为

θr²u_j+1ⁿ⁺¹ -（1+2θr²）u_jⁿ⁺¹+θr²uⁿ⁺¹_j-1=（2θ-1）r²u_jⁿ₊₁-2[（2θ-1）r²+1]u_jⁿ+

（2θ-1）r²u_jⁿ_-1-θr²u_j+1^n-1+（1+2θr²）u_j^n-1-θr²u_j-1^n-1+τ²f_jⁿ （1.7.9）

Von Neumann格式是三层隐式格式，当θ=0时，即为显式格式，若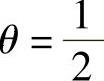，则为隐式格式，因此显式格式和隐式格式都是它的特殊情形。

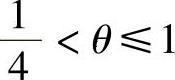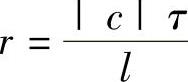应用稳定性的Fourier分析方法，可得，当时，无论取何值，Von Neumann格式都是稳定的。而当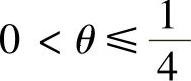时，Von Neumann格式的稳定条件是r满足

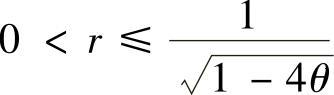
由于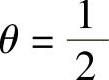时，Von Neumann格式成为隐式格式，所以隐式格式无条件稳定。

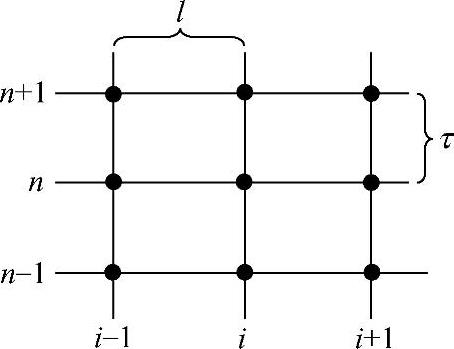
图1.7.5Von Neumann格式