用两组平行直线x=x_i=il，t=t_n=nτ分割成矩形网格，其中，l和τ分别为空间x和时间t的步长，交点（x_i，t_n）称为结点，对t=t_n上的全部结点称为差分网格的第n层。

一阶波动方程典型的差分格式，除了Lax格式（1.5.29）以外，还有偏心格式和LaxWendroff格式等，以下作简要介绍。

1.偏心格式

如果对时间步长τ和空间步长x均采用前差商，则对应于方程式（1.1.17）

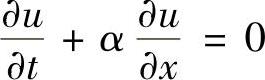
的差分方程写为

uⁿ_i⁺¹=（1+r）uⁿ_i-ruⁿ_i+1 （1.7.1）

其中，。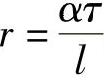

若对时间采用前差商，而对空间采用后差商，则得到

uⁿ_i⁺¹=（1-r）uⁿ_i+ruⁿ_i-1 （1.7.2）

关于显式差分式（1.7.1）和式（1.7.2）的稳定性，应用稳定性的Fourier分析方法，可得出，当α＞0时，显式差分式（1.7.1）不稳定；当α＜0，-1≤r≤0时，式（1.7.1）稳定。而对于格式（1.7.2）在α＜0时不稳定；当α＞0，0≤r≤1时，格式（1.7.2）稳定。根据CFL条件也可得出，当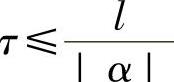时，两种格式都是稳定的。

综合上述分析，差分格式（1.7.1）和式（1.7.2）是否稳定与微分方程式（1.1.17）的系数α的符号有关。我们知道，方程式（1.1.17）有一特征线

x-αt=C（C为常数）

当α＞0时，特征线向右倾斜，当α＜0时，特征线向左倾斜，因此，所构造的差分格式是否稳定实质上与特征线的走向有关。差分格式（1.7.1）和式（1.7.2）的图分别如图1.7.1和图1.7.2所示。

由稳定性分析可知，若所构造的差分格式与微分方程的特征线的走向一致，则在r满足一定条件下是稳定的；反之，不论r如何都是不稳定的。事实上，当α＞0时，过点（i，n+1）的特征线与t=t_i的交点定落在点（i，n）的左侧；当α＜0时，过点（i，n+1）的特征线与t=t_i的交点定落在点（i，n）的右侧。故差分格式（1.7.1）和式（1.7.2）分别称为“右偏心”格式和“左偏心”格式。

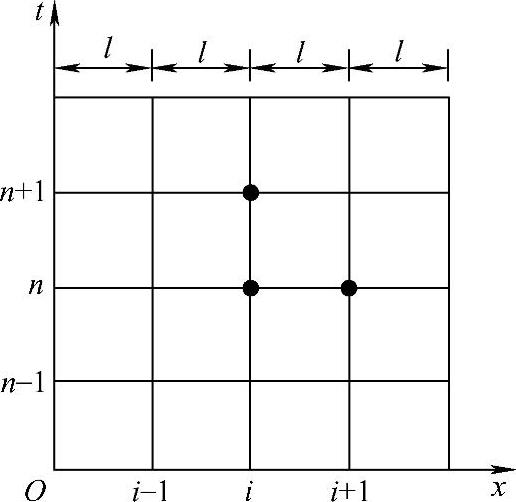
图1.7.1 时间前差空间前差(www.daowen.com)

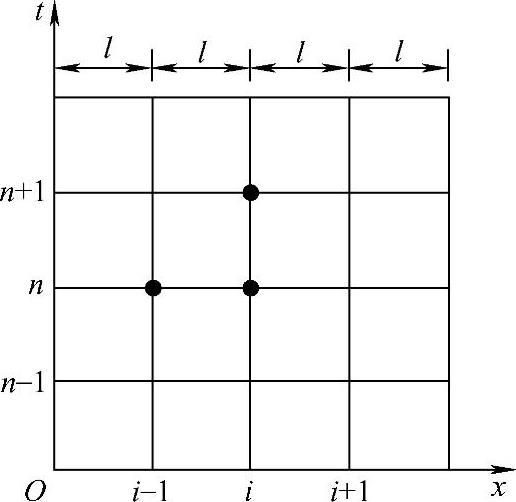
图1.7.2 时间前差空间后差

2.LaxWendroff格式（LW格式）

LW格式为

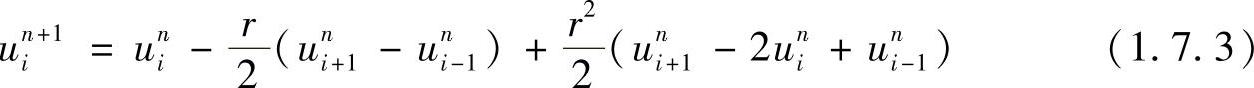
为了构造格式（1.7.3），利用对时间的Taylor展开，可得

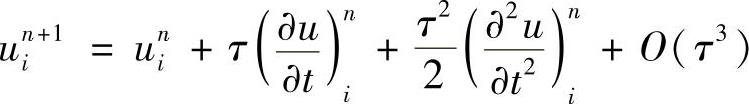
利用微分方程（1.1.17），得到

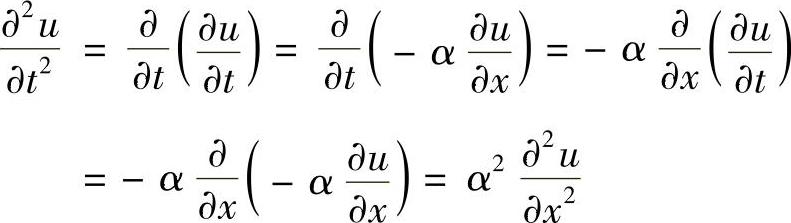
于是，有

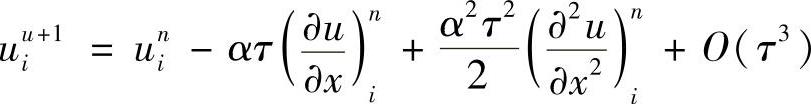
再利用中心差分公式

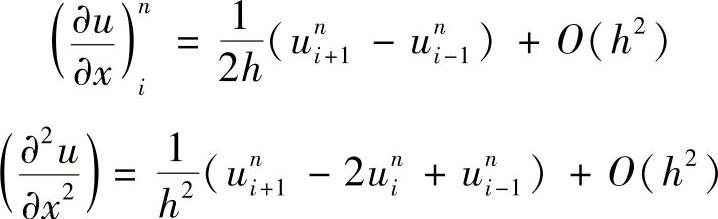
略去高阶误差项，则得到我们所要构造的差分格式（1.7.3），其截断误差是O（τ²+h²）。

应用稳定性的Fourier分析方法，可得出，当|r|≤1，即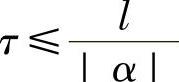时，LW格式满足CFL条件，其差分问题的解是稳定的。