以圆柱体内稳态导热问题为例进行分析，我们知道，若忽略温度沿圆柱长度方向的变化，则温度只是两个空间变量的函数，即T=T（ρ，φ）。温度场所处的几何区域是圆域、圆环域和扇形域，如图1.6.3所示。含有内热源的稳态导热的泛定方程为

对这种几何区域进行离散化时，直接应用矩形网格显然不合适。这里介绍两种处理方法，其中一种是采用经典的保角变换方法，把圆形的几何区域变换为矩形区域；另一种方法是从圆环形区域出发，采用坐标正交曲线簇将区域网格化，建立相应的差分方程。

图1.6.3 非矩形计算域

在复变函数论中已证明，若在z=x+iy平面上给定Φ（x，y）的拉普拉斯方程边值问题

经过保角变换w=f（z）后，原边值问题转化为w=u（x，y）+iv（x，y）平面上Φ（u，v）拉普拉斯方程的边值问题

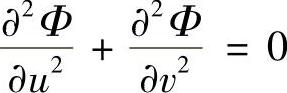
与上述结论类似，若在z=x+iy平面上给定Φ（x，y）的泊松方程边值问题

在单值解析函数w=f（z）变换下，原边值问题转化为w=u（x，y）+iv（x，y）平面上Φ（u，v）的泊松方程边值问题

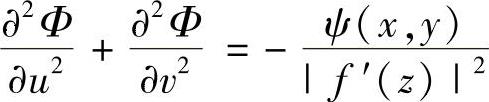
只是在保角变换w=f（z）下，泊松方程中的源的强度发生变化。

对于圆域、圆环域和扇形域内的边值问题，引进坐标变量ξ代替原有坐标变量ρ，令ξ=lnρ（暂不考虑ρ=0的情形），于是式（1.6.10）中的一阶微商与二阶微商可以表示为

式（1.6.10）成为(www.daowen.com)

对于无内热源问题，有

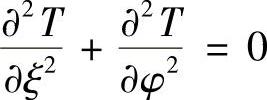
这样，对环形区域经过坐标变换可变成矩形区域，进而就可用矩形网格建立差分方程。如图1.6.4所示，取四分之一圆环区域内的网格线ρ=常数，φ=常数，将区域等分，即Δρ与Δφ均为等步长的。经过ξ=lnρ变换后，扇形域变成矩形域，结点位置也有对应的关系。在新的矩形区域内，Δφ仍保持其等步长的特性，而Δρ变成Δξ后，不再是等步长了。相反，若要保证矩形域内等步长，在环形域内就不可能是等步长。

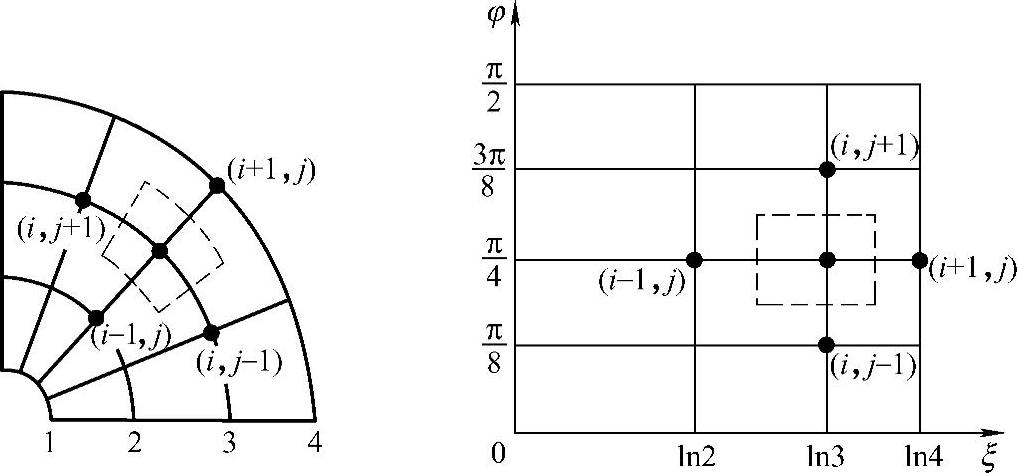
图1.6.4 环形区域变换为矩形区域

采用保角变换方法处理圆域、圆环域和扇形域内的边值问题时，在实际计算中要作变步长的运算，较为繁琐。以下直接从式（1.6.10）出发，以差商代替微商来获得差分格式。一阶微商与二阶微商表示为

式中，一阶微商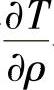与二阶微商的截断误差均为O[（Δρ）2]。

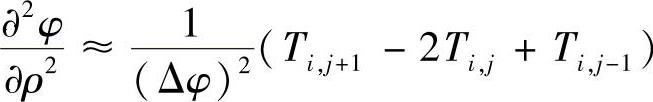
将以上差商式代入式（1.6.10），有

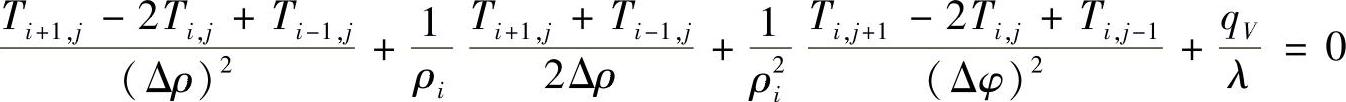
此即圆环域内结点的差分方程。该差分方程也可以通过圆环域单元体的热平衡关系来建立，所取的单元体如图1.6.4中的虚线所示，列出平衡关系为

边界结点差分方程的建立方法与矩形区域也大致相同，可采用边界条件中的微商用差商代替直接得到差分方程，也可采用边界单元体的热平衡法来得到差分方程，这里不再赘述。