前面所讨论的差分格式是基于均匀网格基础上的，以下针对一般的二阶椭圆型微分方程，考虑如何建立它在非均匀网格上的差分格式。

考查如下的边值问题

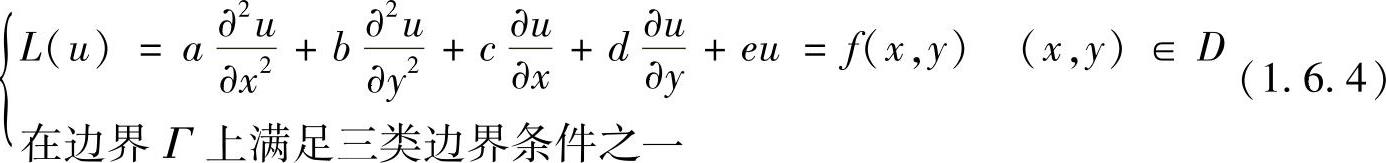
其中，D是具有边界Γ的有界区域；a，b，c，d，e均为x，y的已知函数；a（x，y），b（x，y），c（x，y），d（x，y），e（x，y）和f（x，y）在D+Γ上连续，且a（x，y）≥a₀＞0，b（x，y）≥b₀＞0，e（x，y）≤0。

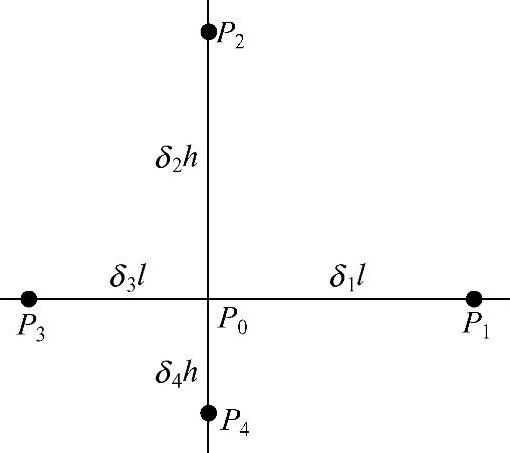
图1.6.2 非均匀网格

设有非均匀网格

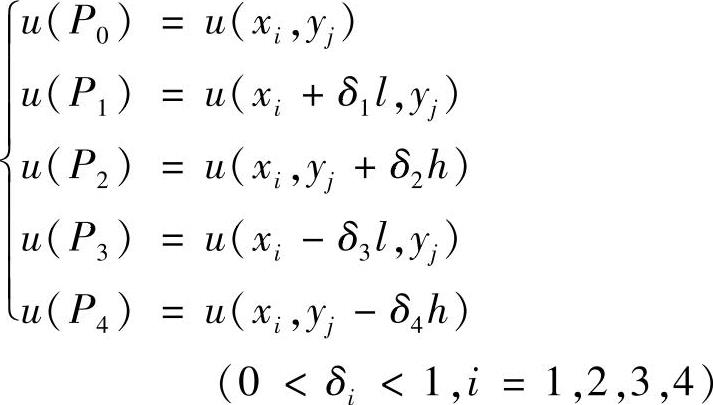
如图1.6.2所示。采用待定系数法构造非均匀网格的差分格式。引入差分算子L_δhl，令

L_δlh（u₀）=c₀u₀+c₁u₁+c₂u₂+c₃u₃+c₄u₄ （1.6.5）

其中，u_i=u（P_i）（i=0，1，2，3，4），c_i为待定常数。

由Taylor展开，有

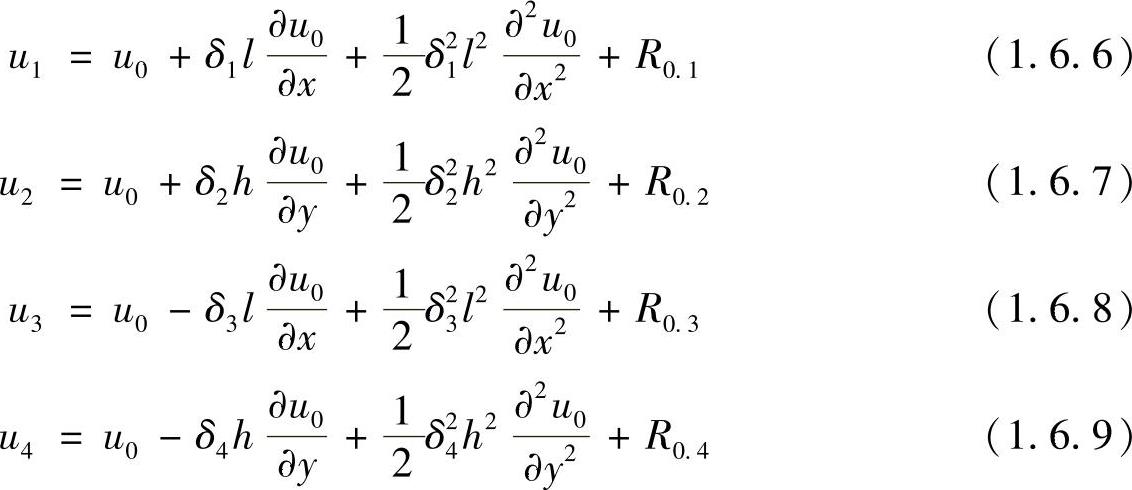
其中，(www.daowen.com)

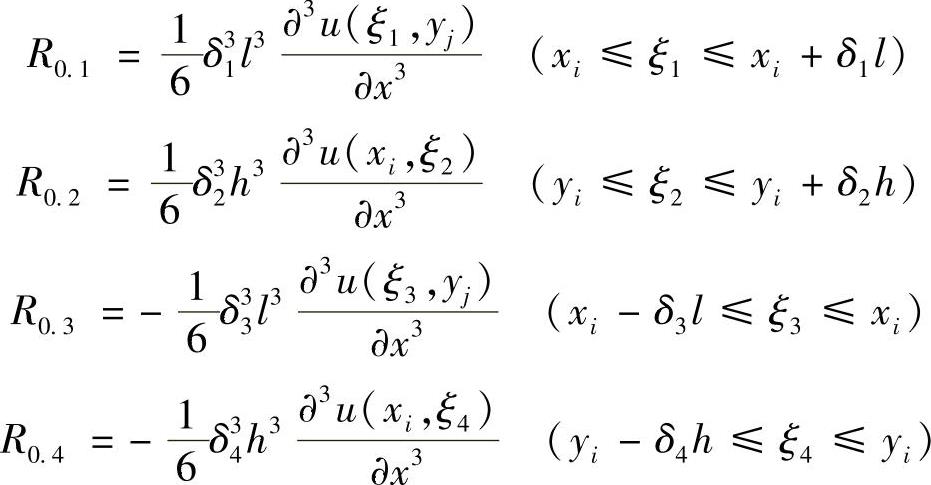
将式（1.6.6）～式（1.6.9）代入式（1.6.5），得

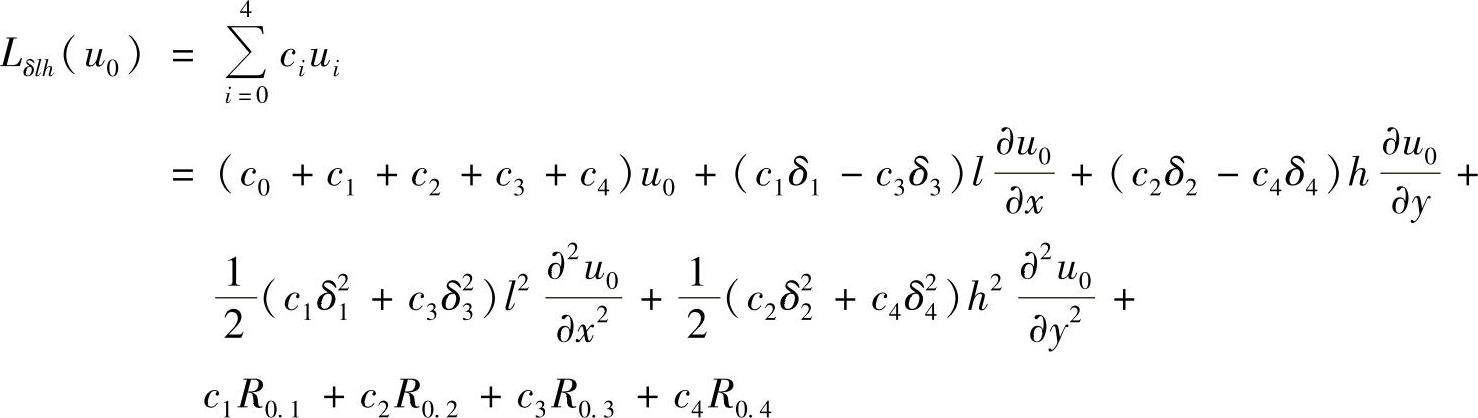
为了使L_δlh（u₀）可作为L（u₀）的逼近，与方程

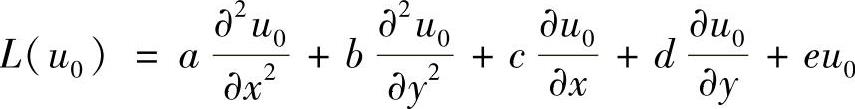
比较，令系数对应相等，此即所谓的待定系数法。于是

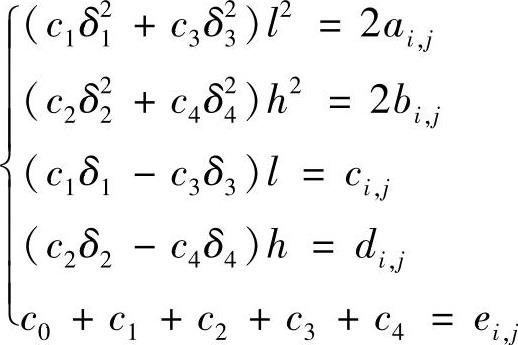
解方程组，得到

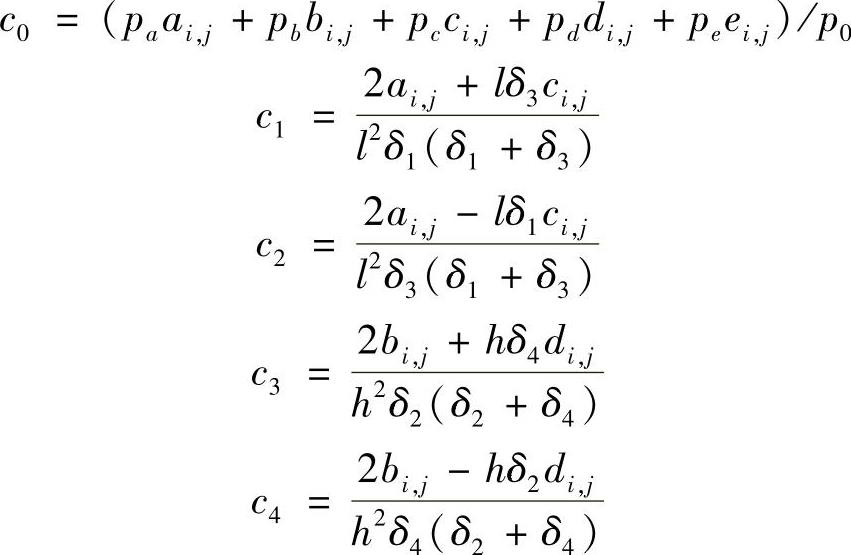
其中，p₀=l²h²δ₁δ₂δ₃δ₄，p_a=-2h²δ₂δ₄，p_b=-2l²δ₁δ₃，p_c=-lh²δ₂δ₄（δ₃-δ₁），p_d=-l²hδ₁δ₃（δ₄-δ₂）。将这些系数代入式（1.6.5）所得到的差分算子L_δlh（u₀）逼近微分算子L（u₀），其截断误差为O（l+h）。

也可利用非均匀网格下的一阶和二阶差商来逼近导数。在图1.6.1中，采用下面的差商

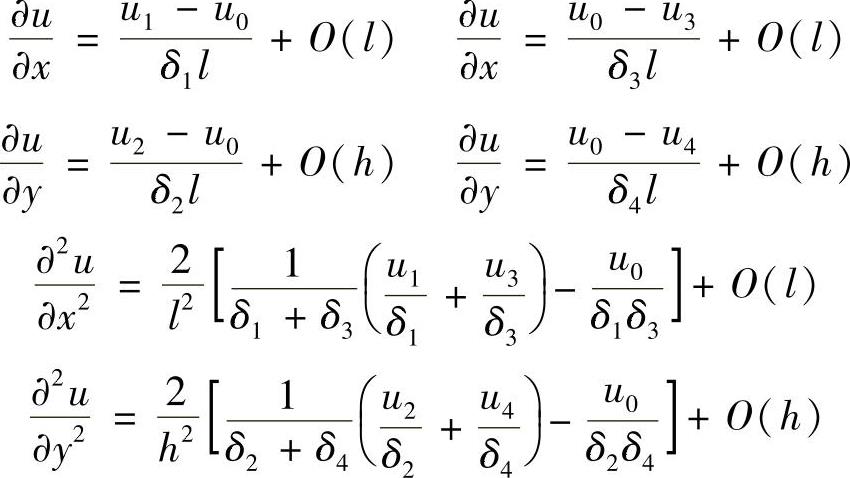
根据网格点所在的位置，选取上述不同的表达式代入微分方程，即得到在非均匀网格下的差分方程。