在1.3节我们已经对泊松方程离散化，并建立了有限差分格式（1.3.3）

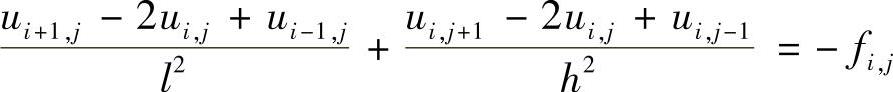
其中，f_i，j=f（x_i，y_i）。

上式可以改写为

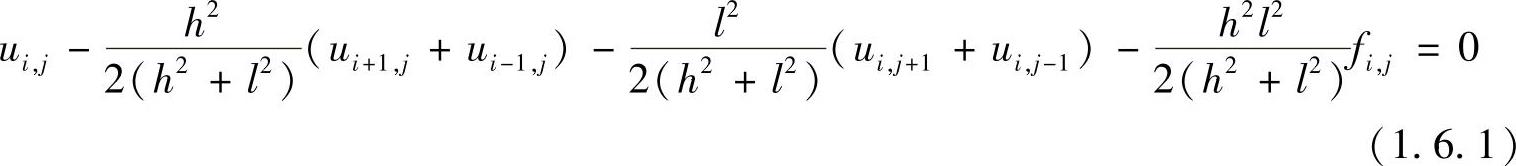
式（1.6.1）称为五点差分格式。其特点是每一个方程最多包含五个点处的函数值，而且这些点的分布是有规律的，即与点（i，j）相应的方程只和该点的上、下、左、右4个相邻的结点有关，如图1.6.1所示。

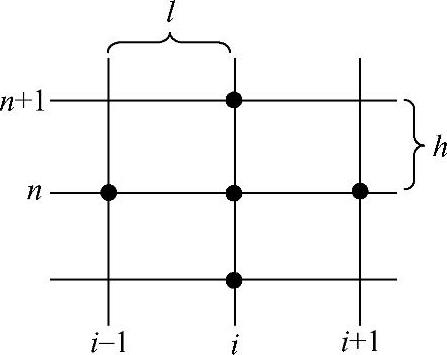
图1.6.1 五点差分格式

特别地，对于拉普拉斯方程，我们还可得到差分格式

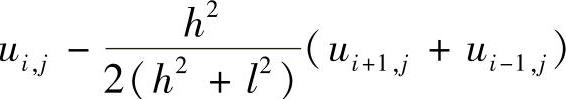(www.daowen.com)

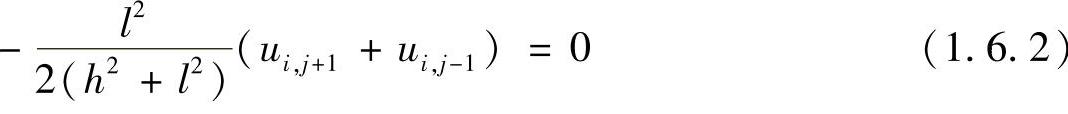
可以证明以上关于椭圆型方程的五点格式差分解的存在性和唯一性。为了叙述方便，引入差分算子L_hl，使

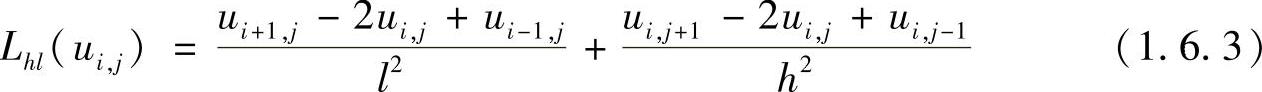
极值原理：设u_i，j是定义在网格点上的一组值，且u_i，j不全部相等。如L_hlu_i，j≥0，则u_i，j在内部结点上的最大值不大于边界上的最大值；如L_hlu_i，j≤0，则u_i，j在内部结点上的最小值将大于边界上的最小值。

证明：当L_hl（u_i，j）≥0时，若u_i，j是最大值，且最大值为M，则有

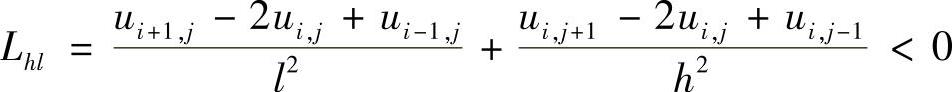
这与L_hlu_i，j≥0相矛盾，所以u_i，j不可能在内部结点取最大值，即周围四点中至少有一点的函数值小于M，因此，这时u_i，j在内部结点上的最大值不大于边界上的最大值。用类似的方法可以论证极值原理的后半部分。

根据极值原理，可以直接推出差分方程式（1.6.1）存在唯一解。亊实上，如果差分方程式（1.6.1）有两个适合同一边界条件的解，则这两个解的差，本身也是该差分方程问题的解，并且在边界上处处为零，由极值原理可知，这样的解必须恒等于零，因此，解的唯一性成立。

对于五点有限差分格式的收敛性，从极值原理出发可推证，若微分方程问题的解u（x，y）在区域D+Γ四阶连续偏导数，则五点差分格式收敛，证明从略。