当偏微分方程采用某种差分格式转化为差分方程后，要求当时间步长τ→0和空间步长l→0时，这个差分方程能与微分方程充分接近，也就是要求当τ→0，l→0时，差分方程的截断误差在任一网格上均应趋于零，称这样的差分方程和与之对应的偏微分方程相容。只有保证相容性，才能使得当τ→0，l→0时，差分方程的解在每个网格结点上都收敛于偏微分方程的解。判断相容性的条件就是当步长τ→0，l→0时，差分方程的截断误差Rⁿ_i→0。下面仍以一维非稳态热传导问题为例来说明相容性的具体检验方法。在式（1.3.7）中，时间项和二阶空间导数项均用中心差分近似，有

在式（1.5.1）中，以Tⁿ_i⁺¹+Tⁿ_i^-1替换2Tⁿ_i，则有

差分方程式（1.5.2）是另外一种差分格式，这里引入这种格式的目的仅在于考查其与原偏微分方程的相容性。分析差分方程式（1.5.2）的截断误差，由Taylor展开式，得

以及

于是截断误差(www.daowen.com)

显然，若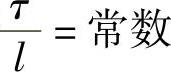，则当τ→0，l→0时，截断误差不趋近于0，因此，差分方程式（1.5.2）与微分方程式（1.3.7）不相容。

若选用显式差分格式（1.3.7），其截断误差为

当τ→0，l→0时，截断误差趋近于0，因此，在这种情况下，差分方程式（1.3.8）与微分方程式（1.3.7）相容。

相容性概念是差分方法中最基本的概念，一般说来，要用差分格式求解偏微分方程问题，相容性条件必须满足。