上一节我们采用积分恒等式法建立了内部单元的差分格式，这种方法同样适用于边界单元。下面仍以稳态热传导问题为例，介绍这种方法，计算域如图1.4.7所示。

若泛定方程式（1.3.8）的边界条件为

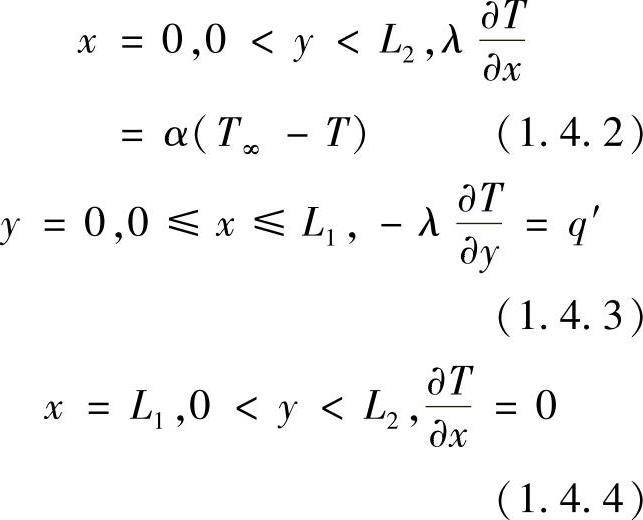
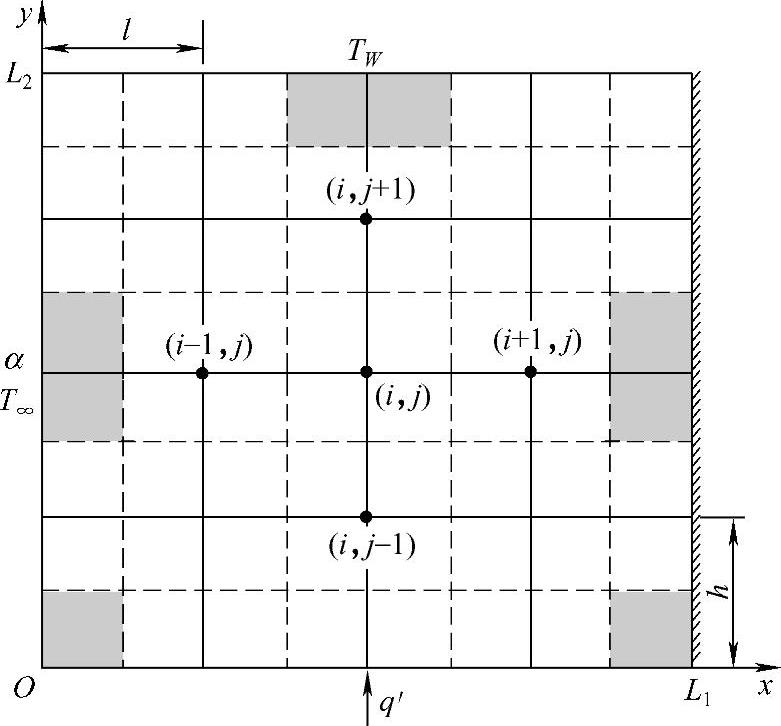
图1.4.7 计算域与边界条件

y=L₂，0≤x≤L₁，T=T_W （1.4.5）

式中，α为热传递系数；q′为热流密度；T_W为边界温度；T_∞为环境温度。以下我们从边界单元体的热平衡原理出发，写出代数形式的差分方程。

对于对流边界单元，如图1.4.8所示，将基于能量守恒原理的积分形式的导热方程直接应用于每个单元，可得到如下差分方程

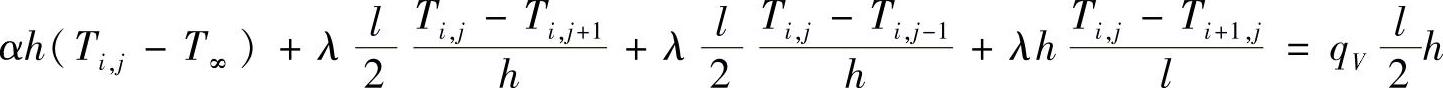
对于热流边界单元，如图1.4.9所示，可得到如下差分方程

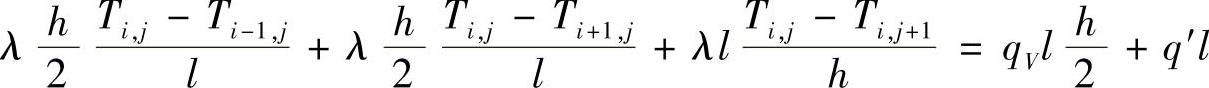
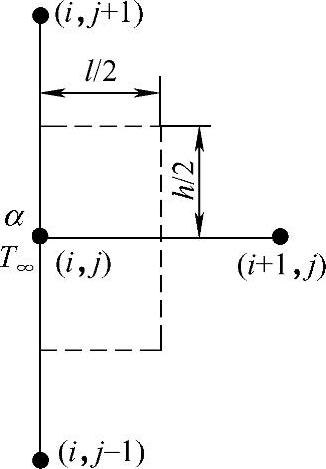
图1.4.8 对流边界单元

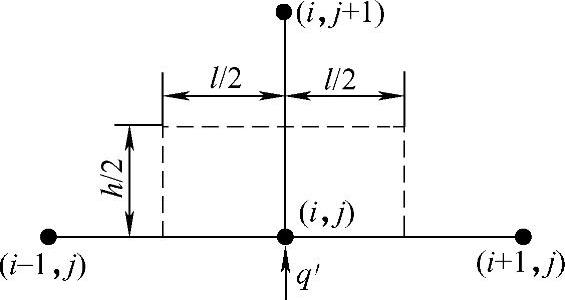
图1.4.9 热流边界单元(www.daowen.com)

对于绝热边界单元，如图1.4.10所示，可得到如下差分方程

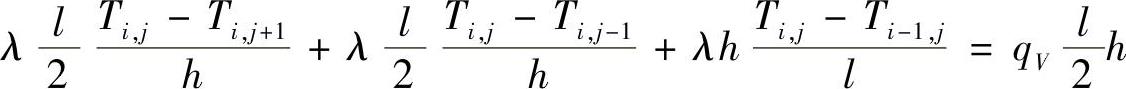
对于温度给定的边界单元，如图1.4.11所示，可直接写出差分格式

T_i，j=TW

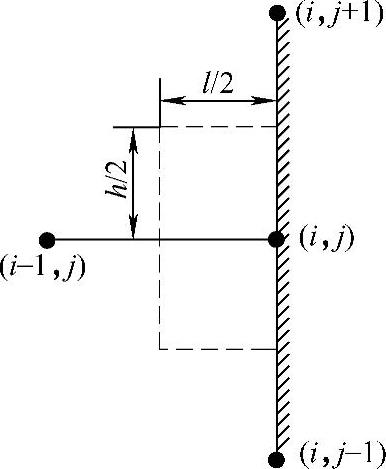
图1.4.10 绝热边界单元

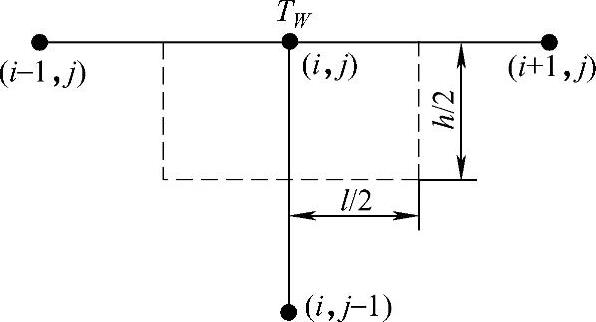
图1.4.11 温度给定边界单元

对于图1.4.7中四个角上的边界单元，它们的两个外边界从属于两种边界条件，其中一个为对流边界，另一个为热流边界，如图1.4.12所示，不难得到如下差分方程

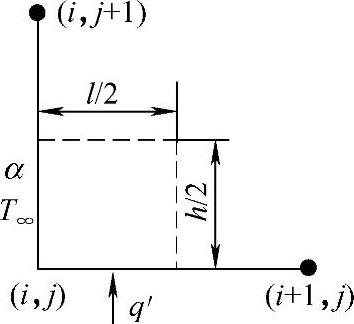
图1.4.12 具有两类边界的单元

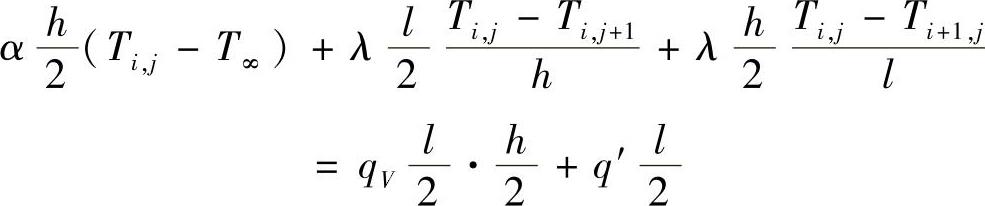
从以上内容可以看到，对应同一个边界条件，引用不同的差分方法，得到几乎完全不同的差分方程，这种数学上的不同反映了两种差分方法的根本区别。采用积分恒等式法建立边界差分方程，较之于只从数学形式上用差商代替微商建立边界差分方程的方法，前者更忠实于原来的物理模型，我们有理由相信，采用积分恒等式法得到的差分方程，其计算结果更符合实际。

经过以上边界条件处理后，对每一个边界点都可以列出一个差分方程，再与各内点处的差分方程联立，就构成了方程个数与未知数个数相同的线性代数方程组。