【摘要】：对于第一类边界条件，主要有两种不同精度的处理方法。图1.4.3 直接转移第二种方法是线性插值。对于图1.4.3中的点P，可取B和C两点或Q和R两点作线性插值或一次插值的截断误差为O或O。于是，在结点P处，有但点C一般不是结点，因此需要以点B和点E的值作线性插值，来近似表示u，即于是进一步近似，取由点Q的第三类边界条件最终得到点P的差分方程为
一般情况下，边界Γ是一条曲线，并且不和差分网格结点吻合，需要作近似处理才能达到要求的计算精度。对于第一类边界条件，主要有两种不同精度的处理方法。
第一种方法是零次插值，也称做直接转移，这是一种最简单的近似处理方法，如图1.4.3所示。若边界结点S正好落在边界Γ上，此时有
uS=φ（S）
若边界点P不在边界Γ上，可在边界Γ上取一个与点P最靠近的网格线上的点，如图1.4.3中的点R，以φ（R）近似代替，即uP=φ（R）。零次插值的局部误差为O（h）或O（l）。
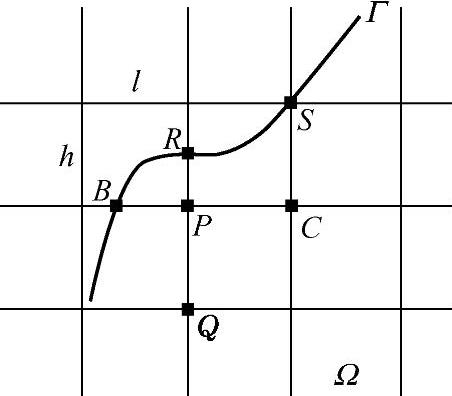
图1.4.3 直接转移
第二种方法是线性插值。对于图1.4.3中的点P，可取B和C两点或Q和R两点作线性插值
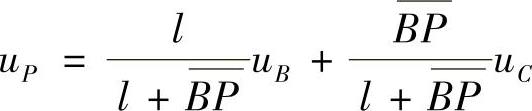
或
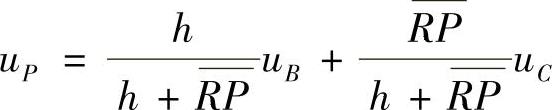
一次插值的截断误差为O（l2）或O（h2）。
对于第二、第三类边界条件，处理方法有多种，这里介绍比较简单的处理方法，为了叙述方便，采用正方形网格，即l=h。
若外法向与坐标轴平行，如图1.4.4所示，此时，分别有
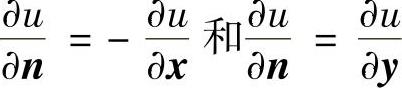
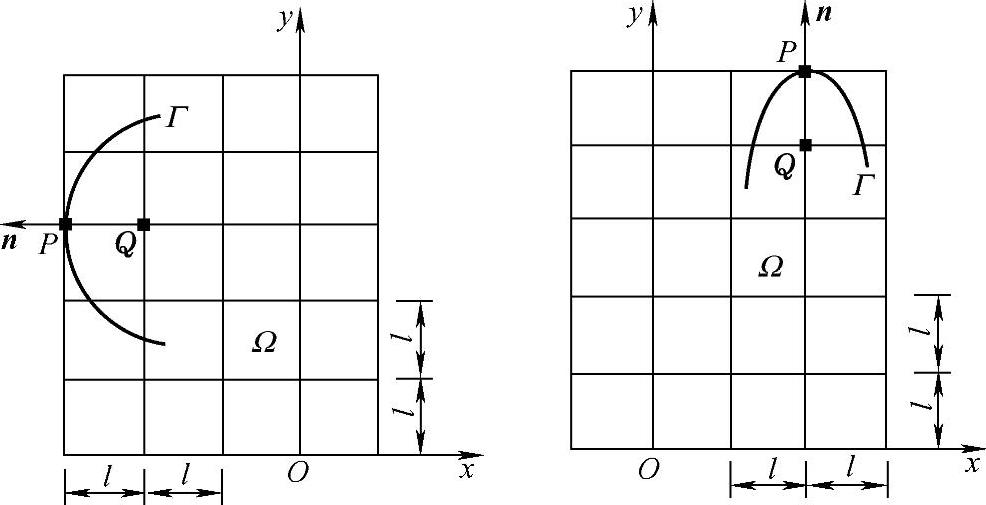
图1.4.4 外法向与坐标轴平行
于是，边界结点P的第三类边界条件可离散化为
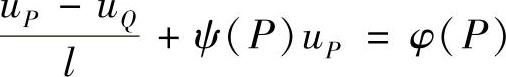
若外法线与坐标轴方向不平行，如图1.4.5所示，则
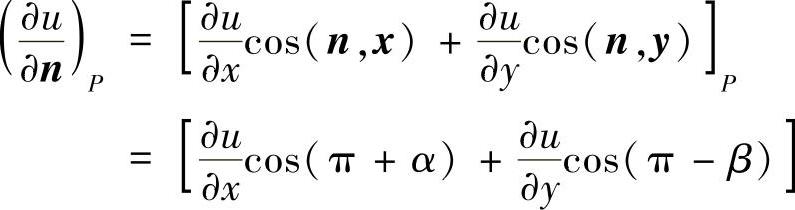(www.daowen.com)
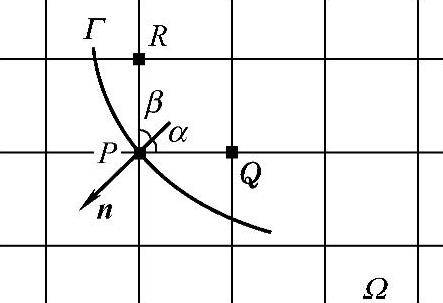
图1.4.5 外法向与坐标轴不平行
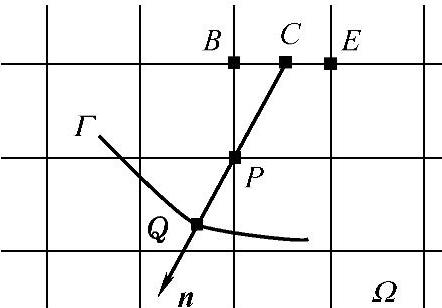
图1.4.6 边界点处理
于是，边界结点P的第三类边界条件可离散化为
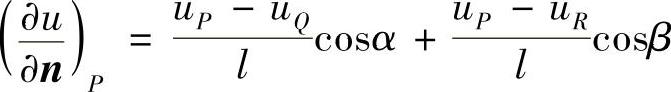
若边界点P不在边界Γ上，如图1.4.6所示，此时，过点P作边界Γ的外法线，交边界Γ于点Q，另一端交网格线于点C。显然，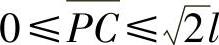
，
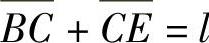。于是，在结点P处，有
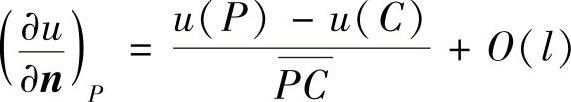
但点C一般不是结点，因此需要以点B和点E的值作线性插值，来近似表示u（C），即
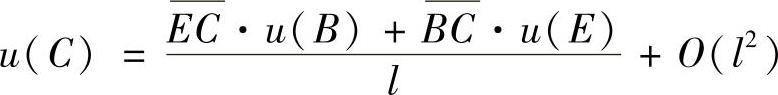
于是
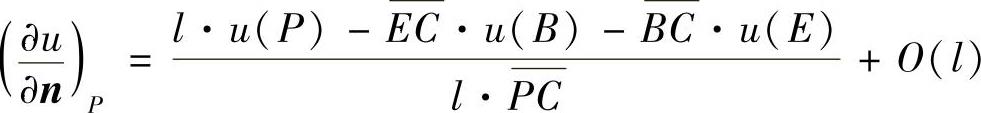
进一步近似，取
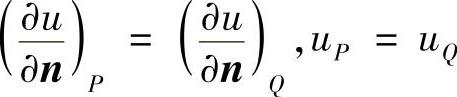
由点Q的第三类边界条件
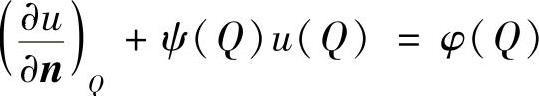
最终得到点P的差分方程为
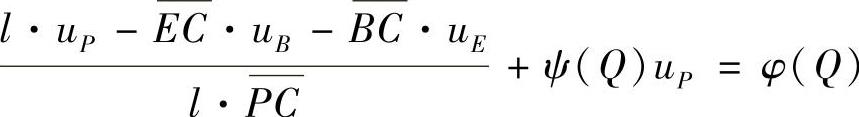
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
