下面以椭圆型方程为例,介绍边界条件的处理方法。我们知道,用差分法求解边值问题的目的是求出Ω=D+Γ中各结点处的近似解,未知量ui,j的个数即为Ω中的结点数。为了确定这些未知量,需建立相同个数的差分方程。通常有限差分格式是在计算域的内点上建立的,差分方程的个数一般少于未知量的个数。为此,需对边界条件进行近似处理以补充差分方程。
为了便于讨论,假定所研究的计算域Ω是矩形域(0≤x≤a,0≤y≤b),如图1.4.1所示,并分成等步长网格,a=(I+1)l,b=(J+1)h,这时边界结点都落在矩形的边界上,对于第一类边界条件,边界上的值为已知,则计算域内共有内点I×J个,而边界结点为2(I+J+2)个,对于每一个内点可列一个差分方程式,共有I×J个差分方程式,可解出I×J个内点的未知量。
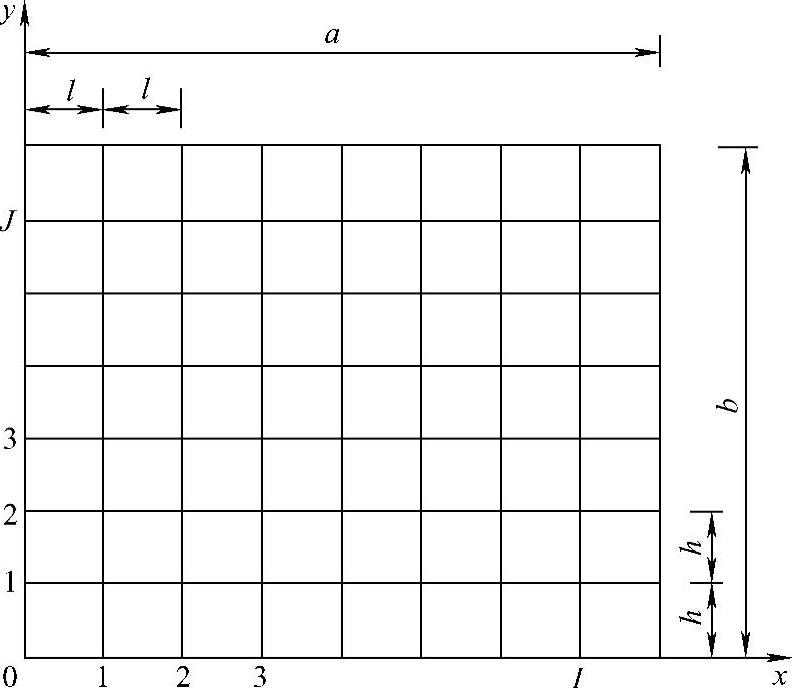
图1.4.1 矩形计算域及其网格划分
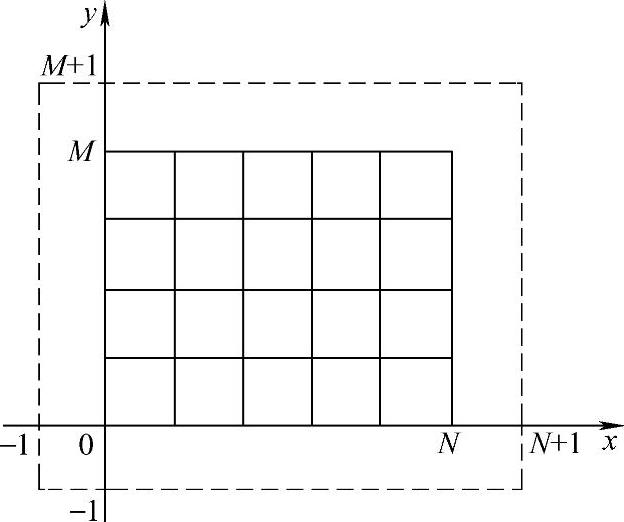
图1.4.2 边界网格划分
对于第二类和第三类边界条件,边界上的值未知,这时未知数共有
I×J+2(I+J+2)
=(I+2)(J+2)
由计算域内点列出I×J个方程,另外需要列出边界结点的2(I+J+2)个方程。(https://www.daowen.com)
若在x方向划分成N等分,在y方向划分成M等分,如图1.4.2所示。对于第一类边界条件,即u|Γ=φ(x,y),只需取
ui,j=φi,j,(xi,yj)∈Γ
对于第二类边界条件,即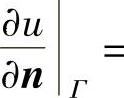
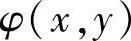 ,需在矩形计算域Ω的四周虚设一排结点,然后在边界点处采用中心差分格式离散化边界条件,有
,需在矩形计算域Ω的四周虚设一排结点,然后在边界点处采用中心差分格式离散化边界条件,有
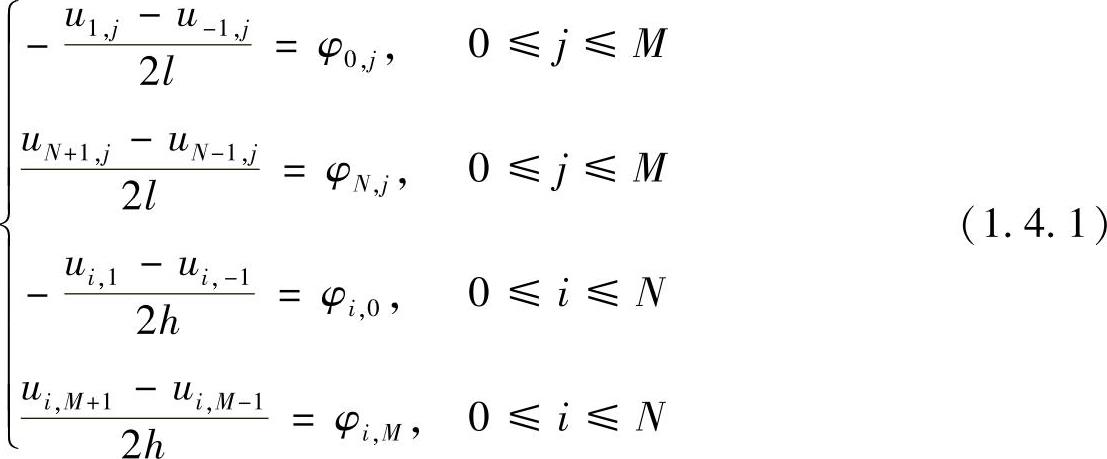
其中,u-1,j,uN+1,j,ui,-1和ui,M+1均为虚设的值。
按照此前建立的差分格式建立四周边界网格点上的差分方程,然后与式(1.3.11)联立,消去这些附加的函数值,之后再与内点上建立的差分方程联立,得到所需的线性代数方程组。
对于第三类边界条件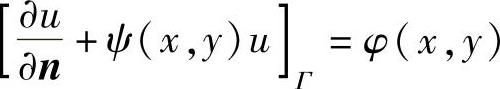 ,处理方法与第二类边界条件类似,不难列出相应边界条件的格式为
,处理方法与第二类边界条件类似,不难列出相应边界条件的格式为
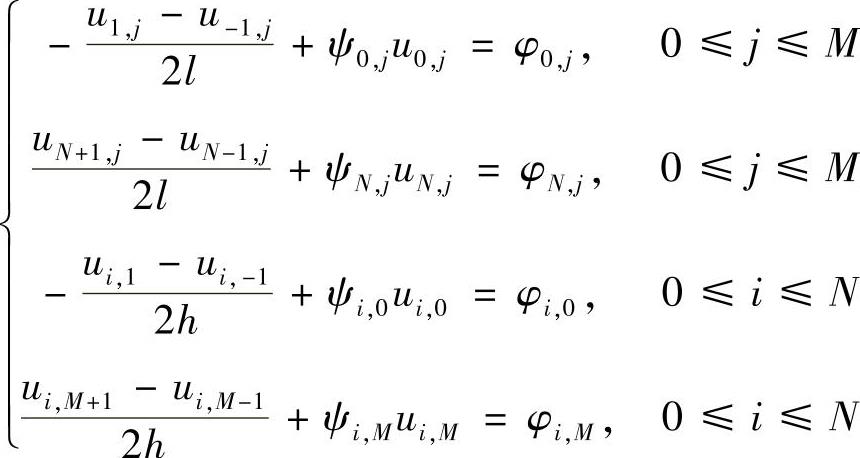
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






