以上我们从偏微分方程出发，以差商代替微商，建立有限差分格式。本小节我们从积分形式出发，建立差分格式，这种构建差分格式的基本思想与我们将在第4章讨论的有限体积法的基本思想是一致的。我们知道，很多物理现象和运动过程一般都服从某种守恒规律，因此，描述它们数量关系的微分方程也具守恒性。由于某些守恒性可用积分形式表达，尤其对守恒型微分方程进行积分，可以转化成积分方程或微分积分方程，在此基础上，我们用数值积分公式来代替积分，就得到差分方程，这种构造差分方程的方法称为积分恒等式法。下面以稳态热传导问题为例，介绍这种方法。控制方程为

式中，q_V为热源强度，即单位时间单位体积内的发热量；λ为导热系数。

我们讨论矩形区域内稳态温度分布，计算域如图1.3.4所示。这里只是处理方法略有改变，不是从微分方程的边值问题出发，而是从积分方程式入手，但处理的步骤大致相同。将区域离散化，构成有限个单元体，将能量守恒的积分形式应用到每个单元体，得到差分方程，最后构成差分格式。下面按步骤予以说明。

第一步是区域离散化，方法是整个区域划分成有限个小单元体。原则上讲，这种划分有相当的任意性，只要每个小单元体在整个域内形成一个无遗漏、无重复的覆盖即可。由于所讨论的问题是矩形区域，显然划分成一系列矩形方块是最适宜的。用虚线对图1.3.4所示的矩形域进行划分，由虚线框围成的小矩形或虚线与边界线所围成的小矩形为一个单元，这些单元覆盖了整个区域。每个单元内温度、热容一般都是坐标的分布函数。若单元足够小，则其中某一点温度就可以代表整个单元的温度，这些点也称之“结点”，一个结点对应一个单元。图1.3.4的矩形区域被划分成25个小单元，i=1，2，3，4，5；j=1，2，3，4，5。

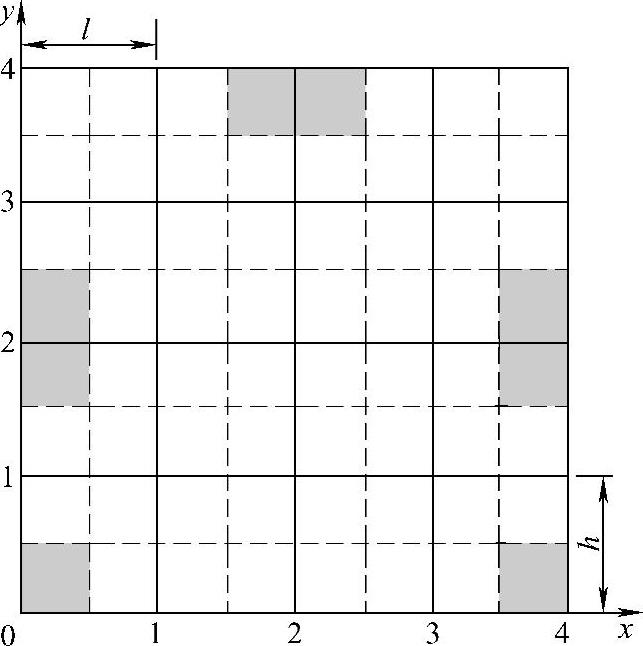
图1.3.4 矩形域单元划分

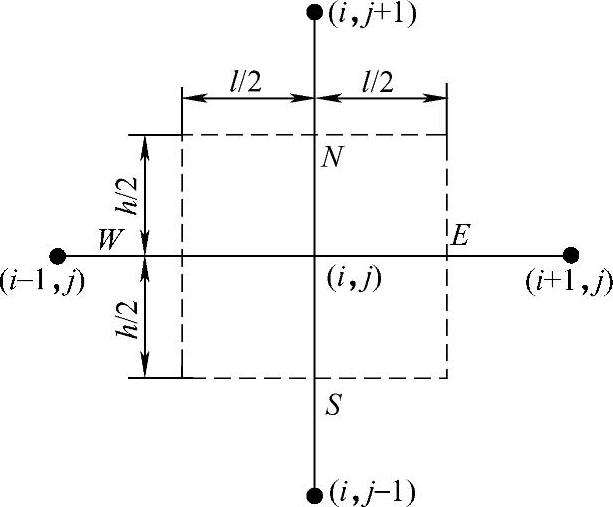
图1.3.5 内部单元

第二步是列出单元的差分方程，方法是把表示能量守恒的方程应用到每个单元。对于内部单元，即边界都在区域内部的单元，如图1.3.5所示。由图1.3.4中划出的第（i，j）单元，i=2，3，4，j=2，3，4，都是内单元。根据能量守恒定律，取物体内单元体V内单位时间产生的热量等于同时间内通过单元体界面S传导带走的热量，即满足如下数学表达式

式中，n为单元体界面的外法线方向的单位矢量；S是单元体的边界面积。将式（1.3.9）应用到（i，j）单元时，V=lh，S=2l+2h，式（1.3.9）可写成如下形式(www.daowen.com)

Q_E+Q_W+Q_N+Q_S=q_V·lh （1.3.10）

式中，Q_E，Q_W，Q_N和Q_S分别为（i，j）单元在单位时间内从单元体的四个边界面导出的热量，分别是

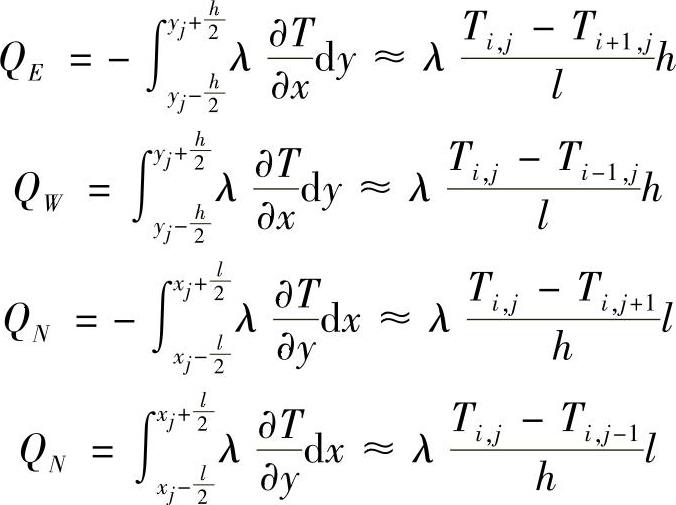
将Q_E，Q_W，Q_N和Q_S的表达式代入到式（1.3.10）中，可得

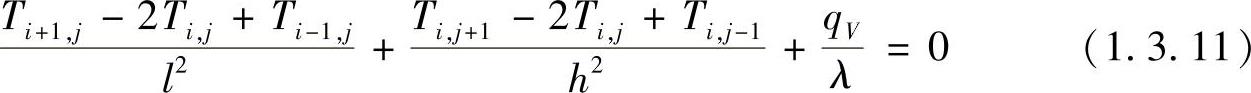
这是内单元的差分方程，与式（1.3.3）的内结点差分方程完全一致，这一事实说明用微分形式或积分形式描述物体内导热时，其实质是相同的。应当指出，尽管用微分形式与积分形式所得到的差分方程在形式上完全相同，但它们所依赖的数学基础有所不同。从微分方程出发得到的差分方程，要求区域内温度分布光滑连续，而积分形式则是要求每个单元边界上热流可积，这样，采用积分形式推导差分方程比微分形式要求的温度分布光滑连续显然放宽了。如果区域由导热系数不同的两种物体构成，并在交界面上有接触热阻，或者物体内部存在缝隙，则在交界面或缝隙处温度分布就不连续或不光滑，在这种情况下，用积分形式的有限差分法，只需在单元划分时使那些交界面正好落在单元的变截面即可。还应当指出，在Q_E，Q_W，Q_N和Q_S的表达式中的近似等号表示越过单元边界的热流正比于相邻的两单元的温差，由于假定用单元内某点的温度代表单元整体温度，因此就包含着一定的误差，其误差的量级为O（l）或O（h），这种误差表现在单元的差分方程上包含有O（l²+h²）量级的截断误差。

以上在推导内结点差分方程式（1.3.11）过程中，先是把能量守恒原则应用于单元体上，然后用积分形式表示流过单元界面的热量。我们还可以采用更简便的方法，就是从单元体热平衡原理出发，直接写出代数形式的差分方程

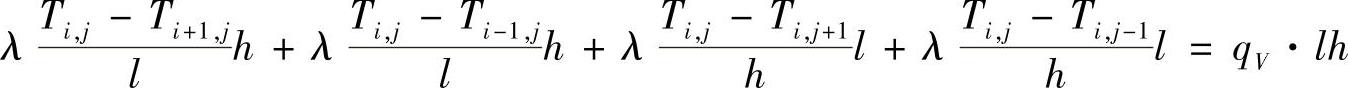
这个对内部单元以代数形式写出的差分方程，经简单整理即可得式（1.3.11）。同样，这种方法也适用边界单元，对于边界单元将在下一节中介绍。

综上所述，用积分恒等式法构成的差分格式，无论从忠实于物理模型方面，还是保证计算精度方面，都比由微分形式出发构成的差分格式更胜一筹。当然，这也不是绝对的，因为由微分形式出发构成的差分格式，在数学上往往更为简捷，更便于计算。