将偏微分方程的每个微商项都用相应的差商代替，写出该偏微分方程在每一个网格结点处对应的差分方程式，则微分方程式化为代数方程组，求解该代数方程组，便得到每个网格结点处变量u（x，y）所对应的u_i，j。下面以典型椭圆型方程为例，介绍有限差分方程的构建。首先，考虑泊松方程

对区域Ω用步长l和h作网格划分，在每一个内点u（x_i，y_j）处用上述有限差分格式将泊松方程离散化，有

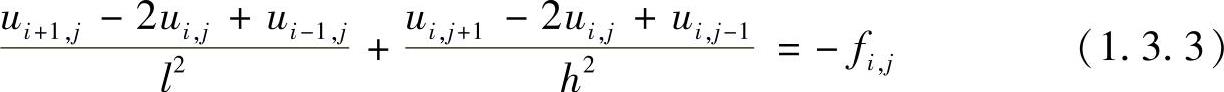
其中，f_i，j=f（x_i，y_j）。式（1.3.3）称为微分方程式（1.3.2）的差分方程或差分格式，u_i，j称为差分解，是u（x_i，y_j）的近似值。可以看到，在差分格式（1.3.3）中只出现内点u（x_i，y_j）及其4个相邻点上u的值。还可以看到，对于正方形网格，即当h=l时，式（1.3.3）变为

4u_i，j-（u_i+1，j+u_i-1，j+u_i，j+1+u_i，j-1）=l²f_i，j （1.3.4）

特别地，对于拉普拉斯方程式（1.1.11），式（1.3.4）变为

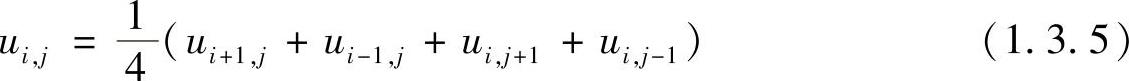
式（1.3.5）表明，u在每一内点处的差分值等于4个相邻结点差分值的算术平均。下面以无内热源的稳态导热问题为例，介绍有限差分方程的构建。

设有一矩形平板，无内热源，其温度场分布满足拉普拉斯方程，设该定解问题为

如图1.3.2所示。

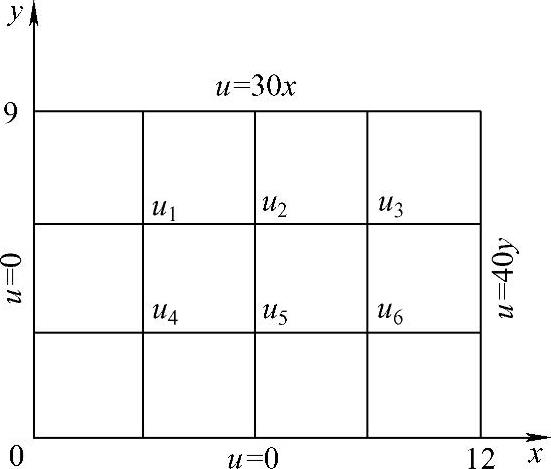
图1.3.2边界条件

取正方形网格l=h=3，由式（1.3.5）得到有限差分方程组

(www.daowen.com)

这是一个线性代数方程组，其矩阵形式为

解之，得

（u₁，u₂，u₃，u₄，u₅，u₆）=（60，120，180，30，60，90）

于是得到温度函数u（x，y）在结点处的近似值。

下面再以典型的抛物型方程均匀细杆的非稳态热传导问题为例，介绍有限差分方程的构建。一维非稳态热传导问题的泛定方程为

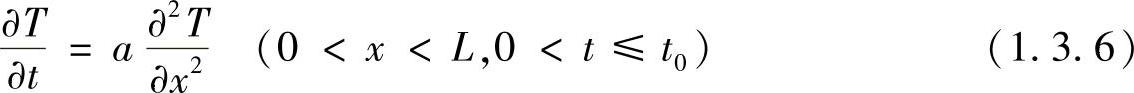
式中，a为导温系数，表示物体在加热或冷却过程中温度趋于均匀一致的能力，设a为常数。

将偏微分方程式（1.3.1）中的偏微分用有限差分表示，为此，用两组平行线x=x_i=il，t=t_n=nτ（i，n=0，1，2，…）作网格划分，得到计算网格如图1.3.3所示。其中，l是沿着x方向将区间[0，L]划分成若干等分，称为空间步长，τ是沿着t方向将区间[0，t₀]划分成若干等分，称为时间步长。x方向离散结点编号用i表示，时间层编号用n表示。将式（1.3.6）中的时间项用前差形式表示，时间差分的截断误差为一阶；二阶空间导数项用中心差分近似，空间差分的截断误差为二阶。略去截断误差，易得

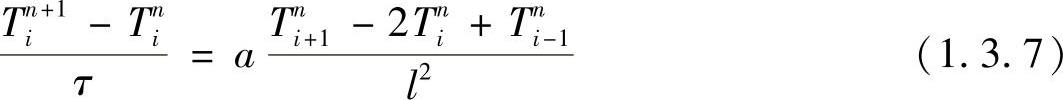
式（1.3.7）就是偏微分方程式（1.3.6）的差分形式，其截断误差为O（τ+l²）。

在图1.3.3中，若对计算域的每个内点均按式（1.3.7）列出，则组成一个代数方程组，通过求解代数方程组可得差分方程在所有网格点上的离散解。应当指出，因计算中存在截断误差和其他误差，网格结点上的差分解并不是偏微分方程真解，而是偏微分方程式（1.3.6）在截断误差之内的近似解。当网格结点数趋于无穷大，即时间步长和空间步长都趋近于零时，差分方程的截断误差也将趋近于零，此时有限差分方程的解趋近于偏微分方程真解。

图1.3.3 计算网格