考虑区域Ω上的二维问题

L[u（x，y）]=f（x，y） （1.3.1）

使其在Ω的边界Γ上满足给定的边界条件，如图1.3.1所示，其中L是微分算子，u=u（x，y）是未知函数。采用有限差分方法求解这个边值问题。

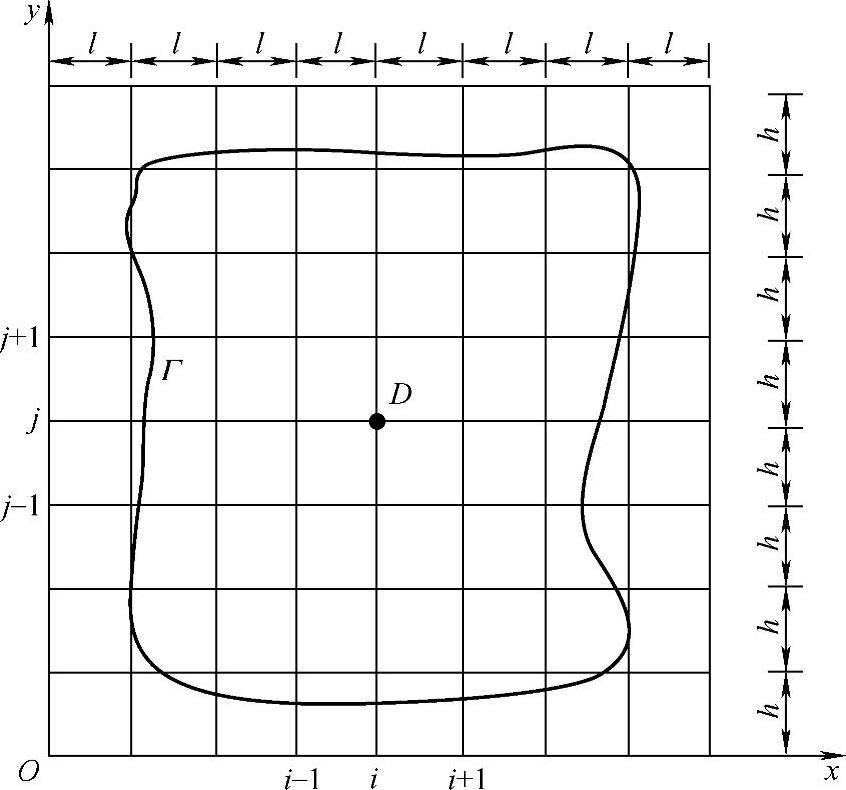
图1.3.1 计算域及其网络划分

与常微分方程的处理方法一样，其基本思想是将偏微分方程离散化，即用差商代替偏导数，把偏微分方程边值问题转化为代数方程问题，然后求解所得的代数方程组。

在xOy平面上作两组平行线，使得

x=x_i=il，y=y_j=jh（i，j=0，±1，±2，…）

这样就得到矩形网格。其中，l＞0和h＞0称为步长；网格线的交点（x_i，y_j）称为结点。通常把结点（x_i，y_j）简记为（i，j）。我们只关心属于Ω=D+Γ的结点，若两个结点沿着坐标轴方向只相差一个步长，则称这两个结点为相邻结点。若一个属于Ω的结点，其4个相邻结点都属于Ω，则称此结点为内点，若4个相邻结点中至少有一个不属于Ω，则称此结点为边界点。

以上构造了网格，在此基础上，需要偏微分方程离散化，将偏导数以有限差商的形式表示。对变量x的偏导数

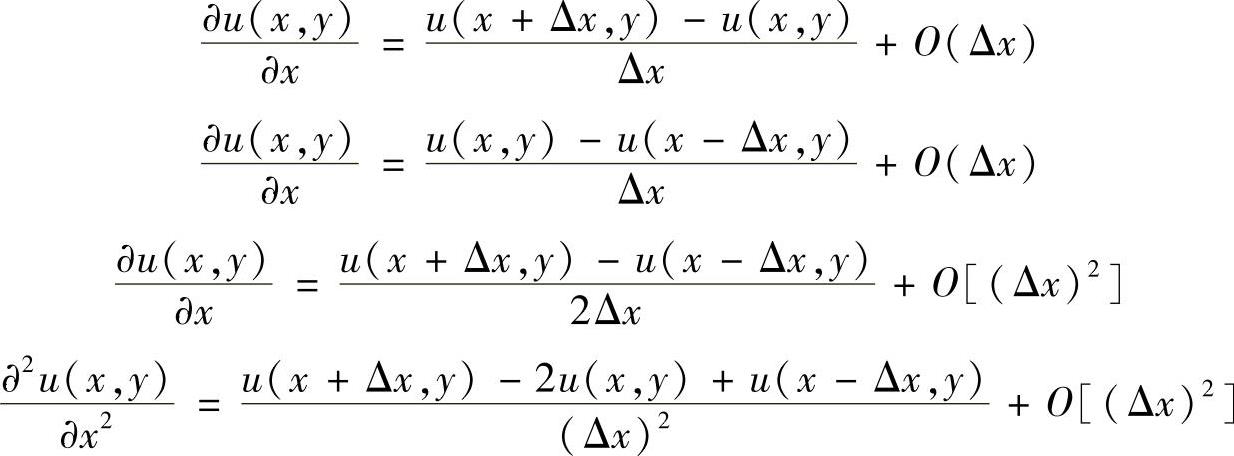(www.daowen.com)

以及对变量y的偏导数

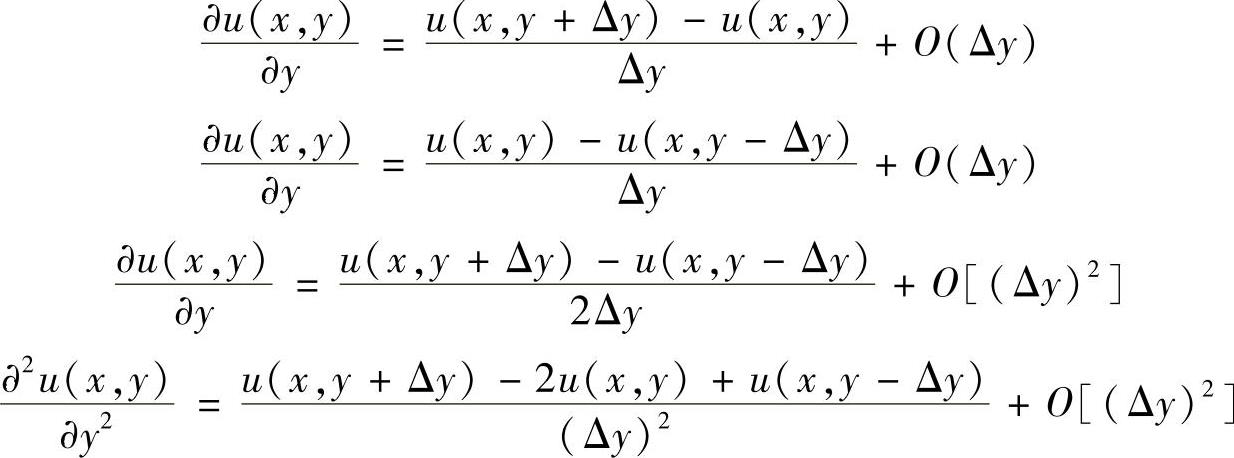
若将空间点（i，j）的变量写成u_i，j，将空间点（i+1，j）的变量写成u_i+1，j，等等，则可在x方向上对点（i，j）的邻域进行Taylor展开，不难得到

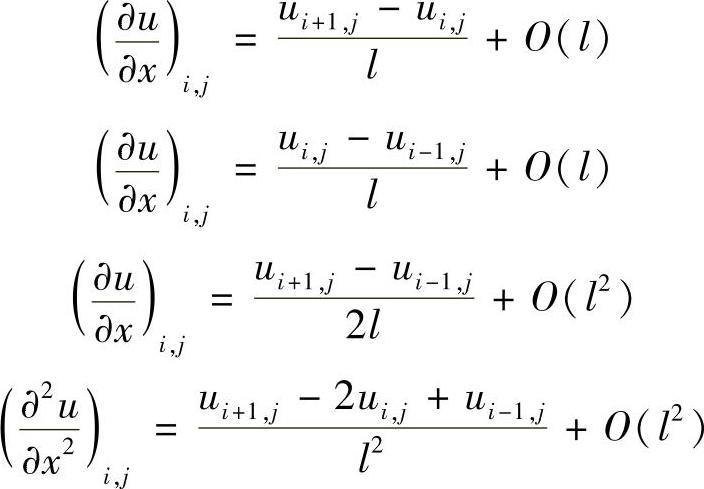
用同样的方法可得微商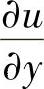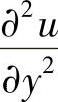，以及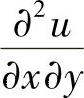相对应的差分式及其截断误差，即

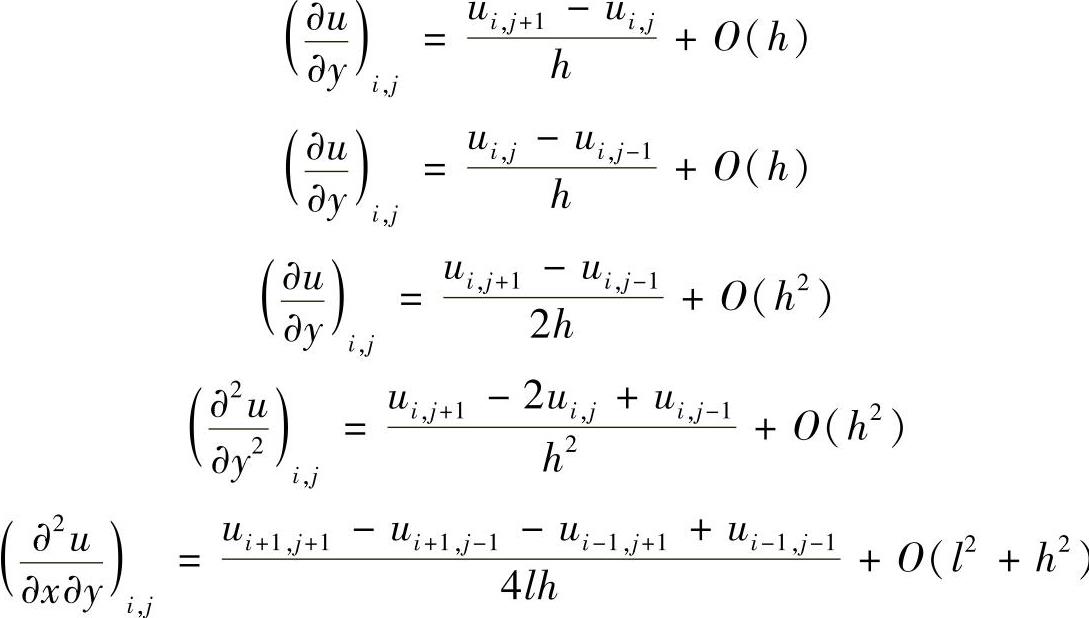
若偏微分方程中含有时间偏导数项，类似于上述对空间偏导数的处理方式，不难写出相应的差分格式。例如，采用前差格式和中心差分格式，有

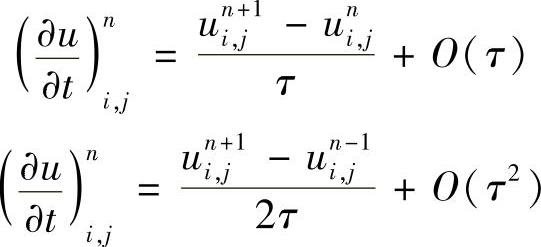
其中，τ=Δt，为时间步长，上标n表示时间t=nΔt。