我们回顾线性代数的相关理论，要证明一个线性代数方程组解的存在且唯一，只需证明其对应的齐次方程组只有零解，此即克莱姆（Cramer）法则。若n元非齐次线性方程组

的系数行列式

则该n元非齐次线性方程组有唯一解，且可表示为

x₁=D₁ /D，x₂=D₂/D，…，x_j=D_j/D，…，x_n=D_n/D

其中，

克莱姆法则的结论包含三方面内容，①方程组有解；②解唯一；③解的表达式。根据克莱姆法则还可以得出，若方程个数等于未知数个数的齐次线性方程组有非零解，则其系数行列式D=0。

我们应当注意克莱姆法则的适用的条件，即①方程组中方程的个数必须等于未知量的个数，否则不能形成系数行列式；②系数行列式D≠0。这两个条件中的任何一个不具备都不能应用克莱姆法则。由此可见，当需要对一般的非齐次线性方程组的解作定性研究时，克莱姆法则具有重要作用。

在差分方程式（1.2.20）中，将y₀和y_N消去，可以得到一个N-1阶三对角的线性方程组

为了研究方程式（1.2.21）解的存在性和唯一性，需引入极值原理。

定理（极值原理）设给定一组数y₀，y₁，y₂，…，y_N，满足条件

l（y_j）=a_jy_j-1+b_jy_j+c_jy_j+1≤0（j=1，2，…，N-1）其中，l为算子；a_j＜0，b_j＞0，c_j＜0，且|b_j|≥|a_j|+|c_j|。若所有y_j不全相等，则这组数中正的最大值只能在y₀或y_N上达到。

证明用反证法，假设

在y₁，y₂，…，y_N-1中达到最大值，因所有y_j不全相等，故总存在某个自然数k（1≤k≤N-1），使y_k=M，而y_k-1和y_k+1中至少有一个小于M。(www.daowen.com)

令λ_k=-a_k/b_k＞0，μ_k=-c_k/b_k＞0，则0＜λ_k+μ_k≤1，于是

l（y_k）=a_ky_k-1+b_ky_k+c_ky_k+1=b_k（y_k-λ_ky_k-1-μ_ky_k+1）

=b_k[M-（λ_ky_k-1+μ_ky_k+1）]＞b_k（M-M）=0

这与假设矛盾，故原定理得证。

类似地可以证明，若l（y_j）≥0（j=1，2，…，N-1），且所有y_j不全相等，则这组数中负的最小值只能在y₀或y_N上达到。

定理推论 设p（x），q（x）和r（x）在[a，b]上连续，且q（x）≥0。记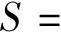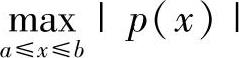，若步长h满足条件

hS＜2

即h足够小，则差分方程组式（1.2.20）的解存在且唯一。

证明 差分方程组式（1.2.20）所对应的齐次方程组是

由假设条件，得

而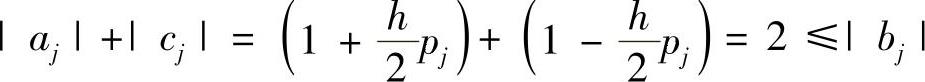即a_j，b_j和c_j满足极值定理的条件。因此，根据极值定理，对于齐次方程组的解{y_j}，其正的最大值和负的最小值只能是y₀或y_N，而现在y₀=y_N=0，故y_j=0（j=0，1，2，…，N），即差分方程组式（1.2.20）解存在且唯一。