线性常微分方程边值问题的有限差分法求解：土建类书籍

考虑二阶线性常微分方程和边界条件

其中，p（x），q（x）和r（x）都是在[a，b]上已知的连续函数，且q（x）＞0，α和β为已知常数。以下我们来建立差分方程。将区间[a，b]分成N等分，结点为

x_j=a+jh（j=0，1，2，…，N）其中，h=（b-a）/N为步长，点x₁，x₂，…，x_N-1称为内结点，x₀和x_N称为边界结点。

在每一内结点x_j处，利用导数y″和y′的有限差分公式，代入方程式（1.2.17），得

如果引入差分算子L_h，使

其中，x为[a，b]的内结点，则式（1.2.18）可表示为

L_h[y（x_j）]+O（h²）=r（x_j）(https://www.daowen.com)

显然，若h足够小，则可忽略O（h²），而得差分方程

其中，p_j=p（x_j），q_j=q（x_j），r_j=r（x_j）。

于是，常微分方程边值问题，即式（1.2.17）可近似地表达为

其中，，，。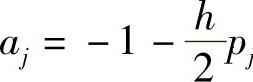

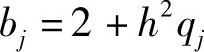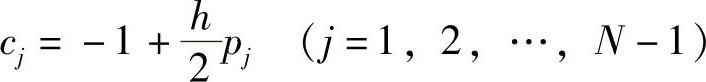式（1.2.20）称为逼近常微分方程边值问题式（1.2.17）的差分方程，式（1.2.20）的解称为差分解，该差分解是边值问题式（1.2.17）的解函数y（x）在结点x_j（j=0，1，2，…，N）处的近似值，即y_j=y（x_j）。

以上通过有限差分处理，将常微分方程边值问题转化为差分方程。事实上，对于差分方程，我们还必须知道差分方程的存在性、唯一性和收敛性。