6.6.1.1　关键路径法

关键路径法是在进度模型中，估算项目最短工期并确定逻辑网络路径的进度灵活性大小的一种网络图技术。这种进度网络分析技术在不考虑任何资源限制的情况下，沿进度网络路径顺推与逆推分析，计算出所有活动的最早开始、最早结束、最晚开始和最晚结束日期。

关键路径法属于一种数学分析方法，包括理论上计算所有活动各自的最早、最晚开始日期与结束日期。讲述关键路径进度编排方法前，先来了解一下有关进度编制的基本术语。

1．最早开始时间（Early Start，ES）

表示一项任务（活动）的最早可以开始执行的时间。

2．最晚开始时间（Late Start，LS）

表示一项任务（活动）的最晚可以开始执行的时间。

3．最早完成时间（Early Finish，EF）

表示一项任务（活动）的最早可以完成的时间。

4．最晚完成时间（Late Finish，LF）

表示一项任务（活动）的最晚可以完成的时间。

5．超前（lead）

表示两个任务（活动）的逻辑关系所允许的提前后置任务（活动）的时间，它是网络图中活动间的固定可提前时间。

6．滞后（lag）

表示两个任务间或网络图中活动间的固定等待时间。举一个简单的例子：装修房子的时候，需要粉刷房子，刷油漆的后续活动是刷涂料，它们之间需要至少一段时间（一般是一天）的等待时间，等油漆变干后，再刷涂料，这个等待时间就是滞后。

7．浮动时间

浮动时间是一个任务（活动）的机动性，它是一个活动在不影响项目完成的情况下可以延迟的时间量。

（1）总浮动（Total Float，TF）：在不影响项目最早完成时间的前提下，本任务（活动）可以延迟的时间。TF＝LS－ES或者TF＝LF－EF。

（2）自由浮动（Free Float，FF）：在不影响后置任务最早开始时间的前提下，本任务（活动）可以延迟的时间。某任务的自由浮动FF＝ES（successor）－EF－lag（successor表示后置任务，lag 是本任务与后置任务之间的滞后时间），即某任务的自由浮动等于它后置任务的ES减去它的EF，再减去它的lag。自由浮动是对总浮动的描述，表明总浮动的自由度。

8．关键路径

项目是由各个任务构成的，每个任务都有一个最早、最迟的开始时间和结束时间，如果一个任务的最早时间和最迟时间相同，则表示其为关键任务，一系列不同任务链条上的关键任务链接成为项目的关键路径。关键路径是整个项目的主要矛盾，是确保项目能否按时完成的关键。关键路径在网络图中的浮动为0，而且是网络图中的最长路径。关键路径上的任何活动延迟都会导致整个项目完成时间的延迟，它是完成项目的最短时间量。

下面以图6-6为例来进一步说明以上基本术语的含义（假设所有任务的历时以天为单位）。

图6-6　项目网络图

在图6-6中，A、B、C是并行的关系，则项目的完成时间是100。任务A的最早开始时间和早晚开始时间都为0，最早结束时间和最晚结束时间都为100，所以ES（A）＝0，EF（A）＝100，LF（A）＝100，LS（A）＝0。

任务B的历时为10天，所以可以有一定的浮动时间，只要在任务A完成之前完成任务B就可以了，所以，任务B的最早开始时间是0，最早结束时间是10；而最晚结束时间是100，最晚开始时间是90，可知任务B有90天的浮动时间，这个浮动是总浮动。总浮动是在不影响项目最早完成时间本活动可以延迟的时间，任务B的总浮动＝90－0＝100－10＝90。所以ES（B）＝0，EF（B）＝10，LF（B）＝100，LS（B）＝90，TF（B）＝LS（B）－ES（B）＝LF（B）－EF（B）＝90。

任务C是任务D的前置任务，任务D是任务C的后置任务，它们之间的lag＝5表示任务C完成后的5天开始执行任务D。C任务的历时是10，D任务的历时是5，所以任务C和任务D的最早开始时间分别是0和15，最早结束时间分别是10和20，如果保证任务D的最早开始时间不受影响，任务C是不能自由浮动的，所以任务C的自由浮动为0，即FF（C）＝ES（D）－EF（C）－lag＝0，其中ES（D）是任务D的最早开始时间，EF（C）是任务C的最早完成时间。任务D的最晚结束时间是100，则任务D的最晚开始时间是95，这样，任务C的最晚结束时间是90，任务C的最晚开始时间是80。所以ES（C）＝0，EF（C）＝10，ES（D）＝15，EF（D）＝20，LF（D）＝100，LS（D）＝95，LF（C）＝90，LS（C）＝80，TF（C）＝LS（B）－ES（B）＝LF（B）－EF（B）＝80，FF（C）＝ES（D）－EF（C）－lag＝0。

从图6-6中可以看出，路径A是浮动为0且是网络图中的最长路径，所以它是关键路径，是完成项目的最短时间。下面再看图6-7是如何确定其中的关键路径的（假设所有任务的历时以天为单位）：

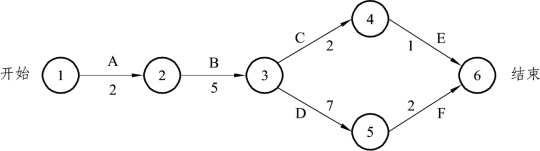
图6-7　项目网络图

（1）从网络图可以知道有两条路径：A→B→C→E和A→B→D→F。

（2）A→B→C→E的长度是10，有浮动时间；A→B→D→F的长度是16，没有浮动时间。

（3）最长而且没有浮动的路径A→B→D→F便是关键路径。

（4）项目完成的最短时间是16天，即关键路径的长度是16天。图6-8所示代表网络图中的一个任务（活动），其中，图中标识出任务的名称、工期，同时可以标识出任务的最早开始时间（ES）、最早完成时间（EF）、最晚开始时间（LS）以及最晚完成时间（LF）。为了能够确定项目路径中各个任务的最早开始时间、最早完成时间、最晚开始时间、最晚完成时间，可以采用正推法和逆推法来确定。

图6-8　任务图示

① 正推法。

在网络图中按照时间顺序计算各个任务（活动）的最早开始时间和最早完成时间的方法称为正推法。此方法的执行过程如下：

a.确定项目的开始时间。

b.从左到右，从上到下进行任务编排。

c.计算每个任务的最早开始时间ES和最早完成时间EF：

网络图中第一个任务的最早开始时间是项目的开始时间；

ES＋Duration＝EF：任务的最早完成时间等于它的最早开始时间与任务的历时之和，其中Duration是任务的历时时间；

EF＋lag＝ES（s）：任务的最早完成时间加上（它与后置任务的）lag等于后置任务的最早开始时间，其中ES（s）是后置任务的最早开始时间；

当一个任务有多个前置任务时，选择前置任务中最大的EF加上lag（或者减lead）作为其ES。

图6-9所示网络图（假设所有任务的历时以天为单位）中项目的开始时间是1。如任务A，它的最早开始时间ES（A）＝1，任务历时Duration＝7，则任务A的最早完成时间是EF（A）＝1＋7＝8。同理可以计算EF（B）＝1＋3＝4。任务C的最早开始时间ES（C）＝EF（A）＋0＝8，最早完成时间是EF（C）＝8＋6＝14。任务G的最早开始时间和最早完成时间ES（G）＝14，EF（G）＝14＋3＝17。同理ES（D）＝4，EF（D）＝7，ES（F）＝4，EF（F）＝6。由于任务E有两个前置任务，选择其中最大的最早完成日期（因为lag＝0，lead＝0）作为其后置任务的最早开始日期，所以ES（E）＝7，EF（E）＝10。任务H也有两个前置：任务E和任务G，选择其中最大的最早完成时间17（因为lag＝0，lead＝0），作为任务H的最早开始时间EF（H）＝17，EF（H）＝19。

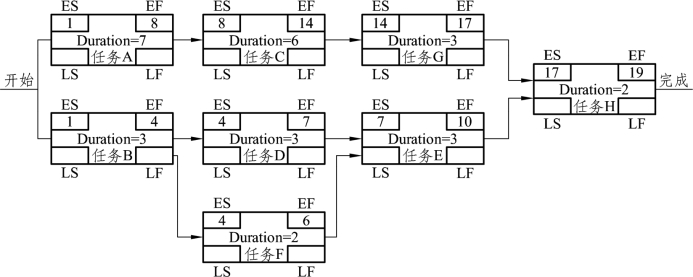
图6-9　正推法

这样，通过正推法确定了网络图中各个任务（活动）的最早开始时间和最早完成时间。

② 逆推法。

在网络图中按照逆时间顺序计算各个任务（活动）的最晚开始时间和最晚完成时间的方法，称为逆推法。此方法的执行过程如下：

a.确定项目的结束时间。

b.从右到左，从上到下进行任务编排。

c.计算每个任务的最晚开始时间LS和最晚完成时间LF：

网络图中最后一个任务的最晚完成时间是项目的结束时间；

LF－Duration＝LS：一个任务的最晚开始时间等于它的最晚完成时间与历时之差；

LS－Lag＝LF（p）：一个任务的最晚开始与（它与其前置任务的）lag之差等于它的前置任务的最晚完成时间LF（p），其中LF（p）是其前置任务的最晚完成时间；

当一个任务有多个后置任务时，选择其后置任务中最小LS减lag（或者加上lead）作为其LF。

下面确定图6-10中各个任务（活动）的最晚开始时间和最晚完成时间。由于项目的结束时间是网络图中最后一个任务（活动）的最晚开始时间，对于图6-10所示网络图，这个项目的结束时间是19，即LF（H）＝19，则LS（H）＝19－2＝17，LF（E）＝17，LS（E）＝17－3＝14。同理，任务G、C、A、D、F最晚完成和最晚开始时间分别如下：LF（G）＝17，LS（G）＝17－3＝14；LF（C）＝14，LS（C）＝14－6＝8；LF（A）＝8，LS（A）＝8－7＝1；LF（D）＝14，LS（D）＝14－3＝11； LF（F）＝14，LS（F）＝14－2＝12。任务B有两个后置任务，选择其中最小最晚开始日期（因为lag＝0，lead＝0）作为其前置任务的最晚完成日期，所以11作为任务B的最晚完成日期，即LF（B）＝11，LS（B）＝11－3＝8。另外，对于任务F，它的自由浮动时间是1［FF（F）＝7－6］；而它的总浮动时间是8［TF（F）＝12－4＝8］。结果如图6-10所示，图中A→C→G→H的浮动为0，而且是最长的路径，所以它是关键路径。关键路径长度是19，所以项目的完成时间是19天，并且A、C、G、H都是关键任务。(www.daowen.com)

图6-10所示网络图可以称为CPM网络图，如果采用PERT进行历时估计，则可以称为PERT网络图。PERT网络与CPM网络是20世纪50年代末发展起来的两项重要的技术，其主要区别是PERT计算历时时存在一定的不确定性，采用的算法是加权平均（0＋4M＋P）/6，CPM计算历时的意见比较统一，采用的算法是最大可能M，1956年美国杜邦公司首先在化学工业上使用CPM（关键路径法）进行计划编排，美国海军在建立北极星导弹时，采用了Buzllen提出的PERT（计划评审法）技术。这两种方法才逐渐渗透到许多领域，为越来越多的人所采用，成为网络计划技术的主流。网络计划技术作为现代管理的方法与传统的计划管理方法相比较，具有明显优点，主要表现为：

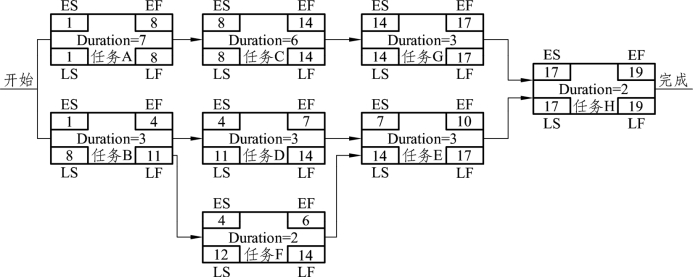
图6-10　逆推法

（1）利用网络图模型，明确表达各项工作的逻辑关系。按照网络计划方法，在制订工程计划时，首先必须清楚该项目内的全部工作和它们之间的相互关系，然后才能绘制网络图模型。

（2）通过网络图时间参数计算，确定关键工作和关键线路。

（3）掌握机动时间，进行资源合理分配。

（4）运用计算机辅助手段，方便网络计划的调整与控制。

我国从20世纪60年代中期开始，在著名数学家华罗庚教授的倡导和亲自指导下开始试点应用网络计划，并根据“统筹方法，全面安排”的指导思想，将这种方法命名为“统筹方法”网络计划技术，从此该方法在国内生产建设中卓有成效地推广开来。

为确保网络图的完整和安排的合理，可以进行如下检查：

（1）是否正确标识了关键路径？

（2）是否有哪个任务存在很大的浮动？如果有，则需要重新规划。

（3）是否有不合理的空闲时间？

（4）关键路径上有什么风险？

（5）浮动有多大？

（6）哪些任务有哪种类型的浮动？

（7）工作可以在期望的时间内完成吗？

（8）提交物可以在规定的时间内完成吗？

关键路径法是理论上计算所有活动各自的最早和最晚开始日期与结束日期，但计算时并没有考虑资源限制，这样算出的日期可能并不是实际进度，而是表示所需的时间长短，在编排实际的进度时，应该考虑资源限制和其他约束条件，把活动安排在上述时间区间内，所以还需要如时间压缩、资源调整等方法。

6.6.1.2　甘特图

甘特（Gantt）图历史悠久，具有直观简明、容易学习、容易绘制等优点。甘特图可以显示任务的基本信息。使用甘特图能方便地查看任务的工期、开始和结束时间以及资源的信息。甘特图有两种表示方法，这两种方法都是将任务（工作）分解结构中的任务排列在垂直轴，而水平轴表示时间。一种是棒状图（Bar Chart），用于表示任务的起止时间，如图6-11所示。空心棒状图表示计划起止时间，实心棒状图表示实际起止时间。用棒状图表示任务进度时，一个任务需要占用两行的空间。另外一种表示甘特图的方式如图6-12所示，是用三角形表示特定日期。向上三角形表示开始时间，向下三角形表示结束时间，计划时间和实际时间分别用空心三角和实心三角表示。一个任务只需要占用一行的空间。

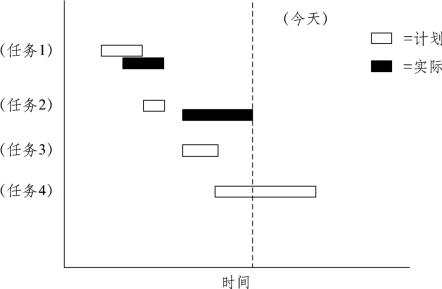
图6-11　棒状图

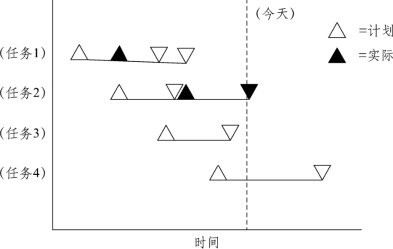
图6-12　三角形甘特图

这两个图示说明同样的问题，从图中可以看出所有任务的起止时间都比计划推迟了，而且任务2的历时也比计划长很多。

甘特图可以很容易看出一个任务的开始时间和结束时间，简单、明了、直观、易于编制，因此到目前为止仍然是小型项目中常用的工具。但是不能系统地表达一个项目所包含的各项工作之间的复杂关系，难以进行定量的计算和分析，以及计划的优化，同时也没有指出影响项目寿命周期的关键所在。

6.6.1.3　关键链法

关键链法（CCM）是一种进度规划方法，允许项目团队在任何项目进度路径上设置缓冲，以应对资源限制和项目不确定性。这种方法建立在关键路径法之上，考虑了资源分配、资源优化、资源平衡和活动历时不确定性对关键路径（通过关键路径法来确定）的影响。关键链法引入了缓冲和缓冲管理的概念。在关键链法中，也需要考虑活动持续时间、逻辑关系和资源可用性，其中活动持续时间中不包含安全冗余。它用统计方法确定缓冲时段，作为各活动的集中安全冗余，放置在项目进度路径的特定节点，用来应对资源限制和项目不确定性。资源约束型关键路径就是关键链。

关键链法增加了作为“非工作进度活动”的持续时间缓冲，用来应对不确定性，项目缓冲放置在关键链末端的缓冲，用来保证项目不因关键链的延误而延误。

其他的缓冲，即接驳缓冲，则放置在非关键链与关键链的接合点，用来保护关键链不受非关键链延误的影响，如图6-13所示。

图6-13　关键链图

6.6.1.4　工程评估评审技术

工程评估评审技术（Program Evaluation and Review Technique，PERT）最初发展于1958年，用来适应大型工程年代的需要。当时由于美国海军专门项目处关心大型军事项目的发展计划，于1958年将PERT引入海军北极星导弹开发项目中，取得不错的效果。PERT是利用网络顺序图的逻辑关系和加权历时估算来计算项目历时的。当估计历时存在不确定性时，可以采用PERT方法，即估计其有一定的风险时采用这种方法。PERT方法采用加权平均的算法进行历时估算。

PERT历时＝（O＋4M＋P）/6，其中O是活动（项）完成的最小估算值，或者说是最乐观值（Optimistic Time）；P是活动（项目）完成的最大估算值，或者说是最悲观值（Pessimistic Time）；M是活动（项目）完成的最大可能估算值（Most Likely Time）。最乐观值是基于最好情况的估计，最悲观值是基于最差情况的估计，最大可能估算值是基于最大可能情况的估计或者基于最期望情况的估计。在图6-14的网络图中，估计A、B、C任务的历时存在很大不确定性，故采用PERT方法估计任务历时，图6-14中标示了A、B、C任务的最乐观、最可能和最悲观的历时估计，根据PERT历时公式，计算各个任务的历时估计结果，见表6-6。

图6-14　ADM网络图

一个路径上的所有活动（任务）的历时估计之和便是这个路径的历时估计，其值称为路径长度。图6-14中的路径长度为13.5，即这个项目总的时间估计是13.5，见表6-6。

表6-6　PERT方法估计项目历时

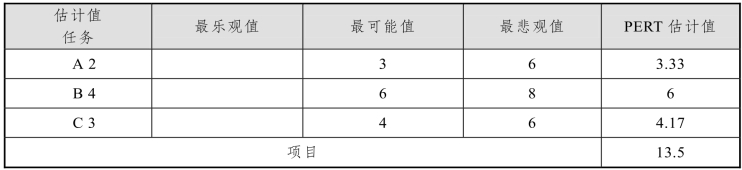
用PERT方法估计历时存在一定的风险，因此有必要进一步给出风险分析结果。为此引入了标准差（Standard Deviation）和方差（Variance）的概念。

标准差

方差

式中，O是最乐观的估计；P是最悲观的估计。标准差和方差可以表示历时估计的可信度或者项目完成的概率。如果需要估计网络图中一条路径的历时情况，一个路径中每个活动的PERT历时估计分别为E1,E2,…,En，标准差分别为δ1,δ2,…,δn，则这个路径的历时、方差、标准差分别如下

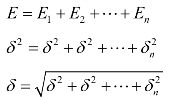
图6-15中A、B、C任务的标准差和方差以及这个路径的标准差和方差如表6-7所示。

表6-7　项目的标准差和方差

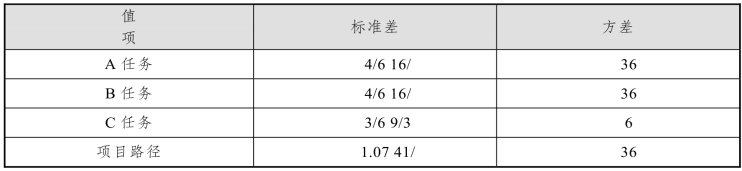
根据概率理论，计算出表6-8所示结果。对于遵循正态概率分布的均值E而言，E±δ的概率分布是68.3%，E±2δ的概率分布是95.5%，E±3δ的概率分布是99.7%，如图6-15所示。标准差δ＝1.07。这个项目总历时估计的如表6-8所示，项目的PERT总历时估计是13.5天，项目在12.43天14.57天内完成的概率是68.3%，项目在11.36天到15.64天内完成的概率是95.5%，项目在10.29天到16.71天内完成的概率是99.7%。

图6-15　正态概率分布

表6-8　项目完成的概率分布

图6-16所示为项目在14.57天内完成的概率。由于14.57＝13.5＋1.07＝E+δ，因此项目在14.57天内完成的概率是箭头1以左的概率，很显然它等于箭头2以左的概率加上68.3/2，即84.2%，所以项目在14.57天内完成的概率是84.2%，即接近85%。

图6-16　项目在14.57天内完成的概率