有两个木槌球，一个放在原地不动，另一个撞击这个静止不动的木槌球，此时就会形成力学上的“正碰”与“对心碰”现象。这种撞击的碰撞方向和通过碰撞施力点的球的直径方向重合。

请问，这两个球在相撞后会怎么样？

假如这两个木槌球的质量相同，而且都是“完全没有弹性”的，那么它们相撞后的速度也相同，都与撞过去的那个球的速度的一半相等。从公式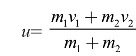中能够得出这个结论。式子中，m1=m2，v2=0。

反过来，假如两个木槌球都是“完全有弹性”的，那么我们就可以下这样的结论：两个木槌球会互换速度，即撞过去的木槌球会停止运动，原本固定不动的木槌球却沿碰撞的方向进行运动，速度则和撞过来的木槌球的速度相同。对此，读者朋友们只要演算一下，很容易就能证实。打弹子球的时候，两个弹子球互相碰撞后便经常会有这样的情况发生。一般来说，这种弹子球往往是用象牙做的，而象牙的恢复系数e比较大，大约是。

可是在通常情况下，木槌球的恢复系数小得多，仅为0.5，所以最终的碰撞结果就不一样了。两个木槌球会一块运动，运动的速度却不一样。撞过去的木槌球的速度小于被撞的木槌球的速度。详细的情形，我们可以根据物体碰撞的公式进行分析。

假设木槌球的恢复系数是e。我们已经得出了两个木槌球碰撞之后的速度u1与u2的计算公式，它们分别为：

u1=(1+e)u-ev1

u2=(1+e)u-ev2(www.daowen.com)

我们还知道

我们已经知道m1=m2，v2=0。代入上面的式子，可以得出

将公式变化，可以得出

u2-u1=ev1

由此，我们便能精准地对木槌球相撞之后的情形进行描述。撞过去的木槌球将它的速度在两个木槌球之间重新进行了分配，被撞的木槌球得到的速度比撞过来的木槌球的最终速度大。准确来说，这两个木槌球速度的差和撞过来的木槌球原本速度的e倍相等，即u2-u1=ev1。

举例来讲，假设e=0.5，那么原本静止不动的木槌球得到的速度就是撞过来的木槌球的原本速度的，撞过来的木槌球的速度则会变成原本速度的，因此落在后边的木槌球是撞过去的木槌球。