以往的研究者大多仅从各个检验指标（如R2、F统计量等）判断模型的优劣，只有Shahriari ＆ Frost（2008）通过将模型与实际已发生的溢油事故进行比较来判断其所得模型的优劣，但Shahriari ＆ Frost是通过散点图进行分析的，其分析较粗糙。本节通过对上一节计算的模型偏离度的分析，可以更加清晰地判断各个模型的优劣。具体做法是，通过分析各模型的计算结果落在限定偏离度区间内的个数来判断模型对海上溢油生态损害经济补偿估计的精确度，分析结果如表6- 5。

表6-5　各模型计算结果落在限定偏离度区域的个数

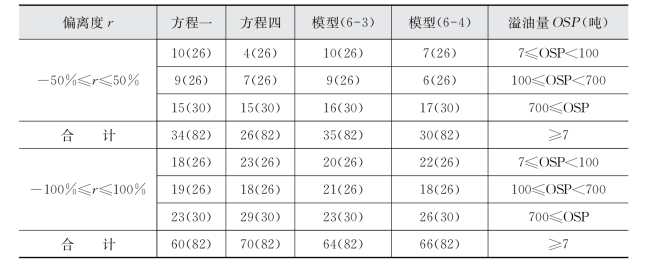
注：括号中的数字为样本数。(www.daowen.com)

表6-5表明，相比于中型溢油事故，模型对大型溢油事故补偿额的估计要精确得多，当偏离度限定在［－50%，50%］时，无论方程一还是方程四，其估计结果与实际补偿额相近的比例都超过50%；一旦将偏离度放宽到［－100%，100%］，该比例便提高到80%左右。相比于方程一，方程四对补偿额的估计更加接近实际情况，并且从附表四中的结果也可以看出，方程四的计算结果表现出更强的规律性，即落在偏离度为［－100%，100%］区间的70个计算结果中，有56个结果为负数，而方程一的60个结果中，仅有40个结果为负数。鉴于IOPC Funds处理溢油事故的实践及各国处理该类事故的惯例，本书倾向于使用方程四及其误差修正模型作为衡量海上溢油生态损害经济补偿的模型，将方程一及其误差修正模型作为备用模型，即

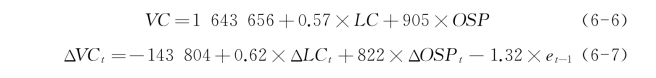
在实践中，海上溢油生态损害经济补偿通常以整数形式出现，因此，为了计算方便，本书将常数保留为整数，当系数小于零时保留2位小数，系数大于零时保留整数。