附表三的数据表明，无论是补偿额还是责任限额和溢油量数据都不是严格规范的时间序列数据或者横截数据，因此，为了提高计量结果的可信度，需要对数据及计量结果进行必要的检验。

1.数据平稳性。

在涉及时间序列数据时，数据的平稳性对回归方程非常重要。如果数据是非平稳的，直接对数据进行回归分析会导致“伪回归”问题，为了避免此问题，本书首先使用eview 6.0对数据的平稳性进行检验，检验结果如表6- 1。

表6-1　因变量与自变量平稳性检验（ADF单位根检验）

注：检验为含有常数项和趋势项的水平检验。

表6-1表明，对数据无论是否取对数，数据都在1%的显著性水平上拒绝原假设（H0：数据存在单位根），数据是平稳的，因此，数据都是0阶单整的。2.格兰杰因果关系检验。

尽管数据是平稳的，但需要进一步检验自变量与因变量之间是否存在因果关系。格兰杰（Granger）因果关系检验结果如表6- 2。

表6-2　格兰杰因果关系检验

注：滞后期为2。

表6-2表明，在没有取对数的情况下，拒绝“责任限额不是补偿额的格兰杰原因”犯第一类错误的概率为0.418 6，小于0.5，但如果拒绝“补偿额不是责任限额的格兰杰原因”犯第一类错误的概率则为0.914 8，远远大于0.5，因此，可以拒绝原假设，而认为责任限额是补偿额的格兰杰原因。同样，溢油量也是补偿额的格兰杰原因。因此，在线性回归分析中，因变量和自变量之间存在因果关系。在取对数之后，责任限额的对数可以勉强称为补偿额对数的格兰杰原因，但溢油量的对数却不是补偿额对数的格兰杰的原因。

3.协整检验。

在寻找变量间关系时，研究者通常使用协整方程来确定变量之间的长期关系，并通过各检验指标来判断所得到模型的可信度，如R2、F统计量、t统计量、杜宾-沃森检验（DW检验）等。如Kontovas et al.（2011）提到的美国早期开展的基于美国溢油责任信托基金（Oil Spill Liabilty Trust Fund，简称OSLTF）数据关于清污成本与溢油量关系的回归分析，其R2最大仅为0.240 5，作者据此便认为其回归方程的拟合度低^[3]，并致力于新模型的构建，以便为实际提供更具有说服力的模型。在诸多检验指标中，R2、F统计量、杜宾-沃森检验（DW检验）通常被用来作为判断各协整方程可信度高低的指标。本书通过逐步回归法所得到的因变量与自变量间的协整方程及各检验指标结果如表6- 3所示。

表6-3　协整方程及各检验量

(www.daowen.com)

注：方程中的数值保留到小数点后4位。

从表6-3可以看出，在对数关系中，方程一的拟合度要优于方程二和方程三，自相关的可能性要小于方程二和方程三。而在线性关系中，方程四基本上从各个方面都要优于方程五和方程六。因此，只要方程一与方程四真正存在协整关系，就可以使用这两个方程作为表示海上溢油生态损害经济补偿与责任限额、溢油量之间关系的方程。但方程之间是否真正存在协整关系，还需要进一步对其进行协整检验。如果通过协整检验，则说明方程之间存在协整关系，否则，方程之间则不存在协整关系。基于以上分析，本书首先对方程一和方程四进行协整检验，如果这两个方程无法通过协整检验，再分别对其他四个方程进行协整检验，以便确定因变量和自变量之间的协整关系。本书采用恩格尔-格兰杰检验（EG两步法），通过对残差的平稳性进行检验来确定因变量与自变量之间是否存在协整关系。令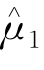、分别是方程一和方程四的残差，其平稳性检验如表6- 4。

表6-4　残差项的平稳性检验（ADF单位根检验）

注：检验为含有常数项和趋势项的水平检验。

表6-4表明，方程一和方程四的残差都是平稳的，即因变量（补偿额）和自变量（责任限额和溢油量）之间存在着协整关系。那么，使用方程一与方程四测算海上溢油生态损害经济补偿额的长期发展趋势是合理的。

4.误差修正模型。

协整关系表明变量之间存在长期均衡关系，但作为一种趋势的长期均衡，无法反应短期波动。误差修正模型（ECM模型）弥补了协整关系的不足，能够提高预测的精度。基于补偿额、责任限额和溢油量之间存在协整关系，为了提高预测精确度，本书分别对方程一和方程四进行误差修正，建立误差修正模型如下：

（1）方程一的误差修正模型。

上式括号中的为t统计量，调整后的R2＝0.808 482。

（2）方程四的误差修正模型。

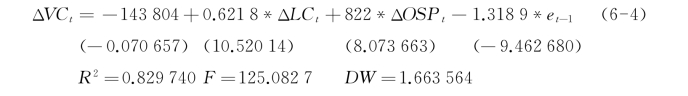
上式括号中的为t统计量，调整后的R2＝0.823 106。

从协整关系的各检验量看，方程一要优于方程四，即在长期中，对数线性关系更能刻画补偿额、责任限额和溢油量之间的关系；但在误差修正模型中，方程四的误差修正模型的大部分检验指标都优于方程一的误差修正模型，即短期中，方程四的误差修正模型能够更好地拟合补偿额、责任限额和溢油量之间的关系。故很难区分哪一个模型更加适用于预测海上溢油生态损害经济补偿。因此，需要分别对两个模型进行检测和甄别，以甄选出最优的海上溢油生态损害经济补偿、责任限额和溢油量之间的回归方程。