1.响应面法概述

响应面法中可以选择三种方法:中心合成设计、Box-Behnken矩阵法和用户指定法。

响应面法假设随机输入变量对于随机输出变量的影响可以用数学函数来表达。因此，响应面法在随机输入变量空间中定位采样点，使得近似函数最有效:通常，函数是一个二次多项式，那么拟合函数可以表示为:

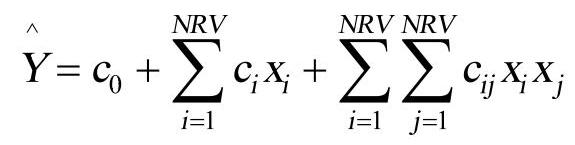
其中，c₀为常数项，c_i、i=1LNRV为线性项系数，c_ij,j=1LNRV,j=iLNRV为二次项系数。为得到这些系数要使用回归分析，通常是用最小二乘法来确定。

因此，响应面法包含两个步骤：

1）进行仿真循环计算对应随机输入变量空间样本点的随机输出变量的数据。

2）进行回归分析确定近似函数。

响应面法的基本思路是，一旦确定了这个近似函数，就可以用它来代替循环去处理有限元模型。要进行有限元分析可能需要几分钟或几小时的计算时间，而计算近似函数只需要几分之一秒的时间。因此，使用近似函数，就可以对响应参数进行成千上万次的计算。

对于工程分析来说，通常二次项就够用了。例如，评价热应力、弹性模量和热膨胀系数对热应力的影响是线性的，在平方近似中使用混合项就可以模拟。但是，有些情况下二次近似是不够的，例如，有限元结果是用来计算零件的寿命，在这种情况下，寿命通常是输入变量的指数关系，因此使用二次近似就不行了。但是，如果使用对数变换后，这些数据就一可以用二次近似来模拟了。ANSYSPDS提供了几个变换函数，可以用于响应变量，对数变换函数是其中之一。

假设近似函数是符合要求的，那么响应面法有如下优势。

●通常比蒙特卡罗模拟技术需要的循环次数少。

●可以进行非常低概率的分析，这是蒙特卡罗模拟技术一般不能实现的，除非蒙特卡罗模拟技术进行非常大量的分析循环。

●拟合系数表示近似函数的可靠程度，或者说表示与实际响应数值的近似程度。拟合系数能够在近似函数精度较差时提醒用户需要重新定义。

●单个循环之间是互相独立的（一个循环的结果不会影响另外一个），这使得响应面法非常适合于并行处理。

响应面法有如下缺点。(www.daowen.com)

●需要的循环次数取决于随机输入变量的个数。如果有很多随机输入变量（几百个或几千个），那么使用响应面法就不太现实了。

●不适用于随机输出变量与随机输入变量的函数不平滑的情况，例如，当随机输入变量变化不大的情况下随机输出变量的数值有了一个突变，这通常在模型中有不稳定的情况时（如失稳）出现。同样，当模型中有变化很大的非线性（如理想弹塑性材料）时也会出现这种情况。如果进行接触分析，随机输入变量很小的变化都可能改变接触状态，这样在使用响应面法时可能会遇到问题。

注意：要使用响应面法，随机变量间的函数关系必须是光滑连续的。如果不满足这个情况，不要使用这种方法。

2.中心合成设计抽样

中心合成设计抽样（简称CCD抽样）包括一个中心点、N个轴线点和位于2^N-f阶乘个N维超立方体的顶点。这里，N是随机输入变量的数目，f是中心合成设计阶乘因子表达式中的一个参数，当为0时称做完全分解设计，为1是半分解设计，其他依次类推。随着随机输入变量数目的增加，PDS将会逐步增大阶乘因子参数f，这样始终确保仿真循环数目总是合理的。程序总是自动计算阶乘因子f的数值，所以V分解设计总是需要的，并且由于其近似函数的二次项之间并不存在任何界限和关联，从而确保在评估二次项系数时获得非常合理的精度。

如图30-14所示是一个有3个随机输入变量的CCD抽样样本点位置示意图。

使用响应面法中的中心合成设计抽样，选择菜单Main Menu|Prob Design|Prob Method|Response Surface，选择Centxl Composite选项。

3.Box-Behnken矩阵抽样

Box-Behnken矩阵抽样包括一个中心点和N维超立方体的每边中心点。如图30-15所示是3个随机输入变量的Box-Behnken矩阵抽样样本点位置示意图。

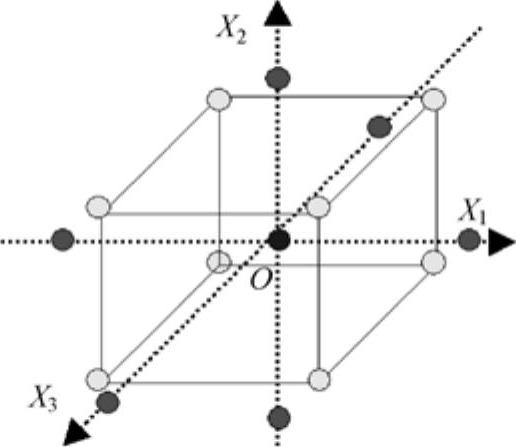
图30-14 有3个随机输入变量的CCD抽样样本点位置示意图

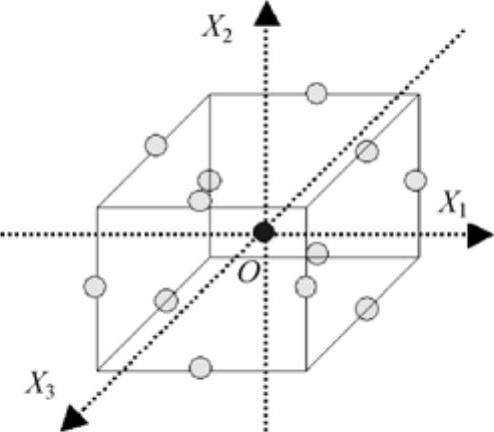
图30-15 有3个随机输入变量的Box-Behnken抽样样本点位置示意图

使用响应面法中的中心合成设计抽样，选择菜单Main Menu|Prob Design|Prob Method|Response Surface，选择Box-BehnkenMtrx选项。

下面给出一个实例，通过实例可以帮助读者掌握可靠性分析的流程和注意事项。