1.蒙特卡罗模拟技术概述

蒙特卡罗模拟技术是概率分析中最常用的传统方法，它能清楚地模拟实际问题的真实行为特征。一个仿真循环代表一个加工制造的零件，该零件承受一个特定系列的载荷和边界条件的作用。在ANSYS中，蒙特卡罗模拟技术可以选择直接抽样法或拉丁方法进行抽样处理。

在实际零部件产品制造中，当加工完一个零件后就可以测量它的几何尺寸和所有材料特性（直接在零件上测试材料特性会破坏零件，所以实际情况下一般不会直接在零件上测量）。接着，当开始使用零件进行工作时，就可以测量出它的工作载荷（要实际测得工作载荷通常也不是很容易进行的）。无论如何至少需要一个加工制造的零件并投入使用，该零件的所有输入参数都具有确定的数值（它们都是可以实际测量得到的）。同样，对于下一个制造加工的零件，同样可以重复上述过程。此时，如果将当前零件与前一个零件的参数进行比较，将会发现它们之间是存在细微差别的，这就说明输入参数其实是离散性分布的。蒙特卡罗模拟技术就是用于模拟这种制造过程中，批量生产零件各种参数的随机性问题。

其优点如下。

1）基于上述理由，蒙特卡罗模拟是概率设计基准和有效性验证的惟一适合的方法。

2）蒙特卡罗模拟过程中，每个独立循环仿真是毫不相关、完全独立的，任何一组仿真循环也完全与其他组仿真循环结果毫不相关。正因如此，蒙特卡罗模拟非常适合于采用并行计算方法。

2.直接抽样

直接蒙特卡罗抽样（简称直接抽样法）是蒙特卡罗模拟技术中最常用的基本方法，可以直接用于模拟各种工程的真实过程，非常便于理解和使用。此时，可以模拟零件在现实中的任何行为，一个仿真循环代表该零件在某个特定载荷系列作用下的行为。

直接抽样方法并不是最有效的方法，其缺点之一是需要大量的循环，因此效率不高。但是，该方法还是被广泛接受并得到使用，特别用于抽样基准和有效性验证方面，但就其缺点需要做大量的仿真循环，有些时候不容易做到。

该方法的另外一个缺点是，对抽样过程没有“记忆”功能。例如，假设有两个随机输入参数X和XZ，服从均匀分布，分布范围为0～1。利用该方法生成15个样本，可能会得到两个（或更多）集中的数据，如图30-12所示，特别是圆圈标注的两个数据。一旦出现随机输入参数采样点的集中问题，如样本中数据分布并不均匀地分布于整个输入参数的空间上，那些集中的数据点在仿真循环中相当于重复计算，此时并不能提供任何更多的有效参考价值。

使用直接蒙特卡罗模拟技术，选择菜单Main Menu|Prob Design|Prob Method|MonteCarlo Sims，再选择直接抽样法，该方法需要指定随机输入参数的样本种子值、指定仿真循环的次数和循环终比（均值和标准方差精度等）准则。

3.拉丁超立方抽样

拉丁超立方抽样（简称LHS抽样法）技术比直接抽样法更先进、更有效。LHS抽样法和直接抽样方法的唯一区别是，LHS抽样法具有抽样“记忆”功能，可以避免直接抽样法数据点集中而导致的仿真循环重复问题。同时，它强制抽样过程中抽样点必须离散分布于整个抽样空间，如图30-13所示。正因如此，在一般情况下相同问题要得到相同精度的结果，LHS抽样法比直接抽样法要少20%～30%的仿真循环次数（至于循环次数的多少，不是人为指定的，而是由问题本身决定的）。

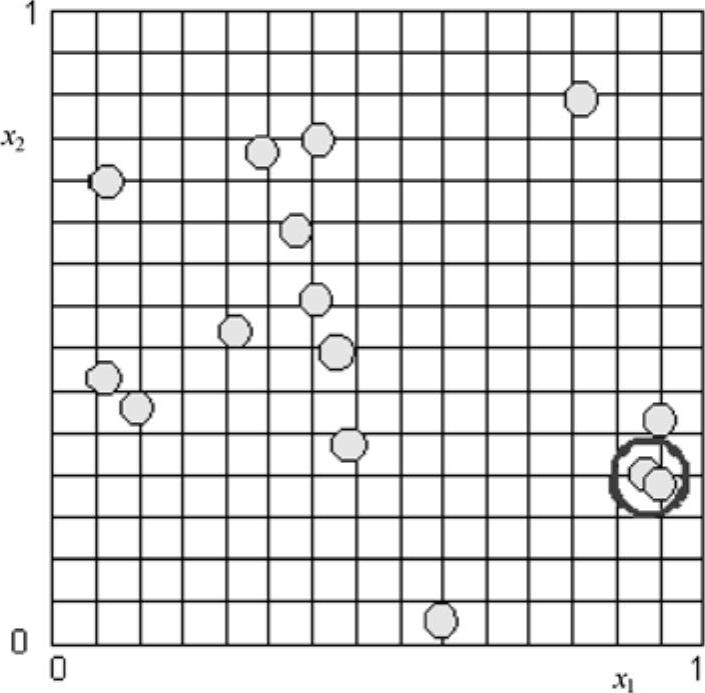
图30-12 x1和x2有两个非常接近的样本数据点

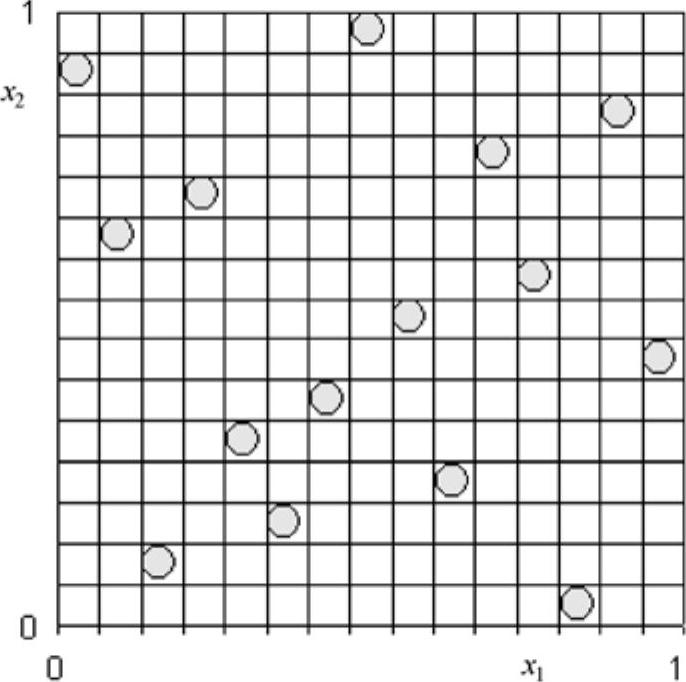
图30-13 x1和x2的样本数据点分布比较合理

使用LHS抽样法，选择菜单Main Menu|Prob Design|Prob Method|Monte Carlo Sims，再选择LEIS抽样法。该方法需要指定仿真循环次数、重复次数、样本分布位置、终止循环的准则（均值和标准方差精度）和随机输入参数样本种子值。(www.daowen.com)

4.用户定义抽样

用户定义抽样意味着样本由用户自己提供，ANSYS程序并不根据问题进行样本自动计算。用户自定义方法必须准备一个抽样数据文件，它包含所需的样本，其内容格式是一个二维数值矩阵，列数据代表定义的随机变量数目，行数据代表需要的循环次数。数据必须是ASCII码格式，具体格式要求如下。

●列分隔符可以使用空格、逗号、分号和制表符（按〈Tab〉键得到）。

●多个连续的空格和制表符当做一个分隔符处理。

●不允许出现多个逗号和分号连续，例如两个逗号之间如果没有数据（即空白）则当做空列读入，从而会导致出错提醒。

●文件的第一行必须包含一个求解标识字，并且第一行不允许出现其他数据，否则将会导致出错。如果没有求解标识字，同样会导致出错。

●求解标识字仅相当于占用一个字符位置。为了保持一致性，在PDEXE命令中必须使用相同的求解标识字，如果不一致则在后处理时总是使用PDEXE命令中使用的求解标识字。PDS系统并不检查用户指定文件中的求解标识字，并假定其总是与PDEXE中的求解标识字自动保持一致。

●文件的第二行必须包含数据列的头。前三列的头分别是ITER、CYCL和LOOP；后续列的头是各个随机变量的名称。其他数据不允许出现在这一行，否则会导致出错。当无关数据列的头出现时也会导致出错。

●文件中的随机变量名称必须与GUI菜单系统中定义的随机变量名称保持一致。

●第四列到第n列是任意排序的。ANSYSPDS根据第二行中的随机变量名称确定随机变量数据的所在列位置。

●第三行及其后续行要包含迭代数、周期数和仿真循环数，然后是该循环下的随机变量数值。迭代数、周期数和仿真循环数必须分别位于第一、第二和第三列。迭代数和周期数供ANSYSPDS内部使用，此时通常填写1。循环数是一个从1到总循环数递增的数字。其他数据不能包含在这一行中，否则将会导致出错。当所需数据不全时，也会导致出错。

●随机变量数值必须与第二行中随机变量名称一一对应。

●必须至少包含一行随机变量数据。

PDS读入指定抽样文件时，首先检查该指定的文件是否存在，然后检查它的完整性和有效性。有效性检查的依据是各随机变量的分布函数类型和最小、最大边界等。当文件中随机变量数据不符合规定时，将会出错并提供错误信息。如果参数没有范围限制，那么任意数值都可以接受，例如高斯分布。除了ANSYSPDS进行的这些检查之外，用户还要确保抽样数据与分布函数的一致性。如下列数据所示是一个基于3个随机变量X1、X2和X3的抽样自定义文件的实例，总共需要进行100次仿真循环。

使用LHS抽样法，选择菜单Main Menu|Prob Design|Prob Method|Monte Carlo Sims，再选择用户自定义抽样法。