1.陀螺效应

所谓陀螺效应，就是旋转着的物体具有像陀螺一样的效应。陀螺有两个特点：进动性和定轴性。简单来说，陀螺效应就是旋转的物体有保持其旋转方向（旋转轴的方向）的惯性。

对于一个绕轴Δ旋转的结构，如果在垂直于轴Δ施加一个扰动会发生进动且会出现反力矩。这个反力矩就是陀螺力矩。陀螺力矩的轴垂直于旋转轴也垂直于进动轴。这将导致陀螺矩阵耦合了垂直于旋转轴平面上的自由度。这也导致陀螺矩阵为非对称矩阵。

2.涡动

转子正常的旋转也包含了涡动的概念。例如转子在不平衡力矩作用下，转轴发生挠曲变形，转轴以角速度ω在空间旋转，此时转轴的运动实际上是两种运动的合成。一种是转轴绕其轴线的定轴转动，转动角速度就是旋转速度ω；另一种则是变形的轴线绕其静平衡位置的空间回转，回转角速度仍然是ω。后一种回转运动就是涡动。这就像小孩玩跳绳一样，转轴的第一种转动犹如跳绳本身旋转，转轴的第二种转动犹如弓状的跳绳在空间回转，因此称它为弓状回转，在这里称为涡动。正常转轴的涡动角速度Ω和旋转角速度ω相等，因此称它为同步涡动。凡是同步涡动，如转轴上某一方向受拉或受压，则在旋转状态下将始终受拉或受压。但是当转子发生自激振动时，由于涡动转速与转子转速不符，将发生异步涡动。如果涡动的运动方向与旋转方向相同，称为正向涡动（FW），反之则为反向涡动（BW）。不论是正向涡动还是反向涡动，转轴上某一方向将交替受拉或受压，即转子在转动状态下转子上高点位置周期性顺转向或逆转向移动。显然，当涡动速度低于转子转速时，转子上高位置将逆转向移动，反之则顺转向移动，移动速度为ω-Ω或Ω-ω。

3.椭圆轨迹

在大多数情况下，旋转轴上的节点稳态轨道也叫做轨迹，且是个椭圆形状。它的特点如下。

1）在局部坐标系XYZ中，x轴为旋转轴，在节点I处的椭圆由长半轴A，短半轴B和相位角ψ（PSI），定义如图24-1所示。

2）φ（PHI）定义了节点的初始位置。为了比较结构中两个节点的相位，用户要检查ψ+φ。YMAX和ZMAX分别是沿着Y轴和Z轴方向上的最大位移。

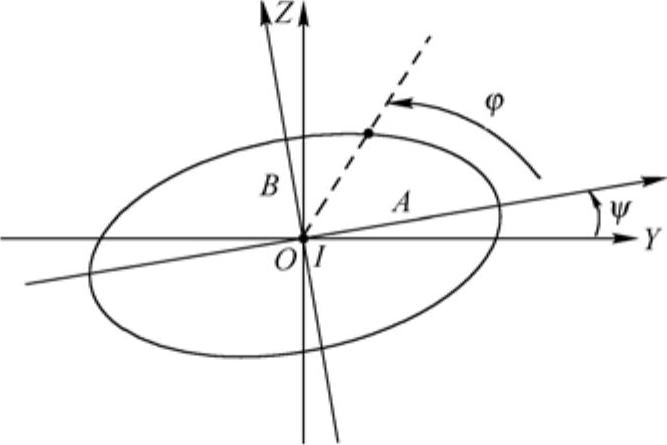
图24-1 转子的椭圆轨迹图

4.稳定性

转子保持无横向振动的正常运转状态的性能。若转子在运动状态下受微扰后能恢复原态，则这一运转状态是稳定的；否则是不稳定的。转子的不稳定通常是指不存在或不考虑周期性干扰下，转子受到微扰后产生强烈横向振动的情况。转子稳定性问题的主要研究对象是油膜轴承。油膜对轴颈的作用力是导致轴颈乃至转子失稳的因素。该作用力可用流体力学的公式求出，也可通过实验得出。一般是通过线性化方法，将作用力表示为轴颈径向位移和径向速度的线性函数，从而求出转子开始进入不稳定状态的转速----门限转速。导致失稳的还有材料的内摩擦和干摩擦，转子的弯曲刚度或质量分布在两个正交方向的不同，转子与内部流体或与外界流体的相互作用，等等。有些失稳现象的机理尚不清楚。旋转结构自励的振动在一段时间内会引起振幅的增加，如图24-2所示。(www.daowen.com)

如果没有检查，旋转结构出现了不稳定状态则能够导致设备的损坏。

旋转结构的不稳定的常见原因有如下几种。

●轴承特性。

●内部的旋转阻尼（材料阻尼）。

●旋转部分和静态部件之间的接触。

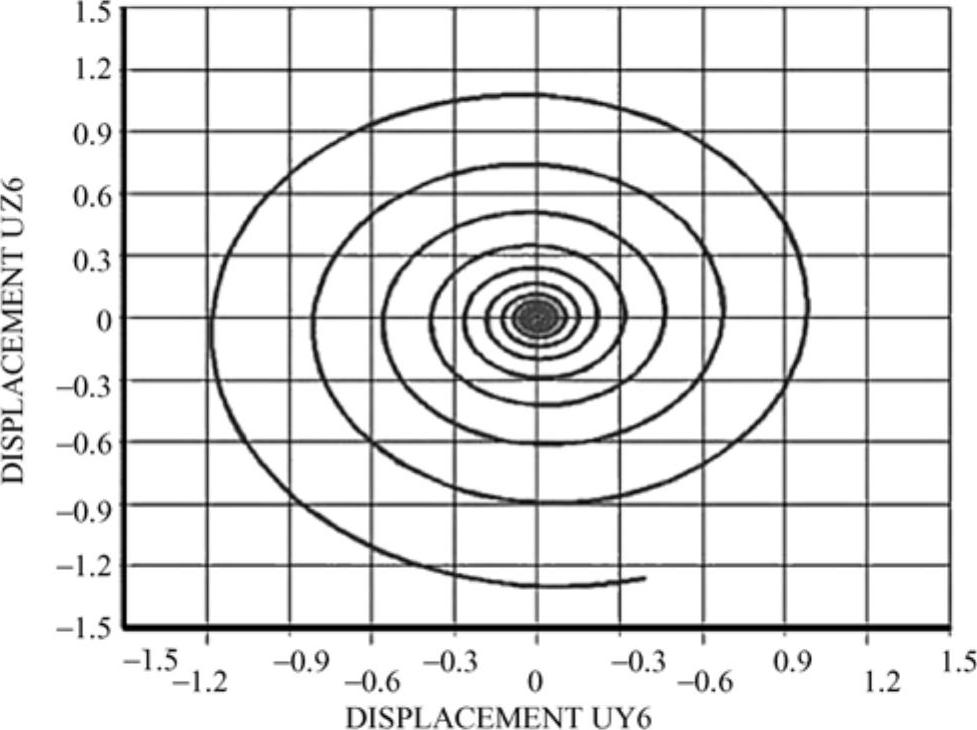
图24-2 转子中心轨迹图

5.临界转速

转动系统的转子在运转中都会发生振动，转子的振幅随转速的增大而增大，到某一转速时振幅达到最大值（也就是平常所说的共振），超过这一转速后振幅随转速增大逐渐减少，且稳定于某一范围内，这一转子振幅最大的转速称为转子的临界转速。这个转速等于转子的固有频率，当转速继续增大，接近2倍固有频率时振幅又会增大，当转速等于2倍固有频率时称为二阶（级）临界转速，依次类推有三阶、四阶。为确保机器在工作转速范围内不致发生共振，临界转速应适当偏离工作转速（例如10％以上）。

轴的临界转速决定于轴的横向刚度系数k和圆盘的质量m，而与偏心距e无关。更一般的情况是，临界转速还与轴所受到的轴向力的大小有关。当轴力为拉力时，临界转速提高，而当轴力为压力时，临界转速则降低.

通过执行坎贝尔图分析可以确定临界速度，图中频率曲线与提取转速直线的交点即为临界转速。